Zadania 3. kola
Ťavy aj vedúci vyzerali spokojne. Merlin kŕmil svoju ťavu palmovými listami zatiaľ čo Alic maturovala nad tým, ako sa nasadzuje ťave uzda, ktorá bola zmotaná v niečom, čo pripomínalo gordický uzol. Ivka na tej svojej klusala okolo a učila ju, viac či menej úspešne, parkúr. Už zdravá Anička sa nevzdávala v pokusoch vyskočiť ťave na hrb. „Koľko tie ťavy vlastne stáli?” spýtala potom, čo sa jej ani na 42. krát nepodarilo nastúpiť na ťavu. „Nepamätám si, ale ten predavač nám dal účtenku,” podával jej Macker zdrap papiera s nejakým násobením a nečitateľnými číslami.
1. príklad
Na papieri sa nachádzal príklad s klasickým násobením pod seba. Násobenie pod seba funguje tak, že násobíme horné číslo postupne ciframi toho spodného, pričom vždy keď sa posúvame na ďalšiu cifru spodného čísla, výsledok zapisujeme o jednu pozíciu viac doľava. Následne tieto medzivýpočty sčítame. Napríklad:
\begin{aligned} 12 \\ \times 34 \\ \hline 48 \\ 36 \ \ \\ \hline 408 \end{aligned}
Lenže na príklade, ktorý bol na papieri boli nečitateľné všetky cifry okrem dvoch. Príklad vyzeral takto:
\begin{aligned} ?? \\ \times ?? \\ \hline ?0? \\ 5? \ \ \\ \hline ???? \end{aligned}
Aké mohli byť čísla, ktoré násobíme? Nájdite všetky možnosti a nezabudnite vysvetliť, prečo iné možnosti už nie sú. Nezabudnite pri tom na to, že žiadne číslo sa nezačína nulou.
Konečne všetci sedeli na ťavách. Anička žmúrila striedavo na horizont a mapu, čo držala v ruke. Mapa viedla k domčeku, ktorý vyzeral, že má svoje najlepšie časy už za sebou. „Pozrite, sme skoro tu! Tu by mala bývať tá pani, čo vie, kde je poklad,” ukázala na budovu, ktorá sa svojou existenciou vysmievala statike. „Spolu s radou o poklad by sme ju mohli požiadať o použitie sprchy,” navrhla Alic, čím spustila hádku o poradie. Po chvíli to Aničku prestalo baviť a tak svojim piatim spolupútnikom rozdala kartičky s číslom poradovníka do sprchy.
2. príklad
Piati vedúci sa postavili do radu a každý z nich dostal jednu kartu. Každá karta obsahuje jedno ľubovoľné prirodzené číslo a jednu informáciu o ostatných kartách. Informácie na kartách sú nasledovné:
- Súčet čísel na všetkých ostatných kartách okrem tejto je maximálne 11.
- Súčin čísel na kartách, ktoré majú vedúci vedľa mňa, je 15.
- Mám suseda, s ktorým mám rovnaký súčin a súčet čísel na našich kartách.
- Číslo na karte človeka vľavo od tejto karty je deliteľné 5.
- Existuje karta, ktorá má číslo 4.
Zoraďte karty a každej karte priraďte prirodzené číslo, ktoré sa na nej nachádza. Nezabudnite nájsť všetky riešenia a ukázať, že žiadne ďalšie riešenia nie sú.
Otvorila im usmiata pani v bledomodrom hidžábe. Pozvala ich dnu a uvarila silný mätový čaj, do ktorého šlo takmer toľko cukru koľko vody. Pýtala sa ich na všetko možné, najviac ju zaujímalo fungovanie hromadnej dopravy na Slovensku. Po chvíli sa rozrozprávala aj ona. Keď sa pýtali na poklad, zasvietili jej oči. „Dám vám mapu, ale musíte mi sľúbiť, že ak ten poklad nájdete, donesiete mi pätinu z toho, čo ste našli.” Keďže nikto nemal námietky, po troche žmúrenia do vyrezávanej skrine vytiahla mapu. „Pozrite, tu všade bývajú moji kamaráti,” ukazovala na spleť čiar, ktoré spájali oázy.
3. príklad
Mapa vyzerala takto:

Nachádza sa tam 11 domov rôznych farieb. Každý dom je označený nejakým celým číslom. Zároveň v každom dome býva jeden kamarát. Medzi týmito domami existujú cesty, čiže čiary. Jedna cesta vždy spája práve dva domy, ako vidíte na obrázku.
Kamaráti sa chcú spolu stretávať. Lenže sú leniví a nechce sa im chodiť dlhšie ako jednu cestu. Takže dvaja kamaráti sa budú schopní stretnúť v dome, ktorý je od každého najďalej jednu cestu. To znamená, že napríklad kamarát, ktorý býva vo svetlomodrom dome sa vie stretávať s kamarátmi u seba doma, alebo vie ísť do žltého domu, alebo vie ísť do svetlozeleného domu.
Pre každú dvojicu kamarátov platí, že súčet všetkých čísel domov, kde sa vedia stretnúť, je 0. Vašou úlohou je dokázať, že ak chceme aby také niečo platilo, musia byť čísla na všetkých domoch práve 0.
Pani mala okrem vedomostí o poklade zásobu bláznivých príhod zo svojich mladých čias, až sa človek divil, že ich všetky prežila, alebo, že si ich vie tak pohotovo vymýšľať. Ževraj sa raz prihlásila na šachový turnaj, kde hrala ako živá figúrka a neskôr spomínala niečo s bojom proti černokňažníkovi. Bolo to zaujímavé a dlhé počúvanie. Veľmi dlhé. „Naozaj už musíte ísť?” pýtala sa ich s výčitkou v hlase, „To je škoda. Predtým vám ale musím povedať, ako som dláždila podlahu v princezninej kúpeľni!”
4. príklad
Majme tabuľku rozmerov 2\times5. Existuje 5 dlaždičiek s hodnotami 1, 2, 3, 4, 5. Každá hodnota je na nejakej dlaždičke práve raz. Tieto dlaždičky uložíme do horného riadku našej tabuľky v náhodnom poradí.
Dlaždičkami môžeme po políčkach tabuľky ľubovoľne hýbať tak, že nevychádzame z tabuľky, a zároveň sa dlaždičky nikdy neprekrývaju, čiže neležia jedna na druhej. Ak pohneme dlaždičku na ľubovoľné susedné voľné políčko, nazývame to ťah.
- Dokážte, že nech dlaždičky na začiatku uložíme do tabuľky v ľubovoľnom poradí, vždy ich vieme zoradiť od najmenšej po najväčšiu tak, že najmenšia je dlaždička vľavo a najväčšia je dlaždička vpravo.
- Nech sú v tabuľke 2\times5 zoradené dlaždičky 3,5,1,4,2. Koľko najmenej ťahov potrebujeme, aby sme ich zoradili do horného riadka do poradia 1,2,3,4,5? Nezabudnite dokázať, že sa použiť menej ťahov nedá.
Šťastní, že majú mapu od panej, pokračovali vedúci ďalej. Púšť okolo nich sa postupne menila z piesočnej na kamennú a po dlhej dobe šli po niečom, čo možno s trochou fantázie nazvať cesta. Na pravé poludnie sa zastavili, aby si aj oni aj ťavy oddýchli. „Poďte sa pozrieť!” zhíkla Alic pozerajúc sa do štrbiny v kameňoch. Odtiaľ na hlúčik vedúcich zízal hádam najzlatší gekon na svete a akoby na obhájenie tohto titulu si podchvíľou oblizol oči. Macker si spomenul na vombatie kocky, ktoré dostali od sfingy a postavili z nich spolu s Alic gekonovi preliezku, po ktorej sa so záujmom prechádzal.
5. príklad
Alic a Macker si postavili stavbu z 3 červených, 3 žltých a 3 zelených kociek, ktorá vyzerala ako na obrázku. Stavbu si odfotili na čiernobiely röntgenový fotoaparát a následne ju rozobrali. Fotka vyzerala takto:
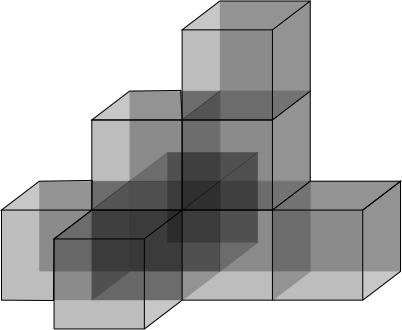
Vy by ste chceli túto stavbu postaviť znovu, no aby ste to nemali také jednoduché, vedúci vám o nej povedia len čiastkové informácie. Zároveň sa Alic a Macker dohodli, že jeden z nich vám bude klamať, takže všetky informácie ktoré vám povie budú nepravdivé. Lenže vy neviete, kto z nich vám klame. Vedúci vám povedali toto:
Alic:
- Keď som sa pozerala na stavbu zozadu, tak žiadnej farby som nevidela viac ako červenej.
- Keď som sa pozrela na stavbu zľava tak vyzerala takto:

Macker:
- Keď som sa pozrel na stavbu sprava, tak som videl 2 červené kocky.
- Keď som sa pozrel na stavbu spredu, tak vyzerala takto:

Vy ste sa teda s týmito všetkými informáciami pokúšali stavbu postaviť, no nedarilo sa vám to. Dokonca ste počítali aj s tým, že vám jeden z nich klame. Preto ste požiadali o pomoc Ivku. Ivka vám povedala takúto pravdivú informáciu:
“Ak by ste sa ma spýtali na ľubovoľnú kocku, ktorú vidíte z ľubovoľnej strany, a ja by som vám pravdivo povedala, akej je farby, stále by ste nevedeli stavbu postaviť.”
S informáciou od Ivky sa už stavba postaviť dá. Vašou úlohou je zistiť, ako vyzerá.
Gekonovi sa očividne vombatie kocky veľmi zapáčili. Potom, čo ho z nich Macker dvakrát zhodil a potom, čo na ne gekon dvakrát vyliezol, vedúci jednohlasne odhlasovali, že ho berú so sebou. Veď napokon, človek nikdy nevie, kedy sa mu zíde jeden plaz naviac. Pokračovali teda aj s ním ďalej podľa mapy. Tesne pred miestom, kde sa mal údajne vyskytovať poklad, stretli pána s detektorom kovov. Mal zahnutý klobúk a sústredene sa pozeral do zeme. Na pozdrav reagoval ešte sústredenejším pohľadom na kamene, po ktorých kráčal. Po chvíľke pozerania si Alic všimla, že stále chodí vnútri akéhosi rovnobežníka.
6. príklad
Máme rovnobežník ABCD s obsahom S. Priesečník uhlopriečok rovnobežníka označme O. Bod M leží na strane DC. Priesečník AM a BD označme E a priesečník BM a AC označme F. Súčet obsahov trojuholníkov AED a BFC je \frac{S}{3}. Zapíšte obsah štvoruholníka EOFM pomocou obsahu rovnobežníka ABCD.
Keď prešli okolo pána, boli na mieste, kde mal byť údajne poklad. Zosadli z tiav a rozhliadli sa okolo seba. Krajina sa nijako nelíšila od tej, ktorou posledné dni kráčali -všade boli kamene, živoriace stromy, prach a v pozadí zvláštny pán, točiaci sa v rovnobežníku. „Gekon cez palubu!” ozvala sa Ivka. Gekon prebehol pár metrov a zastal na hŕbe kameňov. Anička prišla k nemu, aby mu zamávala na rozlúčku. Keď sa však pozrela bližšie, všimla si, že pod kameňmi je poklop, na ktorom je napísaných veľa jednotiek.
7. príklad
Poklop má tvar mriežky 2025 \times 2025, pričom v každom štvorčeku sa nachádza buď 1, alebo -1. Anička si na papier zapísala súčin všetkých čísel v prvom riadku, potom súčin všetkých čísel v druhom riadku, a tak ďalej až napokon si zapísala súčin všetkých čísel v 2025. riadku, teda si celkovo zapísala 2025 čísel. Toto isté spravila aj pre každý stĺpec. Mohlo sa Aničke stať, že súčet všetkých čísel, ktoré si zapísala, bol 0?
Vedúci sa pri odpratávaní kameňov z poklopu poriadne zapotili, no spoločnými silami sa im ich podarilo odpratať. „Kto polezie prvý?” spýtala sa nadšená Ivka, keď otvorili poklop. Vedúci sa pozerali na rebrík, ktorý zostupoval do čierno čiernej tmy. Keď Ivka videla, že sa k tomu nikto nemá, pokrčila plecami a začala schádzať dolu. Ostatným nezostávalo nič inšie, ako ju nasledovať. Po chvíli, ktorá sa zdala nekonečná, prišli do miestnosti, ktorej steny boli pomaľované zázračnými číslami.
8. príklad
Kladné celé číslo n je zázračné, ak keď pred neho môžeme napísať ľubovoľný počet hocijakých číslic, a výsledné číslo bude vždy deliteľné n. Nájdite všetky zázračné čísla.
Miestnosť bola väčšia ako čakali. Okrem prachu v nej nebolo nič vidieť. Ešte aj svetlo z baterky bolo slabšie, akoby chcelo zostať v nej, radšej ako sa utopiť v tej tmavej prázdnote. Na konci miestnosti bol odtlačený obdĺžnik, kde bolo menej prachu. Akoby tam niekedy čosi bolo. „Vyzerá to tak, že tu pred nami niekto bol,” uškrnul sa Merlin a namieril baterku na zažltnutý papier, kde boli načarbané rovnice a kopa textu. Pri nich bola maličká poznámka: “Chachá! Tento text som zašifroval symetrickým kľúčom!” A tak vedúcim neostávalo nič iné, ako vylúštiť rovnice.
9. príklad
Dokážte, že neexistuje štvorica reálnych čísel a, b, c, d, pre ktoré platí:
„Hmmm, to nedáva zmysel,” vyhlásil Danko po dešifrovaní. Na papieri bolo napísané: Dobrý deň. Poklad bol premiestnený do Britského múzea v Londýne. Keďže ste ale prišli až sem, máte u nás vstupné zadarmo. „Tak to je smola,” zasmial sa Danko, „Ale teraz máme motiváciu spraviť si ďalší výlet!” Merlin mu neveriacky zobral papier z ruky, no nič nové na ňom nenašiel. Bol síce vystrihnutý v tvare rovnobežníka, ale Merlin usúdil, že to nebude podstatné.
10. príklad
V rovnobežníku ABCD leží bod P tak, že platí |PC| = |BC|. Dokážte, že priamka BP je kolmá na priamku, ktorá spája stredy úsečiek AP a CD.
Keď vyliezli po rebríku z miestnosti, začalo zapadať slnko. „Ak by som mala celú tú cestu za pokladom absolvovať znovu, kvôli tomuto západu slnka by sa oplatila,” usmiala sa Alic. „Asi máš pravdu. Ale ja by som ten poklad stále rád zobral. Kto by išiel so mnou ukradnúť menší poklad do múzea?” spýtal sa Macker s neskrývaným nadšením. Merlin sa na neho usmial popod fúzy.