Vzorové riešenia 1. kola
1. príklad
Najprv sa pozrieme na prípad, kedy máme 7 vedúcich. Nakreslíme si sedem miest do kruhu a budeme ich postupne vypĺňať číslami. Dôležité je uvedomiť si, že je jedno kde začneme s vypĺňaním a ktorým číslom začneme. Je to preto, že naše riešenie budeme vždy môcť pootáčať.
Ak má medzi vedúcimi so susednými číslami byť vždy práve jeden ďalší vedúci, musia stáť objedného. Začneme postavením čísla 1, ktoré napíšeme na ľubovoľné miesto. Na jednu stranu objedno miesto napíšeme číslo 2 (po smere hodinových ručičiek od 1), na druhú stranu objedno napíšeme číslo 7 (proti smeru).

Číslo 2 máme teda umiestnené. Číslo 3, už môže byť iba objedno miesto po smere hodinových ručičiek od čísla 2, lebo na druhej strane je číslo 1.

Pre číslo 4 platí podobné ako pre číslo 3. Proti smeru od predchádzajúceho (čísla 2) nemôže byť, lebo tam už je plno, preto musí byť po smere.
Ďalej rovnako ako číslo 4 umiestníme čísla 5 a 6.
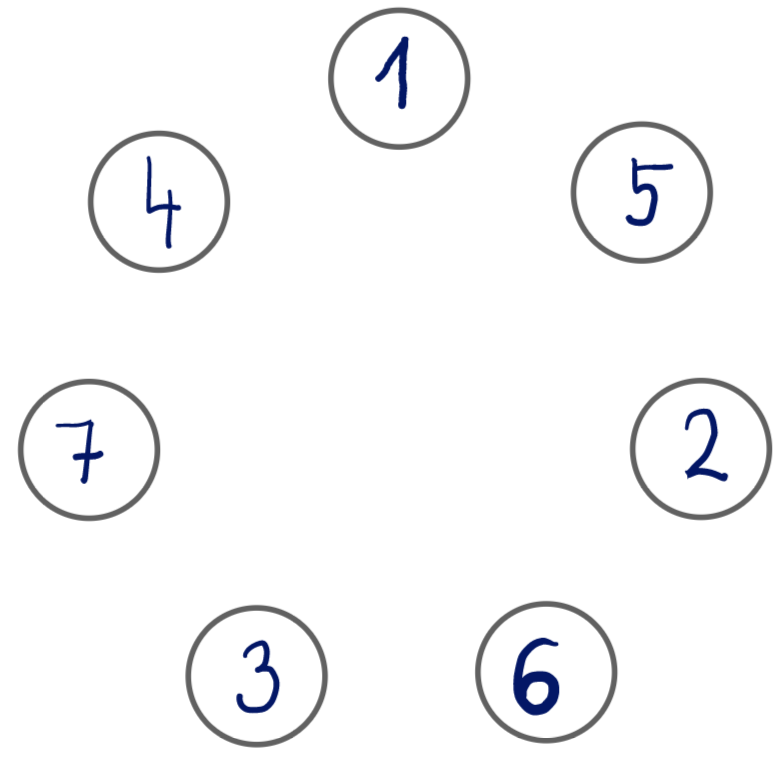
Ako posledné musíme overiť, že čísla 6 a 7 sú objedno miesto. Môžme vidieť že sú, takže tým máme prvú časť hotovú.
Podobne skúsime vypĺňať miesta, keď bude vedúcich 6. Umiestníme číslo 1 a objedno miesto susedné čísla 2 a 6. Všimnite si, že čísla 2 a 6 sú tiež objedno vedľa seba, ale tieto čísla nie sú susedné. Tiež nevieme umiestniť číslo 3 (lebo by muselo byť na rovnakom mieste ako 6 alebo 1) a ani žiadne ďalšie číslo. Kebyže začneme inak, skončili by sme v rovnakom probléme - vznikol nám tu cyklus, ktorý nejde cez všetkých 6 miest. Tým pádom pre 6 vedúcich to nie je možné.

Odpoveď:
Siedmich vedúci sa vedia postaviť do kruhu, ale šiesti to nedokážu.
Dodatok
Keďže niektorí ste sa snažili príklad riešiť všeobecne, ďalej si to len pre zaujímavosť ukážeme. Ukážeme, že to ide iba pre nepárne čísla a teda napríklad pre 7 vedúcich, ale pre 6 vedúcich nie.
Majme niekoľko miest v kruhu. Budeme ich postupne vyfarbovať. Budeme robiť niečo veľmi podobné ako predtým, len nebudeme vpisovať konkrétne čísla. Začneme na ľubovoľnom mieste, ktoré vyfarbíme na červeno. Objedno miesto (opäť po smere) vyfarbíme ďalšie miesto zelenou a budeme pokračovať vo vyfarbovaní zelenou až kým sa nebudeme blížiť k červenému miestu. Aby sme mohli pokračovať vo vyfarbovaní, musí sa nám stať, že vyfarbíme zelenou políčko hneď vedľa červeného políčka, teda aby objedno od zeleného bolo voľné.

Aby bol obrázok prehľadný, ďalej budeme pokračovať vo vyfarbovaní modrou, opäť objedno, až sa nám stane, že budeme mať vyfarbené všetky miesta.
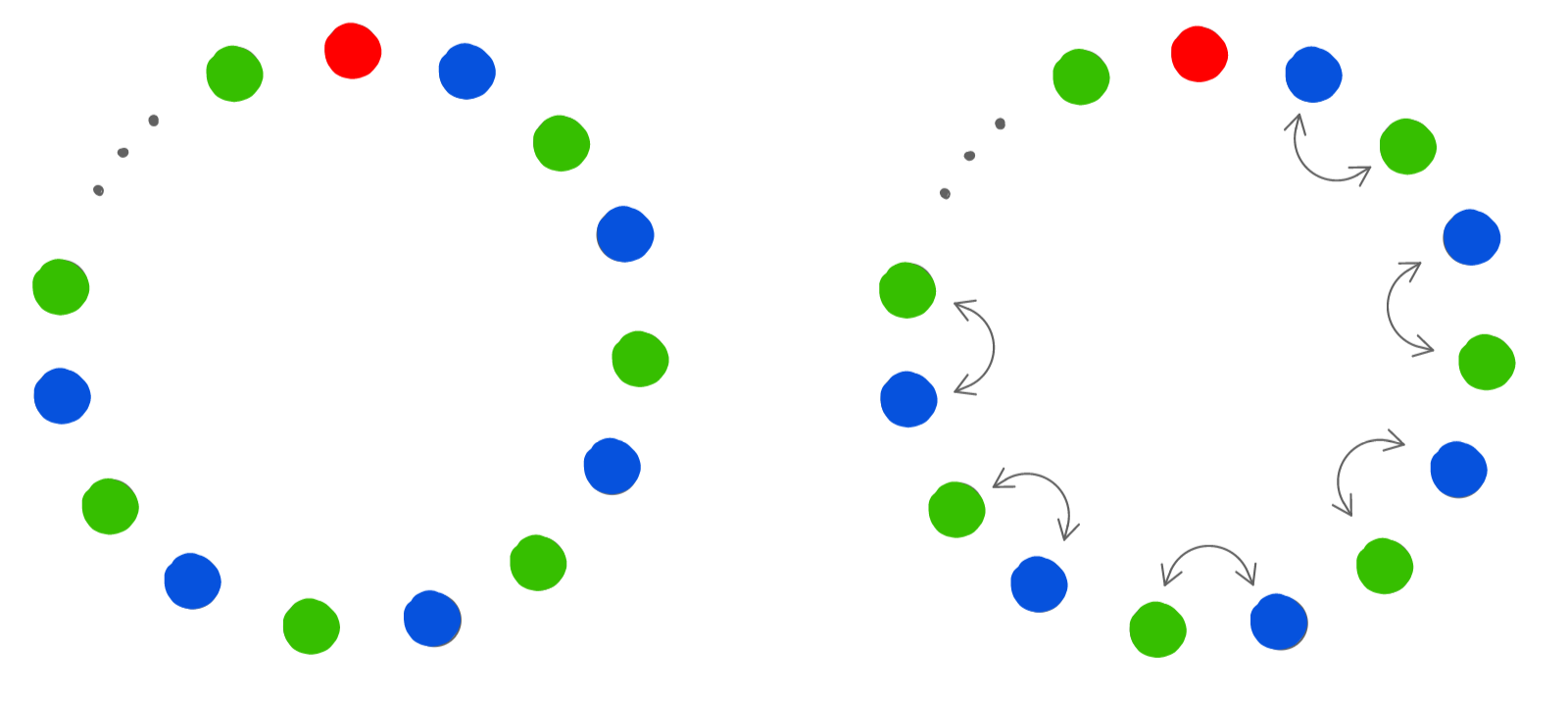
Všimnite si dôležitú vlastnosť, vždy po smere od modrého políčka sa nachádza zelené, čo znamená, že ich je rovnako veľa a teda dokopy párne veľa. Máme tu však ešte červené políčko, teda dokopy ich musí byť nepárne veľa. Tým sme ukázali, prečo to ide iba pre nepárny počet vedúcich.
2. príklad
Označme si naše hľadané 9 -ciferné číslo \overline{ABCDEFGHI}. Toto číslo je ish palindrómom, ak po pridaní číslice X na jeho začiatok, je číslo \overline{XABCDEFGHI} palindróm a zároveň po pridaní potenciálne inej číslice Y na jeho koniec je číslo \overline{ABCDEFGHIY} tiež palindrómom, teda číslom, ktoré sa číta rovnako odpredu aj odzadu. Teraz si spojíme číslice, ktoré musia byť rovnaké, aby bolo číslo \overline{XABCDEFGHI} palindróm.

Teda musí platiť, že X = I, A = H, B = G, C = F, D = E.
Ďalej spojíme číslice tak, aby bolo číslo \overline{ABCDEFGHIY} tiež palindrómom.

Teda musí platiť, že A=Y, B=I, C=H, D=G, E=F.
Vidíme, že X sa rovná číslici I, I sa rovná číslici B a tá je zas rovnaká ako číslica G … Preto všetky číslice musia byť rovnaké, a teda platí:
X=I=B=G=D=E=F=C=H=A=Y
Výsledný ish palindróm teda bude vyzerať nasledovne:
\overline{AAAAAAAAA}
A nemôže byť 0 keďže 9-ciferné číslo nemôže začínať 0, a teda máme 9 možností 9-ciferných ish palindrómov nakoľko máme 9 možností pre A:
111111111, 222222222, \dots,999999999
Podobne vieme postupovať aj pri 10-cifernom ish palindróme. Označíme si ho \overline{ABCDEFGHIJ}.
Po pridaní X na začiatok musí byť číslo \overline{XABCDEFGHIJ} palindróm.

Teda musí platiť, že X = J, A = I, B = H, C = G, D = F
Vieme, že náš ish palindróm bude palindróm aj keď pridáme číslo Y na jeho koniec. Potom získame ďalšie dvojice číslic, ktoré sa musia rovnať, aby sme získali palindróm:

Teda musí platiť, že A = Y, B = J, C = I, D = H, E = G
Čiarami sme spojili všetky čísla ktoré budú rovnaké. Môžeme si všimnúť, že pri 10 cifernom ish palindróme sa nám nespojili všetky čísla, ale len každé druhé. Vďaka tomu vidíme, že:
X=J=B=H=D=F a Y=A=I=C=G=E
Výsledný ish palindróm potom vyzerá takto:
\overline{ABABABABAB}
Cifra A nemôže byť 0, lebo inak by číslo nebolo 10-ciferné. No ani cifra B nemôže byť 0, lebo keby bola nula, tak A bude určite rôzne od B, teda pôvodné číslo nebude palindróm a taktiež po pridaní cifry 0 na začiatok sa číslo nezmení, teda to stále nebude palindróm. Napríklad číslo 1010101010 nie je ish palindróm, lebo by sme dostali číslo 01010101010 a to by začínalo 0, čo nie je možné.
Dokopy máme teda 9 možných cifier na miesto cifry A a 9 na miesto cifry B. Pre každú jednu cifru A máme teda 9 možností pre cifru B a keďže je 9 možných cifier A, tak dokopy existuje 9\cdot9=81 možností pre 10-ciferný ish palindróm:
1111111111, 1212121212, 1313131313,........,9999999999
Odpoveď:
99-ciferných ish plaindrómov je 9999999
10-ciferných ish plaindrómov je 81
3. príklad
Táto úloha sa dala riešiť viacerými spôsobmi. Tu ukážeme dva z nich.
Riešenie cez deliteľnosť
Keďže \frac{2}{7} účastníkov pozerajú do mobilu, počet účastníkov musí byť deliteľný 7. Ak by to tak nebolo, počet účastníkov pozerajúcich do mobilu by bolo desatinné číslo, čo nemôže byť. Ak by bolo účastníkov viac ako 63, bolo by im vidno viac ako 63\cdot \frac{5}{7} =45 hláv. Keďže ale hláv vidíme dokopy len 45, toto nemôže nastať.
Stačí teda rozobrať možnosti, kde je počet účastníkov násobok sedmičky od 0 do 63.
Počet hláv, ktoré je účastníkom vidno ľahko zistíme tým, že vypočítame \frac{5}{7} z počtov účastníkov. Aby sme mali spolu 45 hláv, počet kobýl vypočítame ako počet hláv ktoré je vidno, teda 45, mínus viditeľné hlavy účastníkov.
Nakoniec už len stačí sčítať počet nôh účastníkov (počet účastníkov krát 2) a počet nôh kobýl (počet kobýl krát 4).
| účastníkov | vidno hláv účastníkom | počet kobýl | spolu nôh |
|---|---|---|---|
| 0 | 0 | 45 | 180 |
| 7 | 5 | 40 | 174 |
| 14 | 10 | 35 | 168 |
| 21 | 15 | 30 | 162 |
| 28 | 20 | 25 | 156 |
| 35 | 25 | 20 | 150 |
| 42 | 30 | 15 | 144 |
| 49 | 35 | 10 | 138 |
| 56 | 40 | 5 | 132 |
| 63 | 45 | 0 | 126 |
Ako vidíme z tabuľky, správny počet nôh nám vyjde jedine v možnosti, že účastníkov je 21 a kobýl 30.
Riešenie cez rovnice
Označme si U= počet účastníkov, K= počet kobýl. Teraz vieme vytvoriť 2 rovnice. Jednu na počet nôh a druhú na počet hláv.
Keďže každý účastník má 2 nohy, každá kobyla má 4 nohy a spolu majú 162 nôh, tak platí:
2\cdot U+4\cdot K=162
Hlavy nevidíme \frac{2}{7} účastníkov, čo znamená, že \frac{5}{7} účastníkov ich vidíme. Každá kobyla má iba jednu hlavu a spolu je hláv 45, čím dostaneme nasledovnú rovnicu:
K+\frac{5}{7} \cdot U=45
Z druhej rovnice si nasledovne vyjadríme K. Od oboch strán odčítame \frac{5}{7} \cdot U a dostávame:
K=45-\frac{5}{7} \cdot U
To teraz dosadíme do rovnice o nohách:
162 = 2\cdot U + 4\cdot (45 - \frac{5}{7} \cdot U)
162 = 2\cdot U + 180 - \frac{20}{7} \cdot U / - 180
-18 = 2\cdot U - \frac{20}{7} \cdot U / 2\cdot U = \frac{14}{7} \cdot U
-18 = \frac{14}{7} \cdot U - \frac{20}{7} \cdot U
-18 = -\frac{6}{7} \cdot U /\cdot (-7)
126 = 6\cdot U / :6
21 = U
Počet kobýl potom už len jednoducho dopočítame:
K = 45-\frac{5}{7} \cdot U = 45 - \frac{5}{7} \cdot 21 = 45 - 15=30
Teraz už stačí len urobiť skúšku správnosti:
Rovnica o nohách: 2\cdot U + 4\cdot K = 2\cdot 21 + 4\cdot 30 = 42 + 120 = 162 SEDÍ
Rovnica o hlavách: K + \frac{5}{7} \cdot U = 30 + \frac{5}{7} \cdot 21 = 30 + 15 = 45 SEDÍ
Odpoveď:
Účastníkov bolo 21 a kobýl 30.
Komentár
Pri riešení pomocou deliteľnosti sa dá veľmi jednoducho zabudnúť, že účastníkov môže byť aj 0. Stále však treba preskúmať aj túto možnosť.
4. príklad
Zo zadania vieme, že čísla v každom riadku, stĺpci, aj uhlopriečke majú súčin 216 . To znamená, že všetky čísla v tabuľke musia byť deliteľmi 216 . Najlepší spôsob na nájdenie všetkých deliteľov je pomocou prvočíselného rozkladu čísla 216 , čo je 2\cdot2\cdot2\cdot3\cdot3\cdot3=216 . Z týchto čísel vieme potom postupne vyskladať všetky delitele čísla 216 , a to 1 , 2 , 3 , 4, 6, 8, 9, 12, 18, 24, 27, 36, 54, 72, 108, 216. Každé z týchto čísel vzniklo nejakou kombináciou dvojok a trojok z prvočíselného rozkladu a okrem toho je na zozname ešte 1 a 216.
Týchto deliteľov je ale viac ako miest v tabuľke. Niektoré z nich teda nebudú vyhovovať riešeniu. Ako zistíme, že ktoré v tabuľke budú a ktoré nie? Ak sa pozrieme na jednotlivé miesta v tabuľke, vidíme, že každé sa nachádza práve v jednom riadku a jednom stĺpci. Preto musia pre každé číslo, ktoré bude v tabuľke, existovať aspoň dve trojice deliteľov 216, ktorých súčin je 216 (jedna pre riadok a druhá pre stĺpec). Číslo v rohu tabuľky leží naviac aj na jednej uhlopriečke, preto musí byť v troch trojiciach. No a číslo v strede tabuľky leží na oboch uhlopriečkach, preto bude až v 4 trojiciach (pozri obrázok).

Vidíme teda, že na to, aby mohlo byť číslo v tabuľke, musí spĺňať nejakú podmienku - byť aspoň v dvoch trojiciach deliteľov, s ktorými bude v riadku a stĺpci, prípadne na uhlopriečkach. Pozrime sa v akých trojiciach sa nachádzajú najväčšie delitele čísla 216:
| 216 | 216 | len jedna trojica, nevyhovuje |
| 108 | 108\cdot2\cdot1 | len jedna trojica, nevyhovuje |
| 72 | 72\cdot3\cdot1 | len jedna trojica, nevyhovuje |
| 54 | 54\cdot4\cdot1 a 54\cdot2\cdot2 | v druhej dvojici sa opakujú čísla, nevyhovuje |
| 36 | 36\cdot6\cdot1 a 36\cdot3\cdot2 | vyhovuje |
Do ktorého políčka ho ale dáme? Vieme, že nemôže byť v rohových, keďže rohové číslo musí mať aspoň tri trojice. Preto bude v prvom riadku v strede. Ostáva nám umiestniť čísla 1, 2, 3, 6. Aby sa nám lepšie opisovali kroky, je výhodné označiť si tieto políčka A, B, C a D.
A | 36 | B |
C | ||
D |
Ak sa budeme s tabuľkou chvíľku hrať a skúšať si tam dopĺňať aj ďalšie čísla, všimneme si, že akonáhle sa v jednom riadku, stĺpci alebo uhlopriečke nachádza 1 spolu s 2 alebo 3, sme nútení doplniť jedno z čísel 108 alebo 72, ktoré sme si už ukázali, že v tabuľke byť nemôžu.
1 bude preto na políčku D, keďže to je jediný spôsob ako sa vyhneme číslam 72 a 108, potom číslo 6 bude na políčku C a na políčkach A a B budú čísla 2 a 3 (A=2 a B=3 alebo A=3 a B=2 sú rovnaké možnosti, len zrkadlovo otočené, na to netreba zabudnúť).
2 | 36 | 3 |
6 | ||
1 |
Ďalej už do tabuľky bez problémov vieme doplniť ostatné políčka, keďže každé doplnenie je už jednoznačne dané. Vľavo dole bude 12, vpravo dole bude 18, v strede vľavo bude 9 a v strede vpravo bude 4. Takto máme už vyplnenú celú tabuľku.
Týmito dvoma spôsobmi sa dá tabuľka vyplniť tak, aby boli splnené podmienky zo zadania:
2 | 36 | 3 |
9 | 6 | 4 |
12 | 1 | 18 |
Alebo zrkadlovo prevrátené:
3 | 36 | 2 |
4 | 6 | 9 |
18 | 1 | 12 |
Iné riešenie
Ďalší spôsob ako pristupovať k príkladu je pozerať sa na tabuľku ako na sadu neznámych čísel, ktoré si opäť môžeme označiť písmenkami. Keďže zo zadania vieme, že súčin v každom riadku, stĺpci aj uhlopriečke je 216, hneď nám napadne si z toho vytvoriť rovnice. Tak ako v tomto prípade, väčšinou sa oplatí pozrieť sa na tie rovnice, kde sa najviac opakuje jedno písmenko, v tomto prípade E (sú až štyri.).
A | B | C |
D | E | F |
G | H | I |
B \cdot\ E \cdot\ H = 216
D \cdot\ E \cdot\ F = 216
A \cdot\ E \cdot\ I = 216
C \cdot\ E \cdot\ G = 216
Teraz sa budeme snažiť rovnice zjednodušiť, aby sme z nich vedeli niečo vyčítať. Preto medzi sebou vynásobíme ľavé strany a pravé strany. Vyjde nám nasledovná rovnica:
(B \cdot\ E \cdot\ H)(D \cdot\ E \cdot\ F)(A \cdot\ E \cdot\ I)(C \cdot\ E \cdot\ G) = 216 \cdot\ 216 \cdot\ 216 \cdot\ 216
Keďže ide o násobenie, môžeme si zátvorky odmyslieť a písmenká preusporiadať nasledovne:
(A \cdot\ D \cdot\ G)(C \cdot\ F \cdot\ I)(B \cdot\ E \cdot\ H)(E \cdot\ E \cdot\ E) = 216 \cdot\ 216 \cdot\ 216 \cdot\ 216
Za prvé tri zátvorky dosadíme 216, keďže ide o stĺpce z tabuľky a vykrátia sa nám:
216 \cdot\ 216 \cdot\ 216 \cdot\ (E \cdot\ E \cdot\ E) = 216 \cdot\ 216 \cdot\ 216 \cdot\ 216 / : (216 \cdot 216 \cdot 216)
(E \cdot E \cdot E)=216
Kedže vieme že E je reálne kladné číslo tak môžeme z oboch strán spraviť 3. odmocninu a dostaneme
E=6
Z týchto úprav sme zistili, že v strednom políčku bude určite 6.
Teraz sa pokúsime zistiť najväčšie číslo, ktoré vieme dať do prvého riadku.
Keď už vieme presnú hodnotu E, dosadíme si E=6 do predošlých rovníc. Z toho nám výjdu tieto rovnice:
A \cdot\ 6 \cdot\ I = 216 / :6
A \cdot\ I = 36
B \cdot\ 6 \cdot\ H=216 / :6
B \cdot\ H=36
C \cdot\ 6 \cdot\ D=216 / :6
C \cdot\ D = 36
Teraz sa pozrieme na to, čo nám z týchto rovníc vyplýva. Vieme zistiť, že políčka A,I,B,H,C,D sú menšie rovné 36. (Ak by bolo niektoré políčko väčšie, určite by aspoň jeden zo súčinov A\cdot I, B \cdot H a C\cdot D bol väčší ako 36.)
Preto medzi políčkami A, B, C (tie sú v prvom riadku) bude najviac 36. Poďme s ním vyskúšať doplniť celú tabuľku. Ak nám to vyjde, máme určite správne riešenie a splnené podmienky zo zadania.
Vieme, že 36 je deliteľom 216, lebo v predošlých krokoch sme si už ukázali, že 6x36=216. Prvočíselný rozklad 6 je 2 \cdot3. Preto vieme, že jediné dve trojice, ktorých súčin je 216 a obsahujú 36 sú: 1\cdot6\cdot36 a 2\cdot3\cdot36.
Teraz zistíme, kde sa môže 36 nachádzať. 36 nemôže byť v rohovom políčku, pretože je súčasťou len dvoch trojíc. Na to, aby mohla byť v rohovom, musí byť súčasťou aspoň troch, v riadku, stĺpci aj uhlopriečke. Tým pádom musí byť v strednom. To znamená, že B=36.
2 | 36 | 3 |
D | 6 | F |
G | 1 | I |
Ďalej už do tabuľky bez problémov vieme doplniť ostatné čísla tak, ako v predošlom riešení.
5. príklad
Dôležitá vec, ktorú si na začiatok môžeme všimnúť je, že celkový počet hlasov sa mení podľa toho, koľko ľudí má a koľko nemá družinku (pre každého, čo nemá družinku je o jeden hlas viac).
V príklade nás zaujíma, že kedy je hlasovanie jednoznačné, takže sa pozrime najprv na to, hlasovanie je jednoznačné, keď sa v skupinke hlasy nevedia rozdeliť na dve polovice s rovnakým počtom hlasov. Napríklad sa nevedia rozdeliť keď je niekto sám, alebo je celkový počet hlasov v skupinke nepárny.
Teraz by bolo pekné vedúcich rozdeliť na 2 takéto skupinky. Toto by pekne vyšlo ak by sme pri párnom súčte hlasov odobrali jedného s nepárnym počtom a pri nepárnom počte jedného s párnym počtom hlasov, tieto prípady si teda môžeme rozobrať detailnejšie:
Keď je celkový počet hlasov párny, tak si uvedomíme, že musí existovať vedúci s jedným hlasom, lebo ak by neexistoval, tak každý vedúci by musel mať aspoň dva hlasy, teda keďže je celkovo 6 vedúcich tak by muselo byť najmenej 12 hlasov a teda 12 družiniek, čo je v rozpore so zadaním.
Potom vieme dať vedúceho s jedným hlasom do jednej skupinky. Keďže celkový počet hlasov je párny a do jednej skupinky sme dali vedúceho s nepárnym počtom hlasov, tak v druhej bude počet hlasov tiež nepárny a teda hlasovanie bude vždy rozhodné.
Keď je celkový počet hlasov nepárny, tak si uvedomíme, že musí existovať vedúci s párnym počtom hlasov, lebo ak by mal každý vedúci nepárny počet hlasov, tak keďže je ich 6 tak by celkový počet hlasov bol párny (párny\ počet\ vedúcich \cdot nepárny\ počet\ hlasov\ každého = párny\ súčet), a to sme už vyššie vyriešili.
Potom vieme dať vedúceho s párnym počtom hlasov samého do skupinky, a keďže celkový počet hlasov je nepárny, tak v druhej skupinke bude počet hlasov nepárny, a teda hlasovanie bude vždy rozhodné.
Odpoveď:
Vieme vždy rozdeliť vedúcich do dvoch skupiniek, tak aby bolo vždy rozhodné hlasovanie v oboch skupinkách.
6. príklad
Túto úlohu niektorí z riešiteľov pochopili tak, že je 7 \times 7 križovatiek a kraje sú od seba vzdialené 6 podchodov. Zamýšľané, bolo že je 6\times6 križovatiek a kraje sú vzdialené 5 podchodov. Keďže zadanie v tomto nebolo úplne jasné a riešenie sa hľadalo rovnako v oboch veziách, obe sme nakoniec uznávali ako správne. Vo vzorovom riešení sa však pozrieme iba na tú prvú, postupne po podúlohách.
Podúloha a)
V tejto podúlohe môžme navrhnúť podchody napríklad tak ako na obrázku, že cez všetky križovatky pôjde slučka. Je jedno, ako nasmerujeme ostatné podchody, všade sa dá dostať ak pôjdeme po tejto slučke.
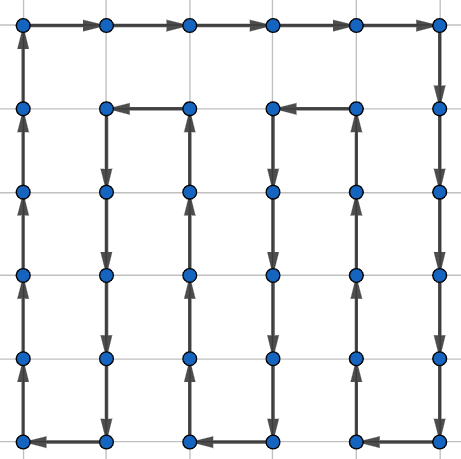
Podúloha b)
V tejto podúlohe išlo o to, či sa vždy, keď z každej križovatky vychádza aj vchádza podchod, dá dostať odvšadiaľ všade. Ak by teda existovalo rozmiestnenie, kde síce z každej križovatky vychádza aj do každej vchádza podchod, ale nedá sa dostať odvšadiaľ všade, odpoveď na b) bude nie. Jedno z takých rozmiestnení je to na obrázku. V tomto rozložení síce z každej križovatky vychádza podchod aj do každej vchádza, ale z hornej polovice obrázka sa do dolnej nedá dostať.
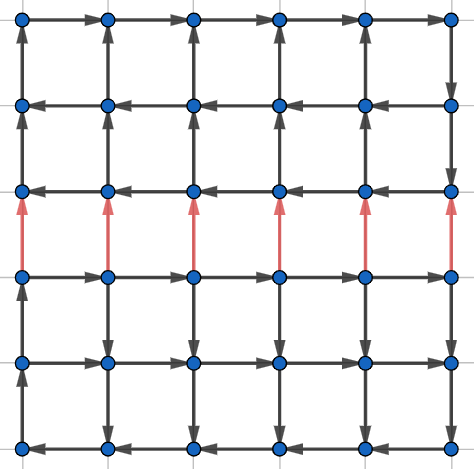
Podúloha c)
Na to, aby sme vždy prešli cez najviac dva zbytočné podchody je možné použiť napríklad rozloženie na obrázku. Bolo ale naozaj ťažké nájsť toto alebo iné správne riešenie a dokázať jeho správnosť bez manuálnej kontroly veľkého množstva ciest. Preto sme sa nakoniec rozhodli nedávať za túto podúlohu body a namiesto toho dať viac bodov za ostatné podúlohy.

Podúloha d)
Potrebujeme zistiť, či sa podchody dajú navrhnúť s podmienkou, že sa všade dá dostať na jeden zbytočný podchod. Najprv sa zamyslime, či nejakú časť rozmiestnenia nevieme určiť naisto, takú bez ktorej by rozmiestnenie isto nespĺňalo podmienku. Je jasné, že z rohu musí jeden podchod vychádzať a jeden doň prichádzať. Keby totiž oba vychádzali alebo vchádzali, nedalo by sa vojsť alebo vyjsť. Je jedno, ktorý z nich bude ktorý, lebo môžme tabuľku po uhlopriečke preklopiť a dostaneme tým tú druhú situáciu. Nakreslime si teda roh s týmito dvoma podchodmi. Zároveň si označme križovatky písmenami a číslami aby sa o nich ľahšie písalo.
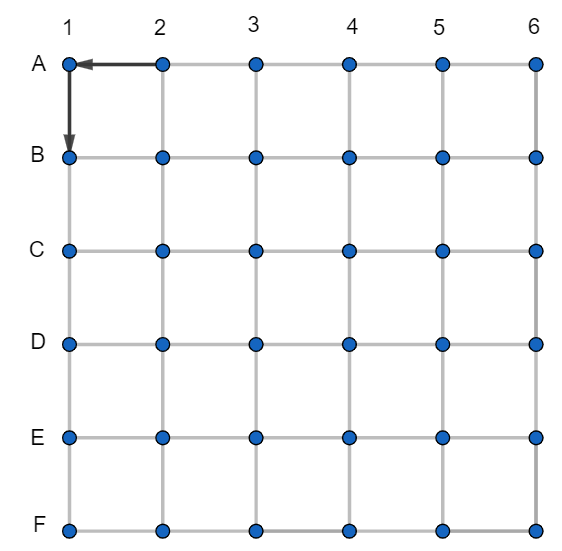
Teraz je len jedna trasa, ktorou sa dá dostať z B1 do A1 na najviac jeden zbytočný podchod - doprava, hore a doľava. Ak teda nechceme porušiť podmienku, musia tam byť podchody tak, ako na obrázku.
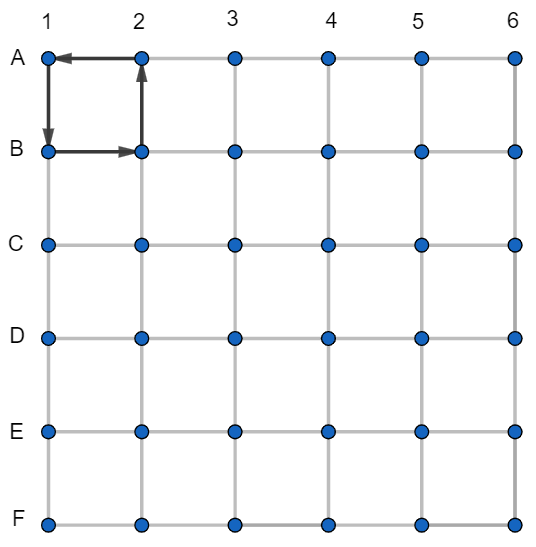
Ak by viedol podchod z B1 do C1, tak potom by sa naspäť, z C1 do B1, nedalo dostať kratšou cestou ako cez C2, B2, A2 a A1 - na dva zbytočné podchody. To by teda nebolo dobré rozloženie a tak musí viesť podchod naopak - z C1 do B1.
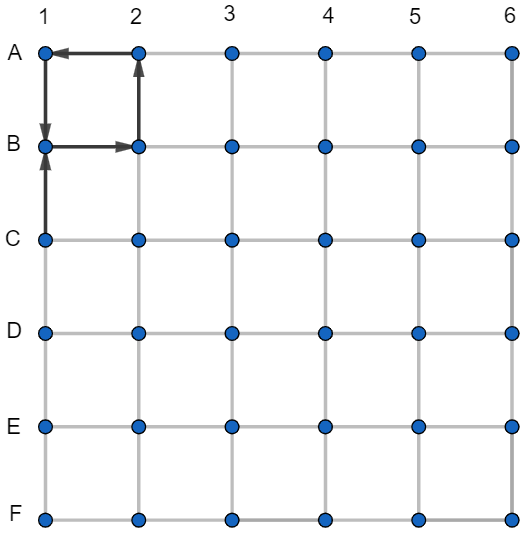
Podobne, ako pred chvíľou z B1 do A1, jediná možná cesta z B1 do C1 s najviac jedným zbytočným podchodom je cez B2 a C2, preto tam musia byť podchody ako na obrázku.
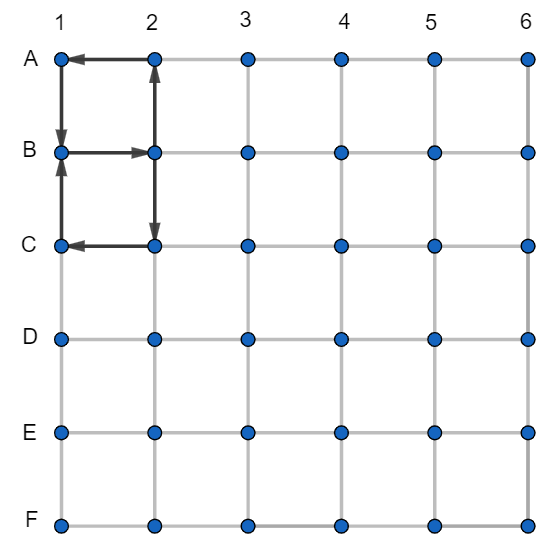
Ak by viedol podchod z D1 do C1, nedalo by sa prejsť na 1 zbytočný z C1 do D1. Preto pôjde podchod z C1 do D1.
A teraz, podobne ako už dvakrát predtým, aby sa dalo dostať z D1 do C1, musia viesť podchody takto:
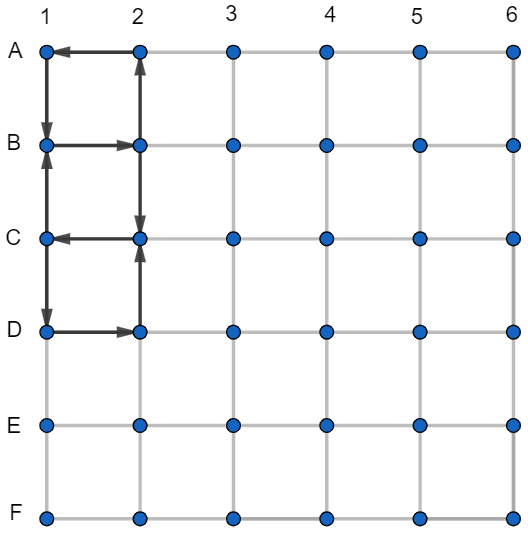
Ak by viedol podchod z D1 do E1, nedalo by sa dostať z E1 do D1 na najviac jeden zbytočný podchod. Preto musí viesť z E1 do D1.
Teraz si ale skúsme nájsť cestu z A1 do E1. V prvom kroku musíme ísť dole, v druhom doprava, čo je prvý zbytočný podchod. Ak teda chceme prejsť iba s jedným zbytočným podchodom, musíme sa odtiaľto už stále približovať. Ešte tri kroky sa nám to môže (práve jedným spôsobom) podariť - pôjdeme na C2, C1 a D1. Odtiaľ ale môžme ísť iba doprava, čím naberieme druhý zbytočný podchod.
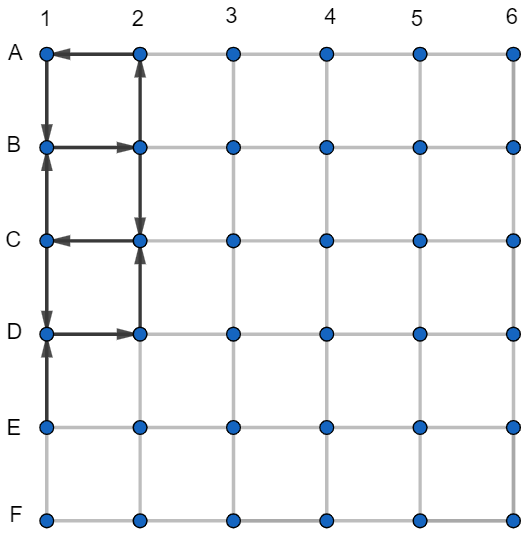
Ako sme už vysvetlili, rozloženie ku ktorému sme sa dostali, musí byť takto alebo osovo preklopené súčasťou každého rozdelenia, ktoré spĺňa podmienku v d). Aj tu však vidíme, že podmienky splnené nebudú a tak nemôžu byť splnené v žiadnom rozložení.
Odpoveď: Pre a) sme našli fungujúce rozloženie, v b) sme našli prípad, ktorý to vyvracia, c) sa urobiť dalo, a v d) sme ukázali, že sa také rozloženie nájsť nedá.
7. príklad
4 \lfloor x \rfloor = 3x.
Rozdeľme si x na časť, ktorá je celým číslom a na desatinnú časť, ktorú označme y. Takže x = \lfloor x \rfloor + y a ďalej
\begin{aligned} 4 \lfloor x \rfloor &= 3 \cdot ( \lfloor x \rfloor + y)\\ 4 \lfloor x \rfloor &= 3 \cdot \lfloor x \rfloor + 3 \cdot y &/ - 3 \lfloor x \rfloor\\ \lfloor x \rfloor &= 3y. \end{aligned}
Keďže y je desatinná časť tak vieme, že 0 \leq y \lt 1. Taktiež vieme, že \lfloor x \rfloor je celé číslo, teda aj 3y je celé číslo. Takže y bude zlomok s menovateľom 3 a celočíselným čitateľom, pretože po prenásobení 3 potom tento zlomok bude celé číslo. 3 \cdot {z \over 3} = z.
A aký môže byť celočíselný čitateľ? Vieme, že y je menej ako jedna teda z \lt 3, takže z môže byť 0, 1 alebo 2. Dosaďme teraz do rovnice y = {0 \over 3} = 0.
\begin{aligned} \lfloor x \rfloor &= 3y = 3 \cdot 0 = 0\\ 3 \cdot x &= 4 \lfloor x \rfloor = 4 \cdot 0 = 0\\ x &= 0. \end{aligned}
Rovnaký výpočet teraz spravíme aj pre y = \frac{1}{3} a y = \frac{2}{3}.
\begin{aligned} \lfloor x \rfloor &= 3y = 3 \cdot \dfrac{1}{3} = 1\\ 3 \cdot x &= 4 \lfloor x \rfloor = 4 \cdot 1 = 4\\ x &= \dfrac{4}{3}. \end{aligned}
\begin{aligned} \lfloor x \rfloor &= 3y = 3 \cdot \dfrac{2}{3} = 2\\ 3 \cdot x &= 4 \lfloor x \rfloor = 4 \cdot 2 = 8\\ x &= \dfrac{8}{3}. \end{aligned}
Odpoveď: Tri možnosti pre x spĺňajú zadanú rovnicu. Sú to x = 0, x = {4 \over 3} a x = {8\over 3} .
8. príklad
Zo zadania máme |BD| = |DA|, takže trojuholník BDA je rovnoramenný so základňou AB. Uhly pri základniach v rovnoramennom trojuholníku sú rovnako veľké, takže |\sphericalangle BAD| = |\sphericalangle ABD| = 30 \degree. Pozrime sa na uhol |\sphericalangle ADB|. Súčet vnútorných uhlov trojuholníka je 180 \degree, takže 180 \degree = |\sphericalangle ADB| + |\sphericalangle BAD| + |\sphericalangle ABD|. Po dosadení a odčítaní známych uhol dostaneme |\sphericalangle ADB| = 120 \degree. Body B, D, C ležia na priamke a teda |\sphericalangle BDC| = 180 \degree. Pre \sphericalangle BDC platí |\sphericalangle BDC| = |\sphericalangle BDA| + |\sphericalangle ADC|. Po dosadení a odčítaní známych uhlov nám ostane |\sphericalangle ADC| = 60 \degree.

Keď sa pozrieme na obrázok, čo sme zatiaľ ukázali, môžeme si všimnúť, že už viac z náčrtu nedostaneme. Teda ďalšie uhly len pomocou trojuholníkov a susedných uhlov nevieme dopočítať. Podmienku zo zadania |BD| = |DA| sme už využili. Jediné, čo nám ostáva je podmienka |BD| = 2 \cdot |DC|, z ktorej ako tak samej o sebe nevieme nič moc zistiť. Teda potrebujeme si do obrázku niečo doplniť. My si doplníme bod E taký, že E je na priamke DC, |DC| = |CE| a E je rôzny od D.
Zo zadania máme |DA| = |DB| = 2 \cdot |DC|, keďže |DC| = |CE|, tak |DA| = |DC| + |CE| = |DE|. To znamená, že trojuholník ADE je rovnoramenný so základňou AE. Teraz sa pozrime na uhly v ADE: 180 \degree = |\sphericalangle DAE| + |\sphericalangle AED| + 60 \degree. Keďže však ADE je rovnoramenný, tak neše dva neznáme uhly sú rovnako veľké a po úprave rovnosti dostaneme, že |\sphericalangle DAE| = |\sphericalangle AED| = 60 \degree.
Keďže v trojuholníku ADE sú všetky uhly rovné 60 \degree, tak ADE je rovnostranný trojuholník. Bod C je z stred úsečky DE, lebo |DC| = |CE|, takže CA je ťažnica. V rovnostrannom trojuholníku sa však ťažnica zhoduje s výškou a teda CA musí byť aj výška. To však ale znamená, že |\sphericalangle BCA| = 90 \degree.
Odpoveď: Veľkosť uhla \sphericalangle BCA je 90 \degree.
Komentár
Väčšina z vás túto úlohu riešila rovnako, ako sme popísali vo vzoráku, teda ste si doplnili E, ako bolo popísané. Rovnako sa dala úloha doriešiť aj s dokreslením stredu strany AD, spravením kolmice na úsečku AB v bode A, spravením osi strany AB. Na čo si však je treba dávať pozor pri dokreslovaní do obrázka je, či naozaj napríklad dokreslené priamky sa pretnú v správnej polrovine, alebo nejaká päta výšky leží na strane, alebo na jej predĺžení, lebo potom už vám nemusia výpočty vychádzať.
9. príklad
Na označenie skutočnosti, že a delí b používame zápis a\mid b. Naopak, ak a nedelí b, tak píšeme a\nmid b. Teda napríklad 3\mid 6 alebo 7 \mid 21, ale 2\nmid 9. Úloha 9 tak od nás požaduje, aby sme našli všetky celé n \geq 6 také, že n\mid (n-4)!.
Overme najprv prípady, kedy n\in \{ 6,7,8,9 \}. Pre n=6 dostávame (n-4)! = 2! = 2 a zrejme 6 \nmid 2, preto n=6 nevyhovuje. Pre n=7 dostávame (n-4)!=3!=6, avšak opäť platí 7\nmid 6, teda ani n=7 nevyhovuje. Pre n=8 máme (n-4)!=4!=24, a keďže platí 8\mid24, tak vidíme, že n=8 vyhovuje. A nakoniec ak n=9, tak (n-4)!=5!=120, avšak 9\nmid 120, a teda n=9 úlohe nevyhovuje. Po zvyšok riešenia tak uvaužjme iba n\geq 10.
Všimnime si najprv, že ak by n=p bolo prvočíslo, tak potom aby platilo p\mid (p-4)!, muselo by sa prvočíslo p nachádzať v prvočíselnom rozklade čísla (p-4)! = 1\cdot 2 \cdot 3\cdot \ldots \cdot (p-4). To znamená, že prvočíslo p by sa však muselo nachádzať aj v prvočíselnom rozklade aspoň jedného z čísel 1, \ 2, \cdots, p-4. To je však nemožné, keďže p je väčšie ako každé z nich.
Ostáva tak vyriešiť prípad, kedy n\geq 10 je zložené číslo. Ak n je zložené číslo, potom existujú celé čísla a,b také, že platí ab=n a zároveň 1\lt a,b\lt n. Nech a je z dvojice a,b to menšie číslo (resp. menšie alebo rovné ak platí a=b). Platí tak 1\lt a\leq b \lt n. Keďže sme v celých číslach, 1\lt a je to isté ako 2 \leq a. Potom dostávame odhad 2b \leq ab=n, odkiaľ po predelní číslom 2 máme b \leq \frac{n}{2}.
Všimnime si navyše, že pre n\geq 10 platí , že \frac{n}{2} \geq 5, a teda pripočítaním \frac{n}{2} k obom stranám platí aj n\geq \frac{n}{2}+5, takže odčitaním 5 dostávame aj \frac{n}{2}\leq n-5. Dokopy tak dostávame, že pre zložené n\geq 10 platí, že existujú celé a,b také, že ab=n a zároveň
2\leq a\leq b\leq \frac{n}{2} \leq n-5\lt n-4.
Vidíme tak, že ak tieto a,b sú rôzne (teda platí a\lt b), tak potom také n vyhovuje, keďže obe z čísel a,b sa nachádzajú niekde v množine \{1, \ 2, \cdots, n-4\}, a teda súčin prvkov tejto množiny bude deliteľný ab, čiže n=ab\mid (n-4)!.
Čo však v prípade, že platí a=b, teda, že n=a^2? Potom cheme ukázať, že a^2 \mid (a^2-4)!. Na to nám však stačí ukázať, že 2a\leq a^2 - 4. Potom by totiž platilo, že čísla a aj 2a sa nachádzajú v množine \{ 1, \ 2, \cdots, a^2-4 \}, a teda súčin prvkov tejto množiny by skutočne bol násobkom a^2. Táto nerovnosť vskutku platí, keďže n=a^2\geq 10 \implies a\geq\sqrt{10} \implies a\geq 4, a pre a\geq 4 platí
a^2 - 2a+ 1=(a-1)^2 \geq 9 ,
odkiaľ dostávame po úprave
a^2-4\gt a^2-8\geq2a.
Tým sme ukázali potrebnú nerovnosť, a teda sme s riešením hotoví.
Odpoveď: Vyhovujú všetky zložené čísla n\geq 10 a číslo n=8.
Bodovanie
Za "manuálne" vyksúšanie (niekoľkých) malých hodôt n sme udeľovali 1 bod. Ďalej, za vyriešenie prípadu kedy n je prvočíslom sme udeľovali 2 body. Za prípad kedy n=a\cdot b je zložené tak bolo udelovaných celkovo až 7 bodov. Z toho 4 za prípad kedy a\neq b, a 3 za prípad a=b.
Komentár
Pri úlohách kde chceme ukázať, že nejaká vlastnosť platí pre všetky čísla n (alebo skupinu čísel), nestačí ukázať, že daná vlastnosť platí pre prvých x čísel, a teda bude platiť už navždy. Treba nájsť nejaký argument pre všoebecné n, a neopierať sa iba o konkrétne hodnoty n.
Niektorí uvažovali pri prípade kedy n je zložené prvočíselný rozklad čísla n, avšak toto bola zbytočná komplikácia, a riešenie sa potom zamotalo. Pre túto úlohu plne stačilo uvažovať rozklad čísla n iba na dva činitele.
10. príklad
Označme si vrcholy trojuholníku A, B a C, ako na obrázku:
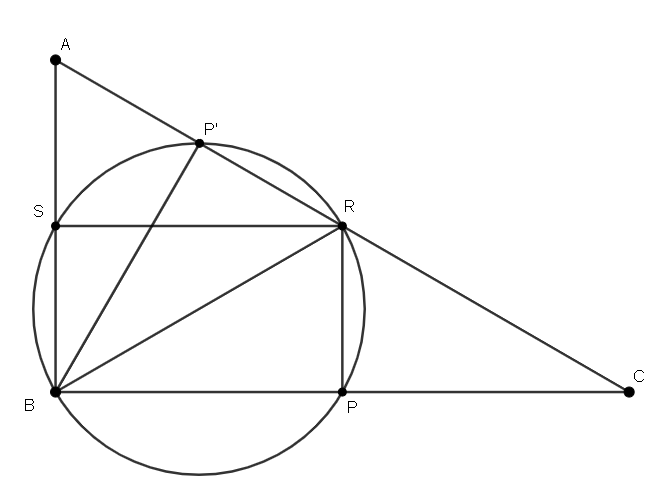
Vyznačili sme aj možného kandidáta na bod P - priesečník opísanej kružnice s priamkou AC, iný ako R. Označme ho P'. V tomto dôkaze sa pokúsime ukázať, že spojnica BP je kolmá na AC - teda je to výška, a P', ležiaci na opísanej kružnici SRQ, je naozaj pätou výšky P.
Poďme to teda ukázať! Vieme, že SR je stredná priečka trojuholníka ABC. Teda bude rovnobežná s jeho stranou, konkrétne BC. Keďže AB je kolmá na BC (lebo sme v pravouhlom trojuholníku), bude SR kolmá na AB.
Rovnako PR je stredná priečka rovnobežná s AB, teda bude kolmá na BC.
To znamená, že v štvoruholníku BPRS sú tri uhly pravé, teda je to obdĺžnik. Obdĺžnik má vždy opísanú kružnicu, a teda toto bude kružnica prechádzajúca P, R a S. Zároveň vieme, že v obdĺžniku leží stred opísanej kružnice v strede uhlopriečky, teda úsečka BR je priemerom tejto kružnice.
Keď vieme, že BR je priemerom kružnice, na ktorej leží P', tak Tálesova veta nám hovorí, že uhol BP'R bude pravý. Teda BP' je kolmá na P'R. Ale P'R je súčasťou AC, teda BP' bude výška na AC. Takže P' bude jej päta. To znamená, že naozaj, P' je P, a teda P leží na kružnici opísanej QRS. Čo bolo treba dokázať.