Vzorové riešenia 3. kola

Poďme sa zamyslieť nad tým, aké počty hráškov tam vlastne mohli byť. Vieme, že je z každej farby aspoň jeden. Čo ak by z nejakej farby boli dva?

Keby boli dva hnedé, tak potom keď si vyberieme trojicu, môže sa stať, že to budú tie dva hnedé a zelený. Takže by neplatilo to, čo povedal Benedikt. Toto platí aj v prípade, že by tých hnedých bolo ešte viac. Hnedých teda nemôže byť viac, teda je len jeden hnedý.

Niečo podobné vieme povedať aj o tých ostatných farbách. Keby boli aspoň dva žlté, môžeme si vybrať tie dva žlté a ešte zelený, čím by sme nedostali žiadny hnedý, teda by neplatilo, čo povedal Augustín. Teda aj žltý môže byť najviac jeden. No a keby boli dva zelené, tak si môžeme vybrať tie a žltý, a rovnako by nám chýbal hnedý. Takže aj zelený hrášok môže byť najviac jeden.

Zistili sme teda, že z každej farby máme iba jeden hrášok. Takže keď si vyberieme tri, tak sú to vždy tieto tri, a teda máme z každej farby aspoň jeden. Mendel mal teda pravdu.

Prvé čo si vieme všimnúť, je že ak má ľubovoľný z Marstonových kolegov 2​ susedov, tak je práve jedno z nasledujúcich tvrdení pravdivé:

• obaja jeho susedia sú klamári
  
• obaja jeho susedia sú pravdovravní
• práve jeden jeho sused je klamár a práve jeden jeho sused je pravdovravný

To je jasné :), ak obaja susedia Marstonovho kolegu sú pravdovravní, tak určite ani jeden z nich nie je klamár nie to ešte dvaja. Bezohľadu na to, ktorá z týchto situácií nastane Marston sa svojho kolegu môže opýtať všetky 3 otázky a ak je kolega pravdovravný, tak raz odpovie áno a dvakrát nie. Ak je klamár, tak dvakrát odpovie nie a raz áno. Vďaka tomu Marston dokáže o každom kolegovi, ktorý nie je krajný povedať, či je klamár, alebo pravdovravný.

Tak čo spravíme s krajnými kolegami?

Musíme rozlíšiť dva prípady:

Pokiaľ máme aspoň 3 ľudí na ktorých Marston skúšal svoj detektor lži, tak to je jednoduché. Spýtame sa krajného kolegu, či je jeho sused pravdovravný, a uvidíme či hovorí pravdu. Ak odpovie áno a jeho sused je skutočne pravdovravný, čo už vieme z prvej časti, alebo odpovie nie a jeho sused je skutočne klamár tak aj náš krajný kolega je pravdovravný. V opačnom prípade je klamár. Vďaka tomu ak máme aspoň 3 ľudí na ktorých testujeme detektor lži, tak vieme zistiť, kto je pravdovravný a kto je klamár.

Nakoniec ak máme ľudí iba 2, tak sme sa dostali do zložitej situácie. Nikto nemá dvoch susedov a teda nevieme o ňom priamo zistiť, či je pravdovravný, alebo klamár. Problém je, že ak sú obaja pravdovravní, aj ak sú obaja klamári, tak nám dávajú rovnaké odpovede. Rozlíšme kolegiňu Annu​ a kolegu Boba.

Najprv predpokladajme, že sú obaja klamári a postupne sa ich pýtajme otázky:

• Marston: "Anna, je tvoj sused Bob klamár?", Anna: "Nie." (zaklamala).
• ​Marston: "Anna, je tvoj sused Bob pravdovravný?", Anna: "Áno." (zaklamala).
• Marston: "Bob, je tvoja susedka Anna klamárka?", Bob: "Nie." (zaklamal).
• ​​Marston: "Bob, je tvoja susedka Anna pravdovravná?", Bob: "Áno." (zaklamal).

Teraz predpokladajme, že sú obaja pravdovravní a postupne sa ich pýtajme otázky:

• Marston: "Anna, je tvoj sused Bob klamár?", Anna: "Nie." (hovorí pravdu).
• ​Marston: "Anna, je tvoj sused Bob pravdovravný?", Anna: "Áno." (​hovorí pravdu).
• Marston: "Bob, je tvoja susedka Anna klamárka?", Bob: "Nie." (hovorí pravdu).
• Marston: "Bob, je tvoja susedka Anna pravdovravná?", Bob: "Áno." (hovorí pravdu).
  

Tým sme vyčerpali všetky možné otázky,  ktoré sa Anny a Boba môžeme spýtať, avšak nepodarilo sa nám zistiť, či sú obaja pravdovravní, alebo klamári, v oboch prípadoch odpovedajú rovnako.

Odpoveď: Pokiaľ Marton testuje detektor lži aspoň na 3 kolegoch, tak vie zistiť kto je klamár a kto je pravdovravný. Pokiaľ ho testuje iba na 2, tak nie.

Úloha po nás chce aby sme zistili, či sa dá vytvoriť náhrdelník pozostávajúci iba z perličiek (P​) alebo iba z korálok (K​). Chceme vlastne nájsť postupnosť náhrdelníkov takú, že prvý náhrdelník bude tvorený 4\,K a 5\,P, posledný bude mať iba K​ alebo iba P a vždy ten ďalší náhrdelník vznikne z posledného vyrobeného aplikáciou pravidiel zo zadania.

Máme dve možnosti ako môže výsledný náhrdelník vyzerať. Poďme sa pozrieť, z ktorých náhrdelníkov vieme tento finálny stav dosiahnuť:​

• ​stav iba P​:​
  Aby sme dostali samé P, tak musí každá dvojica susedných ozdôb byť rôzna. Skúsme nejaký takýto náhrdelník zostrojiť. Začneme P, potom musíme dať KPKPKPK. Ale poslednú ozdobu už navliecť nemôžeme, ak by sme navliekli P, tak budú 2\,P vedľa seba (prvá a posledná ozdoba susedia), ak by sme navliekli K, tak budú zase 2\,K po sebe. Takže takúto pozíciu nevieme dosiahnuť hneď na začiatku. Čo sa stane ak využijeme pravidlá zo zadania? Majme náhrdelník PKPKPKPKP \rightarrow PPPPPPPPK \rightarrow KKKKKKKPP \rightarrow \dots \rightarrow PKKKKKKKP. Tu si môžeme všimnúť, že tretí a posledný náhrdelník sú ten istý, len inak zrotovaný, takže ak by sme pokračovali ďalej, tak by sme sa iba zacyklili a vyrábali stále tie isté náhrdelníky. To znamená, že náhrdelník, ktorý je tvorený iba P nevieme vytvoriť (inak by sme ho už našli pred dokončením cyklu)
  
  
• ​stav iba K​:
  ​Aby sme dostali samé K, musí každá dvojica ozdôb v predchádzajúcom náhrdelníku byť rovnaká. To znamená, že predchádzajúci náhrdelník už mal iba samé K alebo samé P. Ak by mal iba K, tak sme zase "na konci", takže by už hneď na začiatku muselo byť 9\,K, čo nie je. Čiže by tam museli byť samé P. Ako sme ukázali vyššie, tak náhrdelník iba z P sa vytvoriť nedá, takže ani tento sa vytvoriť nedá.​
  

Odpoveď:

Neandrtálci nevedia vytvoriť náhrdelník, na ktorom budú iba ozdoby jedného druhu.

​​Cifry, ktoré si Newton vybral nazveme a,b,c​. Možnosti pre trojciferné čísla vytvorené z cifier a,b,c sú tieto:  abc, acb, bca, bac, cab, cba.​​
Ďalej budeme pracovať s desiatkovým rozkladom týchto čísel. Napríklad číslo abc​ bude mať desiatkový rozklad 100 \cdot a+10 \cdot b+1 \cdot c​. Teraz si zoberme súčet všetkých týchto čísel:

​abc+acb+bca+bac+cab+cba = 200a + 20a + 2a + 200b + 20b + 2b + 200c + 20c + 2c​​
Vidíme, že a​ je na mieste stoviek dvakrát, na mieste desiatok dvakrát a aj na mieste jednotiek dvakrát. To isté platí aj pre b​ aj pre c​.

To znamená, že po úprave dostaneme:

​abc+acb+bca+bac+cab+cba = 222(a+b+c)​​

Zo zadania vieme, že 3348​ je súčet piatich z týchto šiestich čísel a teda platí, že
222(a+b+c) = 3348 + abc​. (Náhodne sme si vybrali abc​, pretože nakoľko sa cifry rovnako často v tých šiestich číslach opakujú, je jedno ktoré z čísel vyberieme.)

Pozrime sa teraz na krajné možnosti čísla abc.

​Najviac, čomu sa môže abc rovnať je 987​, pokiaľ by sme použili tri najväčšie cifry. Pokiaľ si to dosadíme za abc​, dostaneme rovnicu:
​222(a+b+c) = 4335

Najmenej, čomu sa môže abc​ rovnať je číslo 123​, pokiaľ by sme použili tri najmenšie cifry. Pokiaľ si to dosadíme za abc​, dostaneme rovnicu:
​222(a+b+c) = 3471

​​Z tohto nám vyplýva, že ideme hľadať také násobky 222​, ktoré sú menšie ako 4335​ ale väčšie ako 3471​. To sú nasledovné:

​222 \cdot 16 = 3552
​222 \cdot 17 = 3774
222 \cdot 18 = 3996
222 \cdot 19 = 4218​​​​

​​Nakoľko tu sme našli možnosti pre súčty všetkých šiestich čísel, ale v zadaní sa nás pýtajú na posledné číslo, ktoré Newton nezarátal do súčtu, musíme od týchto súčtov všetkých šiestich čísel odrátať 3348​, čo je súčet piatich z nich.

 ​222 \cdot 16 - 3348 = 204​​
​222 \cdot 17 - 3348 = 426​​
​222 \cdot 18 - 3348 = 648​​
​222 \cdot 19 - 3348 = 870

Teraz zistíme, ktoré z týchto možností by naozaj mohlo byť to posledné číslo:

204​ ani 870​ to byť nemôžu, keďže vieme, že Newton si vybral nenulové cifry.
462​ to byť nemôže, pretože jeho ciferný súčet (a+b+c)​ je 12​ no malo by byť 17​.
648​ to môže byť, pretože jeho ciferný súčet je 18​, čo sedí.

Odpoveď: Dokázali sme, že jediné číslo, ktoré Newton nezarátal do súčtu je 648​.

Označme si hodnoty v štvorcoch x,y a z ako na obrázku. Potom súčet v 3. riadku bude x+y+z.

​

Na uhlopriečke z ľavého horného do pravého dolného rohu bude však súčet x+y+z+dva biele štvorce. To znamená, že súčet v tých dvoch štvorcoch musí byť 0 a keďže všetky čísla v štvorcoch musia byť nezáporné, tak v dvoch bielych štvorcoch musia byť nuly.

Rovnakú úvahu spravme s 3. stĺpcom a druhou uhlopriečkou. Z toho vyplýva, že vo zvyšných dvoch bielych štvorcoch musia byť tiež nuly.

V každom riadku, stĺpci a na každej uhlopriečke musí byť teraz súčet x+y+z, lebo tento súčet už máme v 3. riadku.

V 1. stĺpci máme zatiaľ y a červený štvorec a chceme, aby bol súčet x+y+z, teda v červenom štvorci musí byť x+y+z-y=x+z

V 5. stĺpci máme zas z a červený štvorec, teda v červenom štvorci bude x+y++z-z=x+y

V 2. riadku máme teraz y,x+y a k tomu modrý štvorec. teda v modrom štvorci musí byť x+y+z-y-(x+y)=z-y

V 4. riadku máme zas z, x+z a ešte modrý štvorec, teda ten musí mať hodnotu x+y+z-z-(x+z)=y-z

Teraz máme štvorec s hodnotou z-y aj štvorec s hodnotou y-z. Ak by bolo ​z\gt y, potom by bolo y-z  záporné a ak y\gt z, tak zas z-y bude záporné. No všetky čísla vo štvorcoch musia byť nezáporné, teda musí platiť y=z

Potom z-y aj y-z sú rovné 0, teda súčet v treťom stĺpci je 0+x+0=x, teda všade musí byť súčet x.

V treťom riadku je súčet x+y+z a chceme, aby aj toto bolo x. Teda x+y+z=x , z toho y+z=0 a keďže sú nezáporné, tak musia byť obe 0.

Teraz teda vieme, že v každom bielom a v každom modrom štvorci je 0.  Ostali nám teda už len červené štvorce a žltý štvorec. Ak skontrolujeme obe uhlopriečky, všetky riadky a všetky stĺpce, zistíme, že v každom je práve jeden červený, alebo žltý štvorec. Teda hodnota každého riadku, stĺpca a uhlopriečky je práve jeden žltý, alebo jeden červený štvorec. Keďže sú súčty rovnaké, tak aj čísla v červených a žltom štvorci musia byť rovnaké a tým, že je v každom riadku, stĺpci a na každej uhlopriečke práve jeden takýto štvorec, tak to číslo, ktoré dáme do červených a žltého štvorca môže byť ľubovoľné.

​​Odpoveď: všetky možnosti vyplnenia štvorca sú také, kde v červených štvorcoch a žltom štvorci je všade rovnaké číslo a v ostatných štvorcoch sú nuly.

​

Môžeme si všimnúť, že ak na jednej kocke sa nachádza viac stien s rovnakým počtom bodiek, tak jednu z nich si môžeme odmyslieť a stále získať všetky súčty ako s ňou. To znamená, že ak chceme zmyť čo najviac bodiek a máme nejaké dve steny na jednej kocke s rovnakým počtom bodiek, tak jednu z jednej z nich môžeme ubrať všetky bodky až na jednu.

Keďže na každej stene musí byť aspoň jedna bodka, tak jediná možnosť ako dosiahnuť súčet 2​ je 1+1​. Takže na oboch kockách je aspoň jedna strana, ktorá má na sebe práve jednu bodku. Keďže na každej stene je najviac 6​ bodiek, tak jediná možnosť ako dosiahnuť súčet 12​ je 6+6​. Takže na oboch kockách je aspoň jedna strana, na ktorej sa nachádza práve šesť bodiek.

Dosiahnuť súčet 3​ sa dá len ako 1+2​ a súčet 11​ len ako 5+6​, takže sa na niektorej z kociek nachádza strana s dvomi bodkami a na niektorej z kociek sa nachádza strana s piatimi bodkami.

Súčet 10 sa dá dosiahnuť len ako 4+6 alebo 5+5, takže bude musieť existovať stena so štyrmi bodkami, alebo ďalšia s piatimi bodkami. Súčet 4 sa dá dosiahnuť len ako 1+3 alebo 2+2. 

Zistili sme, že nutne musia existovať steny s týmito počtami bodiek na sebe: 1, 1, 2, 5, 6, 6 a potom niektorá z 2, 3 a niektorá z 4, 5. Takže minimum bodiek (teda maximum zmytých bodiek), ktoré potrebujeme je 1+1+2+5+6+6+2+4+4\cdot1 = 31, kde sme doplnili na zvyšné steny najmenej bodiek, teda jednu bodku. 

Keď zoberieme kocku s číslami 1, 1, 1, 2, 5, 6 a kocku s číslami 1, 1, 1, 2, 4, 6, tak vieme vyskadať všetky súčty od 2 po 12. Pri takýchto kockách sme zmyli 11 bodiek, čo je maximum.​

Odpoveď: Najviac sa mohlo zmyť 11 bodiek.

Túto úlohu vieme vypočítať zistením obsahu všetkých častí lichobežníka a následným sčítaním týchto čatí (viď obrázok).

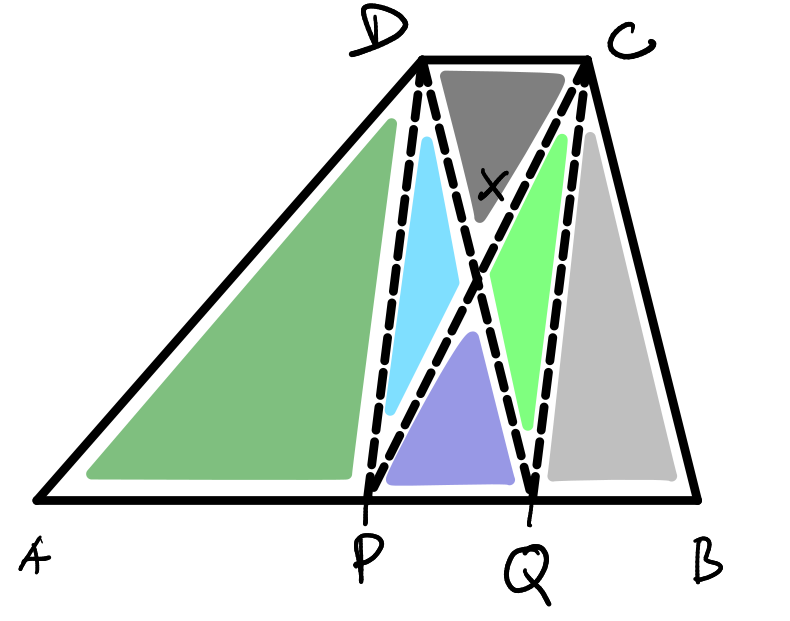
Zatiaľ však nemáme potrebné informácie na to, aby sme také vedeli spraviť, poďme teda poskúšať, čo všetko vieme z informácií v zadaní.

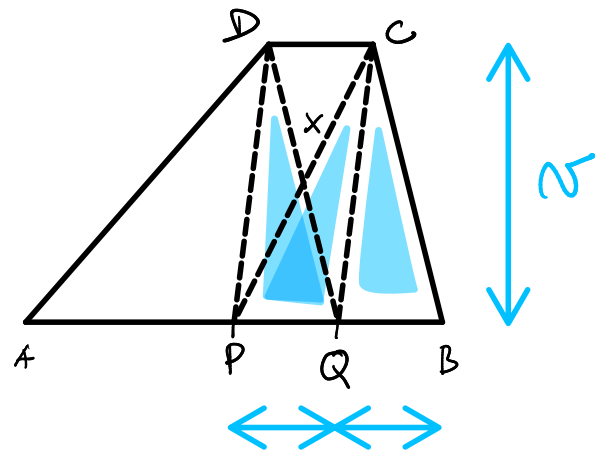
Trojuholník PQC má rovnaký obsah ako trojuholník QBC keďže majú rovnako dlhú stranu, lebo |PQ| = |QB| = 1, a výška na túto stranu je prakticky pre oba trojuholníky zhodná s výškou lichobežníka. To isté platí aj pre trojuholník PQD. Takže S_{QBC} = S_{PQC} = S_{PQD} = 2. 

Taktiež si vieme vypočítať výšku lichobežníka v z obsahu jedného z týchto trojuholníkov napríklad PQD:

​S_{PQD} = \frac{|PQ| \cdot v}{2}

2 = \frac{1\cdot v}{2}

v=4​​

Trojuholník APD​ má dvakrát väčšiu stranu ako trojuholník QBC ale rovnakú výšku, keďže |AP| = 2 a |QB| = 1, čo znamená, že má dvakrát väčší obsah: S_{APD} = 2 \cdot S_{QBC} = 4.

Vieme, že S_{DPX} = 1​ a S_{PQD} = 2. Keďže S_{PQD} = S_{DPX}+S_{PQX}​, tak z toho vyplýva, že S_{PQX}= 1 a analogicky aj S_{QCX} = 1​. Zakreslime si to do obrázka.

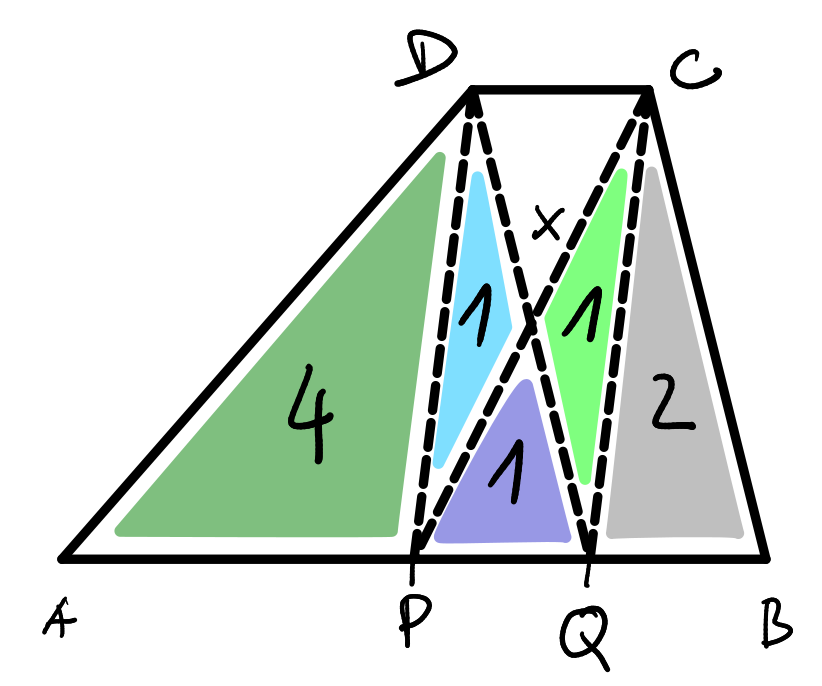
Zostala nám posledná časť, a to trojuholník DCX​. Nevieme o ňom ani výšku, ani stranu.

Poďme sa teda nejako zamyslieť, ako vieme vypočítať obsah trojuholníka DCX​

Obsah trojuholníka DCX vypočítame nasledovne S_{DCX} = \frac{c \cdot v_c}{2}. Ak vieme výšku celého lichobežníka, vedeli by sme od nej odčítať výšku trojuholníka PQX  a potom by sme dostali v_c (viď obrázok).

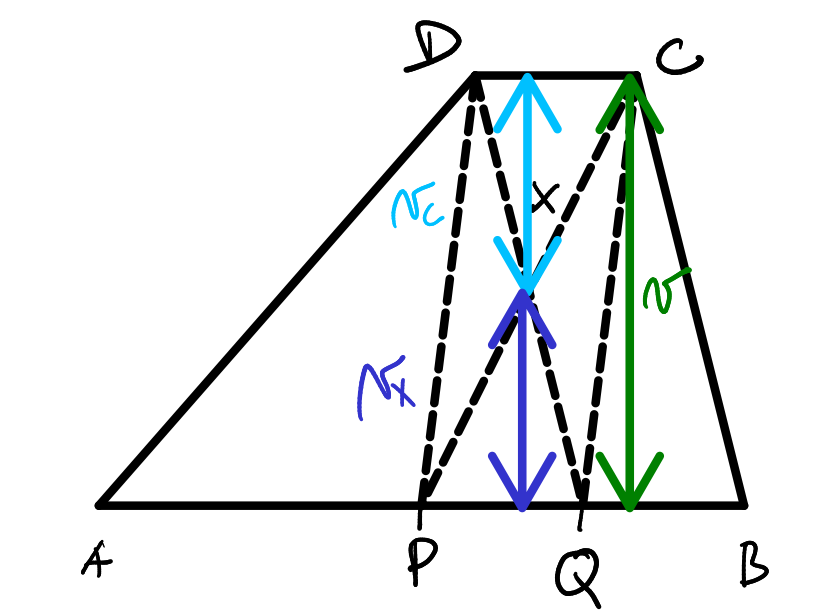
Výšku trojuholníka PQX​ vypočítame vďaka tomu, že vieme obsah a stranu tohto trojuholníka:

​S_{PQX} = \frac{|PQ| \cdot v_x}{2}​​

​1 = \frac{1 \cdot v_x}{2}​​

​2 = v_x​​

A teda výšku v_c​ nášho trojuholníka DCX vypočítame odčítaním od výšky lichobežníka v=4​, ktorú sme si vypočítali vyššie:

v_c = v - v_x

v_c = 4-2 = 2

Vidíme, že trojuholníky DCX a PQX majú zhodné výšky.

Čo je ďalej na týchto trojuholníkoch zaujímavé, sú ich uhly.

Vrcholové uhly budú zhodné:

|\measuredangle PXQ| = |\measuredangle DXC|​ 

A takisto aj striedavé uhly budú zhodné:

​|\measuredangle QPX| = |\measuredangle DCX|

|\measuredangle PQX| = |\measuredangle CDX|

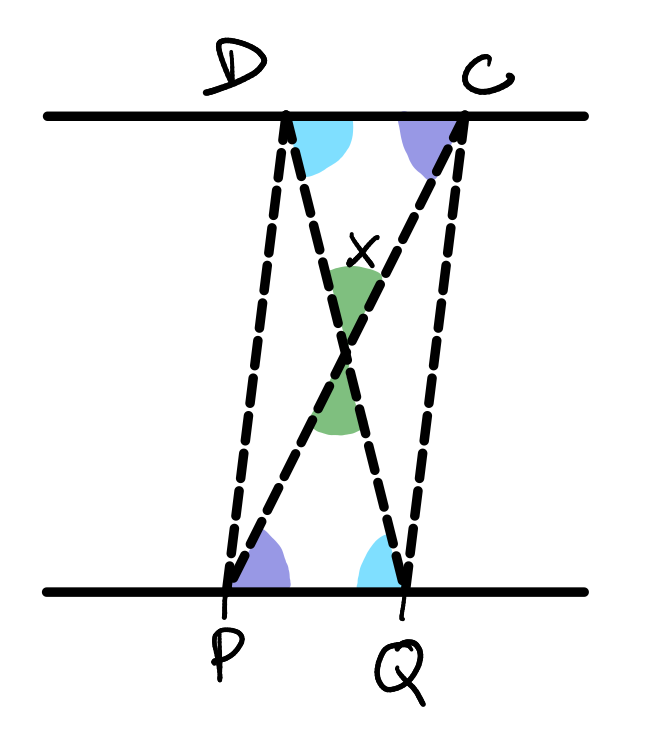
Z toho vyplýva, že trojuholníky DCX a PQX sú podobné, no zároveň majú rovnakú výšku, takže sú zhodné. To znamená, že majú rovnaký obsah a dĺžky strán:
​S_{PQX} = S_{DCX} = 1

​​Teraz už vieme aj obsahy všetkých trojuholníkov v lichobežníku a ich sčítaním vieme vypočítať obsah.

​S = 4+1+1+1+1+2 = 10​​

Odpoveď: Obsah celého lichobežníka ABCD je teda 10.

Podúloha a:

Pri tejto podúlohe vidíme, že nám netreba nájsť len 1 príklad umiestnenia 2 žiaroviek, ktoré neosvetlia celú miestnosť. Z toho nemôžeme usúdiť, že akékoľvek iné umiestnenie taktiež neosvetlí miestnosť. Vieme ale zadanie zjednodušiť tak, aby sa dalo dokázať príkladom.

Zamyslíme sa nad týmto tvrdením: "existuje trojica bodov taká, že ich nevieme osvetliť 2 žiarovkami". Toto tvrdenie je o dosť jednoduchšie dokázať, stačí len dobre zvoliť 3 body a ukázať prečo ich nevieme osvetliť 2 žiarovkami.

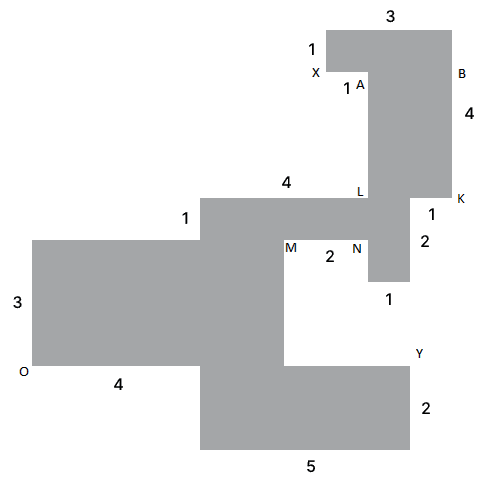
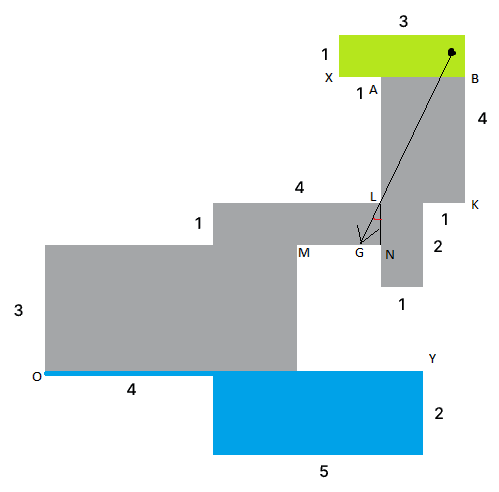
Označme si v miestnosti všetky dôležité body (viď obrázok). Pozrime sa na body X a Y. Teraz sa môžeme zamyslieť nad tým, z kadiaľ ich vieme osvedliť. Všimnime si, že bod Y je v rohu, takže všetky lúče, ktoré doňho môžu ísť, smerujú doprava, hore alebo niečo medzi (viď obrázok). Takisto, bod X je v rohu a všetky lúče smerujú doľava, dole, alebo niečo medzi (viď obrázok). Modrou vyfarbíme všetky miesta, kde vieme dať žiarovku tak, aby bol bod Y osvetlený a zelenou všetky miesta, kde vieme dať žiarovku tak, aby bol bod X osvetlený. Všimnime si, že na modro je vyfarbená celá úsečka OY, to je kvôli tomu, že lúč môže ísť po hrane.

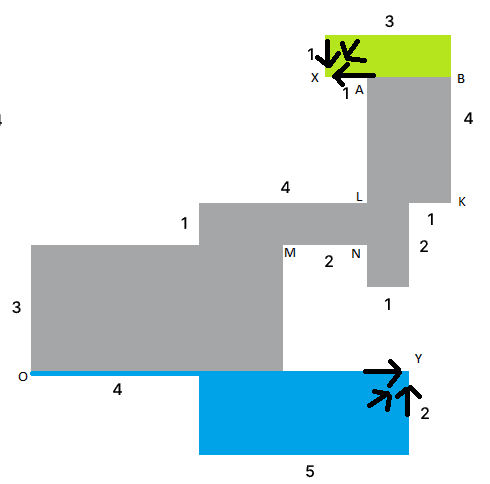
Teraz skúsme nájsť bod, ktorý nevieme osvetliť ani z modrej, ani zo zelenej zóny. Pozrime sa na úsečkuMN, pretože tá vyzerá ako miesto, kde sa môže takýto bod nachádzať. Je celkom zrejmé, že z modrej zóny vieme osvetliť len bod M, ak by sme chceli osvetliť ostatné body, museli by sme prejsť cez stenu.

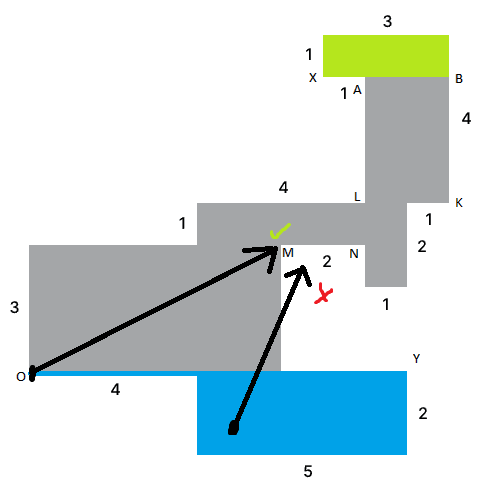
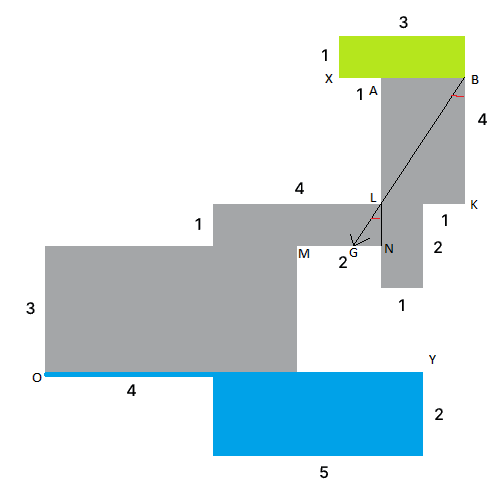
Teraz sa pozrieme, ktoré body z MN vieme osvetliť zo zelenej zóny. Predstavme si, že máme žiarovku niekde v zelenej zóne tak, aby z nej išiel lúč cez bod L a dopadne niekde na priamke MN (tento bod nazvyme G) ako na obrázku. Môžeme potom usúdiť, že všetky body na úsečke GN budú osvetlené. Chceme aby mala GN čo najväčšiu dĺžku, to znamená že chceme aby uhol medzi lúčom a LN bol čo najväčší (viď obrázok). Je celkom zrejmé, že najväčší uhol dostaneme tak, že žiarovku umiestnime do bodu B.

Dlžku GN zistíme pomocou podobnosti trojuholníkov. Všimnime si, že trojuhoľníky GNL a LKB sú podobné, tým že oba sú pravouhlé a prislúchajúce uhly (GLN a LBK) majú rovnakú veľkosť (GLN a LBK sú súhlasné uhly). To znamená, že pomery prislúchajúcich strán budú rovnake. Strana NL má dĺžku 1 a strana KB má dĺžku 3. Z tohto vidíme, že strana LK bude mať 3-krát väčšiu veľkosť ako strana GN. LK má veľkosť 2, to znamená že GN má veľkosť \frac{2}{3}.

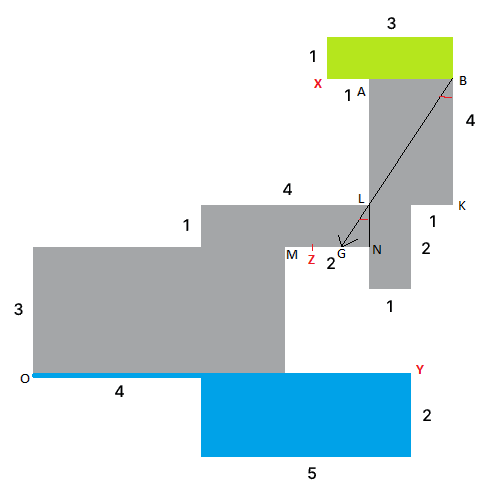
Teraz si všimnime, že sa bod G určite nachádza v úsečke MN, tým že null a to znamená, že medzi bodmi M a G nebude ani jeden osvetlený bod. To znamená, že existuje bod, ktorý nevieme osvetliť z modrej, ani zo zelenej zóny. A to znamená, že existuju 3 body také, že ich nevieme osvetliť iba 2 žiarovkami (napríklad body X,Y,Z), tým pádom sa celá miestnosť nedá osvetliť 2 žiarovkami

Podúloha b. 

Táto podúloha je výrazne ľahšia, stačí nám len nájsť umiestnenie 3 žiaroviek a ukázať, že osvetlí celú miestnosť.

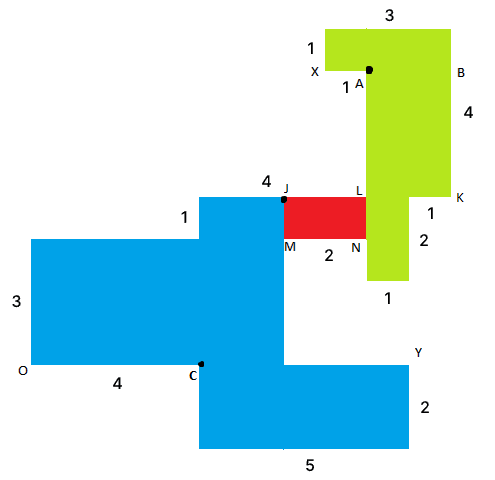
Zoberme si napríklad body C a A a umiestnime do nich žiarovku. Žiarovka v bode C určite rozosvieti na modro vyfarbenú zónu (dostane sa aj k bodu Y, pretože lúč môže ísť po stene). V skutočnosti táto žiarovka toho osvetlí aj nejaku časť z obdĺžnika JLNM, ale tieto časti osvetlí tretia žiarovka, takže sa nimi nemusíme zaoberať. A žiarovka v bode A určite osvetlí všetky zelené zóny. Zostáva nám už len spomínaný obdĺžnik JLNM, do ktorého môžeme kamkoľvek umiestniť žiarovku, napr. do bodu J (časti osvetlené z J som vyfarbil na červeno). A tým pádom máme hotovo! Našli sme vhodné umiestnenie žiaroviek (body C,A,J) a ukázali sme, že skutočne osvetlia celú miestnosť.

Budeme dokazovať toto tvrdenie sporom. Pokúsime sa teda kartičky rozdeliť tak, aby ani Pierre ani Mária postupnosť nemali, a zistíme, že sa to nedá.

Keďže rozdeľujeme všetky kartičky, tak každý bude mať na konci 5 kartičiek. Preto ak ukážeme, že jeden z nich nemôže mať nejakú kartičku, určite ju musí mať ten druhý.

Môžeme si všimnúť, že ak by jeden hráč mal 3​ a 5​, tak by vytvoril postupnosť s: (1, 3, 5​), aj s 4​ (3, 4, 5​) aj so 7​ (3, 5, 7​), teda druhý hráč musí mať 1​, 4​ aj 7​. To ale nefunguje, lebo 1, 4, 7​ je tiež aritmetická postupnosť, a teda ak ju nechceme vytvoriť, žiaden hráč nemôže mať aj 3 aj 5.

To isté vieme povedať o dvojiciach 4​ a 6​, 5​ a 7, 6​ a 8:

• 4​ a 6 nemôžu byť s 2​, 5​ ani 8​, ktoré potom tvoria postupnosť u druhého hráča
• ​5​ a 7​ nemôžu byť s 3​, 6​ ani 9​, ktoré tvoria postupnosť
• 6 a 8 nemôžu byť s 4​, 7​ ani 10​, ​ktoré tvoria postupnosť

Teda dvojice 3​ a 5​, 4​ a 6​, 5​ a 7​ ani 6​ a 8​ nemôže mať jeden hráč. To znamená, že ten hráč, ktorý bude mať 5​ nebude mať 3​ ani 7 - bude ich musieť mať druhý hráč. Podobne ten čo bude mať 6​ nemôže mať 4​ ani 8​, a teda má obe druhý hráč.
Pozrime sa teraz na možnosti, ako môžu byť rozdelené dvojice 3​ a 7​, 4​ a 8​. Najprv na možnosť, kde má všetky tieto čísla jeden hráč, a neskôr na druhú možnosť kde 3, 7​ má jeden a 4​, 8​ má druhý.

Ak má jeden z nich  3, 4, 7, 8, tak nemôže mať:

• ​1​ (1, 4, 7​ je postupnosť) 
• ​2​ (2, 3, 4​ je postupnosť)
• ​5​ (3, 4, 5​ je postupnosť)
• ​6​ (6, 7, 8​ je postupnosť)
• ​9​ (7, 8, 9​ je postupnosť)
• ​10​ (4, 7, 10​ je postupnosť)

To boli ale všetky zvyšné kartičky, a teda nech má hocijakú štvrtú kartičku, vytvorí postupnosť.
Vieme preto, že jeden hráč musí mať 7, 3​ a druhý 8, 4​. Poďme to skúsiť.

Ten kto má 7, 3​ (nazveme ho prvý) nemôže mať 5​, lebo 3, 5, 7​ je postupnosť. Druhý teda musí mať 5​, a potom nemôže mať 6​, lebo už má 4, 8​ a 4, 5, 6​ by bola postupnosť. Teda prvý musí mať 6, preto  nemôže mať 9​, lebo by to vznikla postupnosť 3, 6, 9. Ak druhý musí mať 9, tak nemôže mať 10​, lebo 8, 9, 10​ je postupnosť. Prvý musí mať 10​, a preto nemôže mať 2​, lebo 2, 6 ,10​ je postupnosť. Ak ale druhý musí mať 2 dostane postupnosť 2, 5, 8​, a teda sa postupnosti nedá vyhnúť ani tu.

Odpoveď: Zistili sme, že vo všetkých možnostiach nám vznikne postupnosť, ktorú budeme vedieť vybrať z kartičiek jedného hráča.

V riešení budeme predpokladať, že ľavá misa je vždy ťažšia ako tá pravá, pričom v prípade, že to tak nie je, bude váha ukazovať záporné číslo. Táto úprava úlohu nemení.

Najprv si ukážeme, že keď ľubovoľne mince rozdelíme do ľavej misy, pravej misy a mimo váhu, tak vždy budeme vedieť určiť, v ktorej skupinke sa nachádza každá minca. Ukážeme to tak, že číslo, ktoré ukáže váha, unikátne určí polohu každej mince. Teda žiadne dve rôzne rozpoloženia mincí neukážu rovnaké číslo.

Ukážeme si to sporom, takže nech existujú dve rôzne rozpoloženia mincí také, že ukážu rovnaké číslo. Číslo na váhe je súčet mincí na ľavej strane mínus súčet mincí na pravej strane, takže dostaneme:

​\pm 3^{\alpha_1} \pm 3^{\alpha_2} \pm \dots \pm 3^{\alpha_n} = \pm 3^{\beta_1} \pm 3^{\beta_2} \pm \dots \pm 3^{\beta_m}​

Pričom kladné členy sú na ľavej mise, záporné členy na pravej mise a pre exponenty platí: \alpha_1 < \alpha_2 < \dots < \alpha_n a \beta_1 < \beta_2 < \dots < \beta_m. 

Ak \alpha_1 \neq \beta_1, tak vieme obe strany predeliť 3^{\min(\alpha_1,\beta_1)} . Potom na jednej strane bude číslo deliteľné 3 a na druhej nebude deliteľné 3 takže dostávame spor a tým pádom \alpha_1 = \beta_1. Ďalej keď sa pozrieme na znamienka pri 3^{\alpha_1} a 3^{\beta_1}, tak ak by boli rôzne, tak by sme dostali:

2(\pm 3^{\alpha_1}) =\pm 3^{\alpha_2} \pm \dots \pm 3^{\alpha_n} \pm 3^{\beta_2} \pm \dots \pm 3^{\beta_m}

Kde po predelení 3^{\alpha_1} dostaneme, že 2 je rovné číslu deliteľnému 3, čo je spor. Takže dostávame, že 3^{\alpha_1} = 3^{\beta_1} a že majú rovnaké znamienko, takže v oboch rozdeleniach je minca s váhou 3^{\alpha_1} na rovnakej mise. 

Mincu s váhou 3^{\alpha_1}​ teda môžeme odobrať z oboch rozpoložení mincí a získať tým nové 2 rôzne rozpoloženia mincí s rovnakým číslom na váhe. Tento proces však môžeme opakovať, čím zistíme, že n = m a \alpha_k = \beta_k pre ľubovoľné k. To však ale znamená, že ak dve rozpoloženia majú rovnaké číslo na váhe, tak to musia byť rovnaké rozpoloženia mincí.

Zistili sme, že nech ľubovoľne rozdelíme mince na váhy, vždy vieme povedať o každej minci to, že či sa nachádza na pravej mise, ľavej mise, alebo mimo váhy. 

Teraz sa pozrime, na koľko ťahov vieme nájsť mincu s váhou 1. Každým vážením sa nám mince rozdelia na 3 skupiny a my o každej minci vieme povedať v ktorej skupine sa nachádza. Ak využijeme n vážení, tak každá minca dostane nejakú postupnosť dĺžky n skladajúcu sa z troch typov skupín, v ktorých sa daná minca nachádzala v danom vážení. Ak chceme jednoznačne identifikovať mincu s váhou 1, tak musí mať svoju postupnosť rôznu od všetkých ostatných. Lebo ak dve rôzne váhy mincí majú rovnakú postupnosť, znamená to, vždy boli na tých istých váženiach a nevieme ich od seba odlíšiť. 

Dvomi váženiami môžeme získať najviac 3^2 = 9 rôznych postupností, teda po dvoch váženiach sa nám môže stať, že minca s váhou 1 bude mať rovnakú postupnosť ako minca s inou váhou a teda ich nebudeme vedieť rozlíšiť.

Teraz ukážeme, že na 3 váženia vieme nie len nájsť, ktorá minca má váhu 1, ale dokonca aj váhy všetkých mincí. Ako sme vyššie ukázali, nájsť váhu niektorej mince je ekvivalentné s priradením danej minci unikátnu postupnosť. Máme 27 mincí a existuje 3^3=27 postupností dĺžky 3 rozdelenia do 3 skupín. Takže každej minci vieme priradiť jednu postupnosť a podľa týchto postupností vieme v ktorom vážení máme dať ktoré mince do ktorej skupiny.​

Odpoveď: Mincu s váhou 1 vieme nájsť na najmenej 3 váženia (popis ako je popísaný vyššie), váhy všetkých mincí vieme tiež nájsť na najmenej 3 váženia (popis ako je tiež popísaný vyššie).