Vzorové riešenia 2. kola
1. príklad
V zadaní sa spomínajú čísla, ktoré nepoznáme, no vieme nejaké vlastnosti o ich cifrách. V takýchto prípadoch je veľmi praktické označiť si tieto cifry písmenkami. Prvý míľnik teda bude v tvare \overline{AB} , druhý v tvare \overline{BA} a tretí buď \overline{A0B} , alebo \overline{B0A} . Pričom \overline{AB} nereprezentuje súčin cifier A a B , ale jednotlivé cifry nejakého čísla, čo je dôvod, prečo nad tým píšeme čiarku.
Ďalšia vec, čo sa oplatí, je zamýšľať sa a postupne vymedzovať aké hodnoty môžu nadobúdať tieto cifry.
Akú maximálnu hodnotu teda môže nadobúdať tretí míľnik? Vieme, že hodnotu tretieho míľniku vypočítame ako súčet Fordovej rýchlosti a hodnoty na druhom míľniku. Čo vieme o týchto číslach? Keďže hodnota Fordovej rýchlosti je rozdielom hodnôt na druhom a prvom míľniku, ktoré sú oba dvojciferné, najviac dvojciferná bude aj táto rýchlosť. Keď od dvojciferného čísla odpočítavam dvojciferné, viem dostať najviac dvojciferné číslo. Takže tretí míľnik, je súčtom dvoch dvojciferných čísel - rýchlosti a druhého míľniku.
Keďže súčet dvoch najväčších dvojciferných čísel je najviac 99 + 99 = 198, vieme, že jedno z čísel A alebo B musí byť 1 . Keďže obe čísla sú dvojciferné, tak ani jedna z cifier nemôže byť 0 . Zároveň, keďže Ford ide stále konštantnou rýchlosťou a tretí míľnik je najväčší, tak vieme že druhý míľnik bude musieť byť tiež väčší ako prvý, takže aj jeho začiatočná cifra bude musieť byť väčšia, čo si vieme zapísať ako A \lt B. Tým pádom keďže ani jedna z cifier nie je 0 a jedna musí byť 1 , tak potom A musí byť 1.
Od tohto momentu vieme v našom riešení pokračovať viacerými spôsobmi:
Riešenie pomocou skúšania
Pri skúšaní sa vždy oplatí postupovať systematicky, preto skúšame v tabuľke, kde pre každé B najprv vypočítame hodnotu tretieho míľniku a potom ju porovnáme s hodnotou, ktorú by sme chceli aby tretí míľnik mal:
B | \overline{B1} + (\overline{B1} - \overline{1B}) = ? | \overline{A0B} |
2 | 21 + (21 - 12) = 30 | 102 |
3 | 31 + (31 - 13) = 49 | 103 |
4 | 41 + (41 - 14) = 68 | 104 |
5 | 51 + (51 - 15) = 87 | 105 |
6 | 61 + (61 - 16) = 106 | 106 |
7 | 71 + (71 - 17) = 125 | 107 |
Ďalej ako po 7 už vidíme, že skúšať netreba, keďže sa nám hodnoty na treťom míľniku budú len zväčšovať, a teda nebudú mať na mieste desiatok 0, ako by to malo podľa zadania byť.
Z tohto nám už vyšlo jasné riešenie, hodnoty míľnikov sú 16, 61 a 106. Rozdiel medzi nimi je vždy 45, čo je aj Fordova rýchlosť.
Riešenie pomocou rovníc
Fakt, že tretí míľnik je súčtom druhého a rýchlosti, si vieme zapísať nasledovne:
\overline{B1} + (\overline{B1} - \overline{1B}) = \overline{10B} ,
pričom ide o cifry a nie o súčin, ako naznačuje čiara nad číslami.
Takéto rovnice, kde neznáme znamenajú cifry a nie čísla, sú celkom nepraktické. My ale vieme, že pre číslo \overline{B1} platí, že \overline{B1} = 10 \cdot B + 1. Poďme si teda rovnicu zapísať takto upravenú a riešme:
\begin{aligned}10 \cdot B + 1 + 10 \cdot B + 1 - 10 - B &= 100 + B \\ 20 \cdot B - B + 2 - 8 &= 100 + B \\ 19 \cdot B - 8 &= 100 + B &/+ 8, - B \\ 18\cdot B &= 108 \\ B &= 6\end{aligned}
Z tohto nám opäť vyšlo B = 6 tak ako v riešení vyššie.
Odpoveď:
Ford išiel rýchlosťou 45 míľ za hodinu.
2. príklad
Najskôr sa pozrieme, aké jednotlivé počty bodov mohli Feynmanovi žiaci dosiahnúť. Máme 3 možnosti pre obidve otázky: správna odpoveď (3 body), nesprávna odpoveď (-1bod), neodpovedal (1 bod), a z toho vyplýva, že máme dokopy 3 \cdot 3 = 9 možností (Ku každému možnému obodovaniu prvej otázky vieme napárovať 3 možné obodovania druhej). Jednotlivé možnosti vyzerajú takto:
počet bodov z prvej otázky | počet bodov z druhej otázky | spolu |
|---|---|---|
3 | 3 | 6 |
3 | 1 | 4 |
3 | -1 | 2 |
1 | 3 | 4 |
1 | 1 | 2 |
1 | -1 | 0 |
-1 | 3 | 2 |
-1 | 1 | 0 |
-1 | -1 | -2 |
Z tabuľky vidíme, že je 5 rôznych počtov bodov z testu (6, 4, 2, 0, -2). Teraz sa môžeme zamyslieť, ako nájdeme najmenší počet študentov taký, kde určite majú aspoň 4 študenti rovnaký počet bodov. Čo tak sa na to pozrieť z opačnej strany? Ideme nájsť najväčší počet študentov kde sa taká skupinka nutne nemusí nachádzať. To znamená, že existuje aspoň 1 rozdelenie, kde všetky skupiny budú obsahovať menej ako 4 študentov.
Pozrime sa na prípad, že máme 15 študentov. Pri tomto počte ich vieme rozdeliť do piatich skupín po 3 (toto rozdelenie nazvyme "vyvážené"). Ako vidíme je to jediné rozdelenie 15 študentov, kde všetky skupinky maju pod 4 študentov. Iné rozdelenie dosiahneme tým, že vo vyváženom rozdelení premiestnime nejakých študentov z jednej skupinky do druhej. Toto nám ale zaručí vznik skupinky s aspoň 4 študentmi, keďže pridáme nejakých študentov do skupinky s 3 študentmi.
Pridaním 16. študenta máme zaručené, že aspoň jedna skupinka bude mať aspoň 4 študentov. Všetky rozdelenia 15 okrem vyváženeho už obsahujú skupinku aspoň 4 študentov. To znamená, že aj po pridaní študenta bude takáto skupinka existovať. Pri vyváženom rozdelení sa musí študent pridať do jednej skupinky 3 študentov, tým pádom by nám vznikla skupinka s 3 + 1 = 4 študentmi.
To znamená, že v triede muselo byť aspoň 16 študentov.
Komentár
Väčšina z vás síce došla k správnemu výsledku, ale nepodarilo sa vám úplne poriadne zdôvodniť, prečo to tak naozaj je. Väčšinou ste povedali, že keď je ich 15 tak, že v každej skupinke sú traja, tak keď pridáme ďalšieho, tak už v nejakej skupinke budú štyria. To je pravda, ale my chceme ukázať nielen to, ale že dokonca keď tých 16 ľudí rozdelíme úplne hocijako, tak stále budú niekde aspoň štyria. V tomto príklade to síce vyzerá pomerne zrejmé (preto sme za to nestrhávali body), ale aj tak je lepšie to poriadne vysvetliť, hlavne pri ťažších príkladoch, kde to už také zrejmé nie je.
3. príklad
Zo zadania poznáme tri podmienky:
Ak v dome býval človek, tak aj vo všetkých domoch, do ktorých z neho ide šípka, býval človek.
V každom riadku bývali aspoň 2 ľudia.
V každom stĺpci boli aspoň dva domy neobývané.
Najprv sa pozrieme na prvý stĺpec a na políčka E1 a D1. Vieme, že ak by bol dom na E1 obývaný, vďaka šípkam (a podmienke číslo 1) by boli obývané postupne aj D1, C1, B1, A2, A1. Tu nám ale nastáva spor s treťou podmienkou - v stĺpci by nebol žiadny dom, ktorý je neobývaný. Podobne to platí aj pri D1. Postupne, vďaka šípkam by boli obývané aj C1, B1, A2, A1. Tu nám znova nastáva spor s treťou podmienkou - v stĺpci by mohol byť iba jeden dom neobývaný (E1). Z tohto vyplýva, že domy E1 a D1 obývané byť nemôžu.

Teraz sa pozrieme na políčko B3. Ak by to bolo obývané, tak vďaka šípkam a prvej podmienke by boli obývané aj nasledujúce domy: A3, A4, A5, B5, C5, C4, B4, C3, C2, B2, A2, A1 a B1 - všetky v riadkoch A, B, C okrem C1. Toto by viedlo k tomu, že by v každom stĺpci okrem prvého domy v riadku D a E museli byť neobývané, aby bola splnená tretia podmienka. Tu nám nastáva spor s druhou podmienkou, ktorá hovorí o riadkoch - v riadku D a E by ostal iba jeden dom, ktorý by mohol byť obývaný (E1 a D1), no musia byť aspoň dva. Z toho nám vyplýva, že dom B3 obývaný byť nemôže.
Tento poznatok použijeme pri dome B3. Z políčka C2 ide šípka do B3, takže ten je tiež neobývaný. Rovnako to platí aj pri poličkach C3 a D3.
V každom riadku musia byť aspoň dva domy obývané, čo znamená, že v riadku D musia aspoň dva zo zvyšných 3 voľných domov byť obývané. Vidíme, že ak by bol obývaný dom D4, tak by bol vďaka šípke aj D5 a potom aj E5 a E4. Ak by bol až D5, tak aj tak by bol obývaný aj D4, pretože vďaka šípkam by boli obývané postupne E5, E4 a napokon aj D4.
Z toho nám vyplýva, že D5 a D4 sú isto obývané, nakoľko len D2 nestačí a tieto dva sú obývané vždy spolu.
Teraz sa pozrime na 5. stĺpec, kde zatiaľ vieme, že D5 aj E5 sú obývané. Tu vidíme, že ak by A5 bolo obývané, boli by postupne obývané aj B5 a C5 - čiže žiadny dom by nebol neobývaný. Ak by bolo obývané B5, tak by bolo zároveň aj C5 - čiže len jeden dom by mohol byť neobývaný. Z tohto nám vyplýva, že A5 aj B5 sú neobývané. Aplikujme tu teraz to pravidlo o neobývaných domoch. Z toho nám vyplynie, že tým pádom aj A4, A3, B4 a C4 sú neobývané.
V riadkoch A, B a C nám teraz ostávajú vždy už len dva domy, ktoré podľa druhej podmienky o riadkoch musia byť obývané - sú to A1, A2, B1, B2, C1, C5.
Ak je obývaný dom C1, podľa šípok a prvej podmienky vidíme, že aj D2 a E3 musia byť obývané.

No a aby platilo stĺpcové pravidlo o stĺpci 2, dom E2 musí byť neobývaný, pretože A2,B2 aj D2 sú obývané, len C2 nie je.

Týmto sme sa dopracovali k nasledujúcemu riešeniu:

Iné riešenie nie je, pretože ako sme si dokázali, ak by sa akýkoľvek neobývaný dom premenil na obývaný, jedna z podmienok by neplatila. Tak isto, ak by sa nejaký obývaný dom premenil na neobývaný, jedna z podmienok by neplatila.

4. príklad
Prvé pozorovanie, ktoré môžeme spraviť je, že keď prechádzame ľubovoľný útvar jedným ťahom, tak ak v danom vrchole nezačíname, ani nekončíme, vždy keď doň prídeme, musíme z neho odísť, takže prejdeme párny počet hrán z neho vychádzajúcich. Pri vrchole v ktorom začíname a pri vrchole v ktorom končíme prejdeme zas nepárny počet hrán, argument je podobný, len prvá, poprípade posledná cesta nemá dvojicu. Toto pozorovanie sa často veľmi hodí. V tomto príklade nám síce mohlo kúsok pomôcť, ale dá sa elegantne vyriešiť aj bez neho. Ešte dodajme, že keď danú myšlienku rozvinieme vieme zistiť, že prejdeme maximálne 9 z hrán nášho kvádrika.
Alain sa chcel dostať z jedného rohu budovy do protiľahlého. Nazvime ich A a F a označme ich oranžovou farbou. Ďalej môžeme predpokladať, že Alain začína v bode A (vieme kvádrik otočiť tak aby začínal v bode A). Všimnime si, že bod A je na spodnej a bod F je na hornej stene kvádra. Vždy keď Alain prelezie po modrej hrane, tak tým zmení či sa nachádza na spodnej alebo hornej stene kvádra. Takže Alain môže prejsť maximálne 3 z modrých hrán o dĺžke 60m, lebo ak prelezie párny počet hrán tak sa vráti späť na spodnú hranu.

Podobne bod A sa nachádza na prednej stene a bod F na zadnej, takže Alain môže preliezť maximálne 3 zo zelených hrán o dĺžke 40m. Nakoniec bod A sa nachádza na ľavej stene a bod F pravej stene. Červené steny o dĺžke 50 m, Alain tiež prelezie maximálne 3.
Dokopy dostávame, že väčšiu vzdialenosť, ako 3\cdot40 \text{m} + 3\cdot 50\text{m} + 3\cdot 60\text{m} = 450 \text{m} Alain určite neprelezie.
Na druhú stranu danú vzdialenosť vie preliezť napríklad ako na nasledujúcom obrázku. Číslo hovorí ako ktorý v poradí bude daný vrchol Alainom navštívený.
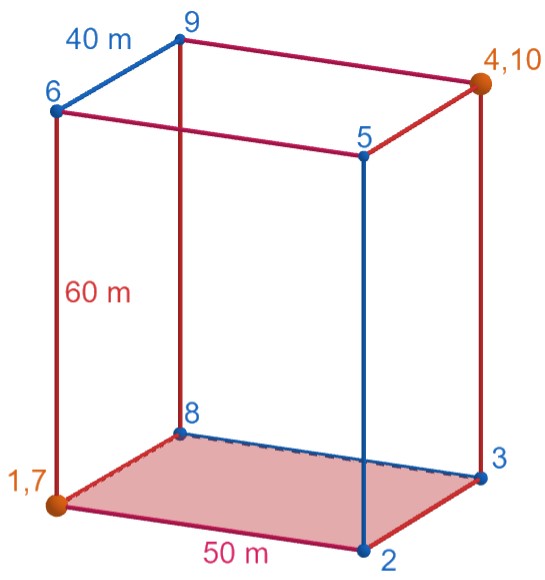
Odpoveď: Najdlhšia trasa, ktorú Alain môže prejsť mala 450\text{m}.
5. príklad
Nazvime si naše čísla tak, aby boli zoradené od najmenšieho: a \lt b \lt c \lt d \lt e.
Vieme, že najmenší súčet musel vzniknúť ako a+b. Druhý najmenší musel byť a+c lebo b+c, a+d a aj všetky súčty obsahujúce e vieme zmenšiť keď jeden zo sčítancov zmeníme za menší. Máme teda:
(1)\space\space\space a+b=0
(2)\space\space\space a+c=2
Podobne poznáme najväčší a druhý najväčší súčet.
(3)\space\space\space d+e=15
(4)\space\space\space c+e=13
Keď poznáme tieto súčty, vedeli by sme napríklad vypočítať hodnotu c, ak by sme poznali celkový súčet všetkých piatich čísel. Ale ten zistiť vieme! Všetkých 10 súčtov dáva dokopy 0+2+4+4+6+8+9+11+13+15=72, a každé číslo sa nachádza v štyroch súčtoch (z každým iným číslom raz). Teda 72=4\cdot a+4\cdot b+4\cdot c+4\cdot d+4\cdot e, po vydelení štyrmi a+b+c+d+e=18. Teraz môžeme odčítať rovnice (1) a (2). Teda a+b a d+e z jednej strany, a ich súčty 0 a 15 z druhej. Ostane nám c = 3.
Po dosadení tejto hodnoty do rovníc (2) a (4) dostávame:
(2)\space\space\space a+3=2\implies a=-1
(4)\space\space\space e+3=13\implies e=10
a môžeme ďalej dosádzať:
(1)\space\space\space -1+b=0\implies b=1
(3)\space\space\space d+10=15\implies d=5
Teraz už poznáme všetkých päť čísel, a vieme že žiadne iné by nemohli sedieť. Ostáva nám teda už len presvedčiť sa, že je to správne riešenie, a naozaj dostaneme zadané súčty:
a | b | c | d | e | |
+ | -1 | 1 | 3 | 5 | 10 |
-1 | 0 | 2 | 4 | 9 | |
1 | 4 | 6 | 11 | ||
3 | 8 | 13 | |||
5 | 15 | ||||
10 |
Odpoveď: Čísla na kartičkách boli -1, 1, 3, 5, 10
6. príklad
Začneme tým, že si všimneme, že |EB| je rovnaká ako |AB| lebo obe sú stranami rovnostranného trojuholníka. |BC| je tiež rovnaká ako |AB|, obe sú strany štvorca. Z toho dostávame, že |EB|=|BC| a teda trojuholník EBC je rovnoramenný.
Teraz si môžeme poprenášať nejaké uhly:
Vieme, že |\angle ABE| je 60\degree kvôli rovnostrannému trojuholníku a |\angle ABC| je 90\degree kvôli štvorcu. |\angle EBC| bude teda 90\degree-60\degree=30\degree

Do rovnoramenného trojuholníka EBC si môžeme dorátať uhly pri základni - vieme, že oba sú rovnaké a spolu s |\angle EBC| majú súčet 180\degree, teda dostávame 2|\angle EBC|+30\degree=180\degree. Čo vyriešime a dostaneme |\angle EBC|=75\degree. Zo zadania je |CE| = |FE|, teda trojuholník CEF je rovnoramenný tiež, kvôli tomu sa uhly pri jeho základni rovnajú - 75\degree si môžeme preniesť aj na EFC.

Uhol CEB je rozdelený na dve časti zo súčtom 75\degree, dopočítame si deda |\angle CEF| a |\angle FEB| už zistíme ľahko.
V trojuholníku CEF už poznáme dva uhly, teda tretí je: 180\degree-75\degree-75\degree=30\degree. Uhol FEB je jeho doplnkom do 75\degree, teda je 75\degree-30\degree=45\degree.

Odpoveď: |\angle FEB| = 45\degree
7. príklad
Pri hre dvoch hráčov, to vždy vyzerá podobne. Vyberieme si hráča pre ktorého sa budeme snažiť odkázať, že má víťaznú stratégiu (ak si myslíme, že taký hráč existuje, ak nie, tak pre oboch hráčov sa snažíme ukázať, že majú stratégiu neprehrávajúcu). Tú opíšeme a potom sa pozeráme na druhého hráča a snažíme sa zistiť, či neexistuje ťah, niečo čím by to mohol prvému hráčovi prekaziť.
Vyhrávajúcu stratégiu má v tomto prípade prvý hráč (nemusí to tak byť vždy), čiže Pierre. Jedna z možných stretégií je nasledovná:
Prvý ťah
Pierre si v prvom ťahu zoberie číslo 5.
Druhý ťah
Pierre si v druhom ťahu zoberie číslo 7.
Tu sa musíme zaraziť. Môže si vždy Pierre zobrať v druhom ťahu číslo 7? Stratégia je návod, ktorý nám hovorí, čo má hráč pre ktorého stratégiu opisujeme robiť v každej hernej situácii do ktorej sa vie dostať. Ak by si Mária zobrala vo svojom ťahu číslo 7, tak je Pierre bezradný. Musíme mu povedať, čo má robiť.
Pokiaľ si Mária zobrala číslo 7, tak si Pierre zoberie číslo 3.
Vieme sa rýchlo zamyslieť, či si Pierre číslo 3 zobrať môže, no určite áno, keďže on má 5 a v tomto prípade má Mária 7. Trojka je voľná.
Máme teda dva prípady, ktoré si musíme rozobrať.
Tretí ťah
Pierre má čísla 5 a 7. Ak si zoberie hociktoré z čísel 3,6 a 9, tak vyhral. Mária však zatiaľ mala iba dva ťahy, takže Pierrovi aspoň jedno z týchto čísiel ostáva a vie si ho zobrať a tým vyhrať.
Ostáva rozobrať druhý prípad.
Pierre má čísla 5 a 3. Ak si zoberie hociktoré z čísel 1,4 a 7, tak vyhral. Mária však rovnako ako v predchádzajúcom prípade mala zatiaľ iba dva ťahy, takže Pierre vie aj v tomto prípade vyhrať.
Týmto sme ukázali, že nech Mária bude robiť, čokoľvek, tak Pierre po troch ťahoch vyhrá. Ostáva otázka, či by Mária nemohla vyhrať skôr? Tu je to jasné, no ak by to Pierrovi mala trvať výhra napríklad štyri ťahy, už to je legitímna otázka.
Takže nakoniec poznamenajme, že Márii sa nemôže podariť skôr vytvoriť aritmetickú postupnosť o dĺžke 3 ako Pierrovi. Kým sa Mária dostane ku svojmu tretiemu ťahu, tak Pierre vyhrá.
Takto by teda vedelo vyzerať úplne správne riešenie bez zbytočných poznámok:
Vyhrávajúcu stratégiu má prvý hráč, čiže Pierre. Jedna z možných stretégií je nasledovná:
Prvý ťah
Pierre si v prvom ťahu zoberie číslo 5.
Druhý ťah
- Pokiaľ je voľné číslo 7, tak si ho Pierre zoberie.
- Pokiaľ si Mária zobrala číslo 7, tak si Pierre zoberie číslo 3.
Tretí ťah
- Pierre má čísla 5 a 7. Ak si zoberie hociktoré z čísel 3,6 a 9, tak vyhral. Mária však zatiaľ mala iba dva ťahy, takže Pierrovi aspoň jedno z týchto čísiel ostáva a vie si ho zobrať a tým vyhrať.
- Pierre má čísla 5 a 3. Ak si zoberie hociktoré z čísel 1,4 a 7, tak vyhral. Mária však rovnako ako v predchádzajúcom prípade mala zatiaľ iba dva ťahy, takže Pierre vie aj v tomto prípade vyhrať.
Nakoniec poznamenajme, že Márii sa nemôže podariť skôr vytvoriť aritmetickú postupnosť o dĺžke 3. Kým sa Mária dostane ku svojmu tretiemu ťahu, tak Pierre vyhrá.
Komentár
Je nutné aby Pierrovi stratégia hovorila, čo má robiť ak Mária spraví čokoľvek. Čo má Pierre spraviť, ak si Mária zoberie práve 4? Občas s tým je pri niektorých aj dobrých riešeniach problém. Často ostávajú okrajové prípady, ktoré riešenie neošetruje. Riešenia často používajú argument, že pre druhého hráča je niečo najlepšie. Napríklad v našom riešení by sme mohli povedať, že Mária bude blokovať čísla 3,6 a 9 takže si zoberie dve z nich a ani to nebude stačiť. Tu je to relatívne jasné, no ako vieme, že blokovanie je to najlepšie čo môže spraviť, ak to nevedie ani k remíze? Neexistujú ťahy, ktoré by k výhre viedli, napríklad, to že si Mária zoberie 2? To musí byť z riešenia jasné.
8. príklad
Najprv si uvedomme dve vlastnosti NSD:
c \cdot NSD(a,b) = NSD(c\cdot a,c\cdot b)
Táto rovnica platí preto, že ak NSD(a,b)=k tak vieme a vyjadriť ako x \cdot k a b vyjadriť ako y \cdot k pričom x a y sú nesúdelitelné. Potom c \cdot a = c \cdot x \cdot k a c \cdot b = c \cdot y \cdot k, takže NSD(c\cdot a,c\cdot b) = NSD(c\cdot x \cdot k,c\cdot y \cdot k) a kedže x a y sú nesúdeliteľné tak sa táto rovnica bude rovnať c \cdot k. Na druhej strane máme c \cdot NSD(a,b) a kedže vieme, že NSD(a,b)=k tak táto rovnica sa bude tiež rovnať c \cdot k.
NSD(NSD(a,b), NSD(c,d)) = NSD(a,b,c,d)
Pre túto rovnicu si povedzme, že NSD(a,b)=k a NSD(c,d)=l potom rovnako ako v predošlej rovnici si vyjadríme čísla a, b, c, d pomocou spoločných deliteľov a zapíšeme si ich do pravej časti rovnice NSD(x \cdot k, y \cdot k, z \cdot l, w \cdot l), kedže x,y sú nesúdeliteľné tak ani jedna z nich sa nenachádza vo výsledku a to isté platí o z, w, takže táto NSD sa bude rovnať NSD(k,l), čo si môžeme všimnúť že je také isté ako na ľavej strane.
Teraz sa poďme pozrieť na dôkaz:
Rovnicu dokážeme tak, že si vezmeme jednu stranu rovnice a budeme ju upravovať, dokým nebude rovnaká ako druhá strana rovnice. Pri takomto spôsobe si však treba dať pozor, aby sme upravovali iba túto jednu stranu, teda napríklad nemôžeme nič prirátavať, ale ani násobiť a podobne.
Takže, vezmime si ľavú stranu rovnice:
NSD(a,c) \cdot NSD(a,d)
Tu použijeme jednu z vlastností, ktorú sme uviedli na začiatku zadania, a to tú prvú:
NSD(NSD(a,c) \cdot a, NSD(a,c)\cdot d)
Všimnime si, že sme len obe čísla v NSD(a,d) vynásobili výrazom NSD(a,c). Vieme si však všimnúť, že ten istý trik vieme použiť znova, a dostať a a d do vnútra zátvoriek:
NSD(NSD(a \cdot a,a\cdot c),NSD(d \cdot a,d \cdot c))
Teraz použijeme druhú vlastnosť, ktorú sme na začiatku uviedli. Vidíme, že máme veľa NSD v sebe, a tak ich môžeme zjednodušiť do jednej, ako v príklade na začiatku:
NSD(a\cdot a,a\cdot c,d \cdot a,d\cdot c)
Pozrime sa na posledný člen tohoto NSD. Je to c \cdot d, a my zo zadania vieme, že c\cdot d=a \cdot b, a teda v tomto výraze môžeme c\cdot d nahradiť a\cdot b.
NSD(a\cdot a,a \cdot c,a \cdot d,a \cdot b)
Tu vieme opäť použiť prvú vlastnosť NSD, pretože každý člen násobíme a, a teda ho môžeme vyňať pred NSD.
a\cdot NSD(a,c,d,b) = a \cdot NSD(a,b,c,d)
No, a vidíme, že sme sa iba úpravami ľavej strany rovnice dostali k pravej, a teda sme rovnosť dokázali.
Komentár
Veľa z vás malo problém skutočne popísať a dokázať vaše riešenie, a často ste urobili nejakú drobnú chybičku alebo predpoklad, prípadne ste nejakú vec jednoducho zle dokázali. Za toto sme strhli väčšinu bodov. Dobrý tip do budúcna je, že pri dokazovacích príkladoch je takmer vždy lepšie si veci zapísať matematicky, vo výrazoch.
9. príklad
V zadaní bolo napísané Dokážte pre ľubovoľné kladné celé k. Najprv si teda povedzme, čo takéto zadanie znamená a ako sa takéto úlohy riešia.
Ak máme nejaké tvrdenie dokázať pre ľubovoľné číslo (alebo čokoľvek iné, napríklad ľubovoľné usporiadanie tabuľky, ľubovoľné rozloženie figúrok...), nestačí si vybrať jedno číslo, napríklad k = 2 a ukázať, že pre tento prípad tvrdenie platí. Treba prejsť všetky prípady, od k = 1, k = 2, ..., k = \frac{n}{2}. Ak je týchto prípadov nejaký konkrétny počet, tak to naozaj môžeme dokazovať tak, že prejdeme každú možnosť a ukážeme, že tvrdenie vždy platí (napríklad ak by sme mali zadané, že n \le 10, tak nám zostane iba päť možností na k a môžeme prejsť všetky). Ako ale prejsť všetky prípady, keď nevieme, koľko ich je, alebo je ich dokonca nekonečno?
Najčastejší spôsob, ktorým sa takéto úlohy riešia je, že sa pozrieme na to, čo majú všetky možnosti spoločné a ukážeme z toho, že tvrdenie platí. Keďže pri tom vychádzame z toho, čo majú všetky možnosti spoločné, mohli by sme prejsť všetky možnosti a toto zdôvodnenie použiť pri každej. Teda síce nevieme prejsť všetky možnosti posupne, ale môžeme sa takto "pozrieť na všetky naraz".
Na začiatku máme jednu živú baktériu. Môžeme si ju nakreslit takto:

Teraz povedzme, že by sa tá baktéria rozmnožila. Tým ona umrie, ale vzniknú dve nové. Môžeme si to nakresliť:

Živé baktérie kreslím zelenou a mŕtve červenou. Povedzme, že by sa teraz jedna z tých dvoch živých baktérií rozmnožila.

Takto môžeme kresliť ďalej, až sa dostaneme ku konečnému obrázku, ktorý môže vyzerať napríklad takto:

Na konkrétnom umiestnení baktérií nezáleží, dôležité je, že každá baktéria je spojená nahor s baktériou, z ktorej vznikla. Môžeme si všimnúť, že každá červená baktéria má dve "deti". Počet potomkov nejakej baktérie môžeme zistiť tak, že sa pozrieme na to, koľko je zelených baktérií, ktoré sú niekde pod ňou (nie nutne priamo spojené s ňou, môžu byť spojené cez niektoré ďalšie, ale iba smerom dole).
Preto keď máme jednu baktériu, ktorá sa rozdelila na dve, tak počet jej potomkov je súčet počtov potomkov tých dvoch baktérií, ktoré vznikli jej rozmnožením (napríklad ak sa jedna baktéria rozmnožila na dve, z ktorých jedna má troch potomkov a druhá štyroch, tak táto má sedem).
Máme teda takýto obrázok, kde je n zelených baktérií. Chceli by sme teda nájsť nejakú takú, ktorá má aspoň k a najviac 2k potomkov. Ako by sme ju mohli nájsť?
Je ľahké nájsť baktériu, ktorá má aspoň k potomkov - môžeme napríklad zobrať tú prvú, ktorá je na vrchu nášho obrázka. Ak by mala zároveň najviac 2k potomkov, tak výborne - našli sme ju. Ak má viac, ako 2k potomkov, musíme hľadať ďalej - nájsť nejakú baktériu, ktorá má menej potomkov, ako ona. Vieme, že jej dve "deti" majú dokopy toľko potomkov, ako ona, teda viac, ako 2k. Preto aspoň jeden z nich musí mať viac, ako k potomkov (ak by obaja mali najviac k, tak ich súčet je najviac 2k). Takže ak sa pozrieme na to jej "dieťa", ktoré má viac potomkov, tak sme našli baktériu, ktorá má menej potomkov, ako tá, ktorú sme našli predtým, ale stále aspoň k.
Ak má táto baktéria najviac 2k potomkov, tak sme ju našli. Ak má viac, tak sa môžeme pozrieť na jej deti, ak ani medzi nimi nenájdeme, tak na deti ich detí a tak ďalej. Takto nájdeme baktérie, ktoré majú stále menej a menej potomkov, ale stále aspoň k. Keďže čísel medzi k a n je iba nejaký obmedzený počet, nemôžeme zmenšovať donekonečna a určite raz nájdeme takú baktériu, akú hľadáme. Taktiež sa nám nestane, že by baktéria už nemala deti, lebo ak má viac, ako 2k potomkov (najmenej troch, keďže k \ge 1), tak sa musela ešte niekedy rozmnožovať.
Tento dôkaz funguje vždy rovnako bez ohľadu na výber n a k a bez ohľadu na poradie delenia baktérií. Preto sme ukázali, že pre každé n a k spĺňajúce podmienky zo zadania existuje baktéria s aspoň k a najviac 2k potomkami.
10. príklad
Pri geometrii nie je iná cesta, ako si na začiatok nakresliť obrázok. V riešení budeme používať niekoľko vedomostí. Najprv, súčet uhlov v trojuholníku je 180\degreea jednoduché dôsledky, ako napríklad to, že rovnostranný trojuholník má všetky uhly veľké 60\degree. Na druhej strane v tomto príklade budeme veľa pracovať s Tálesovou vetou. Tá hovorí, že pokiaľ máme na kružnici body A,B,C, tak úsečka AC tvorí jej priemer práve vtedy keď \lvert\angle ABC \rvert= 90\degree. Pokiaľ si sa ňou ešte nestretol/la, tak predtým ako budeš pokračovať ti odporúčam si prečítať Wikipédiu. Nakoniec budeme potrebovať zhodné trojuholníky.
Riešenie rozdelíme do niekoľkých fází. Prvým krokom je ukázať, že uhol \angle BXC je pravý. Postupne si všimnime, že \lvert\angle DCF\rvert=\lvert\angle CBE\rvert = 60\degree, keďže sú to uhly pri vrcholoch rovnostranných trojuholníkov. Ďalej ako uhol pri vrchole obdĺžnika \rvert \angle DCB \rvert=90\degree. Teraz ľahko dopočítame uhly \lvert \angle BCX\rvert=180\degree-90\degree-60\degree=30\degree a uhol \lvert\angle BXC\rvert=180\degree-30\degree-60\degree=90\degree.
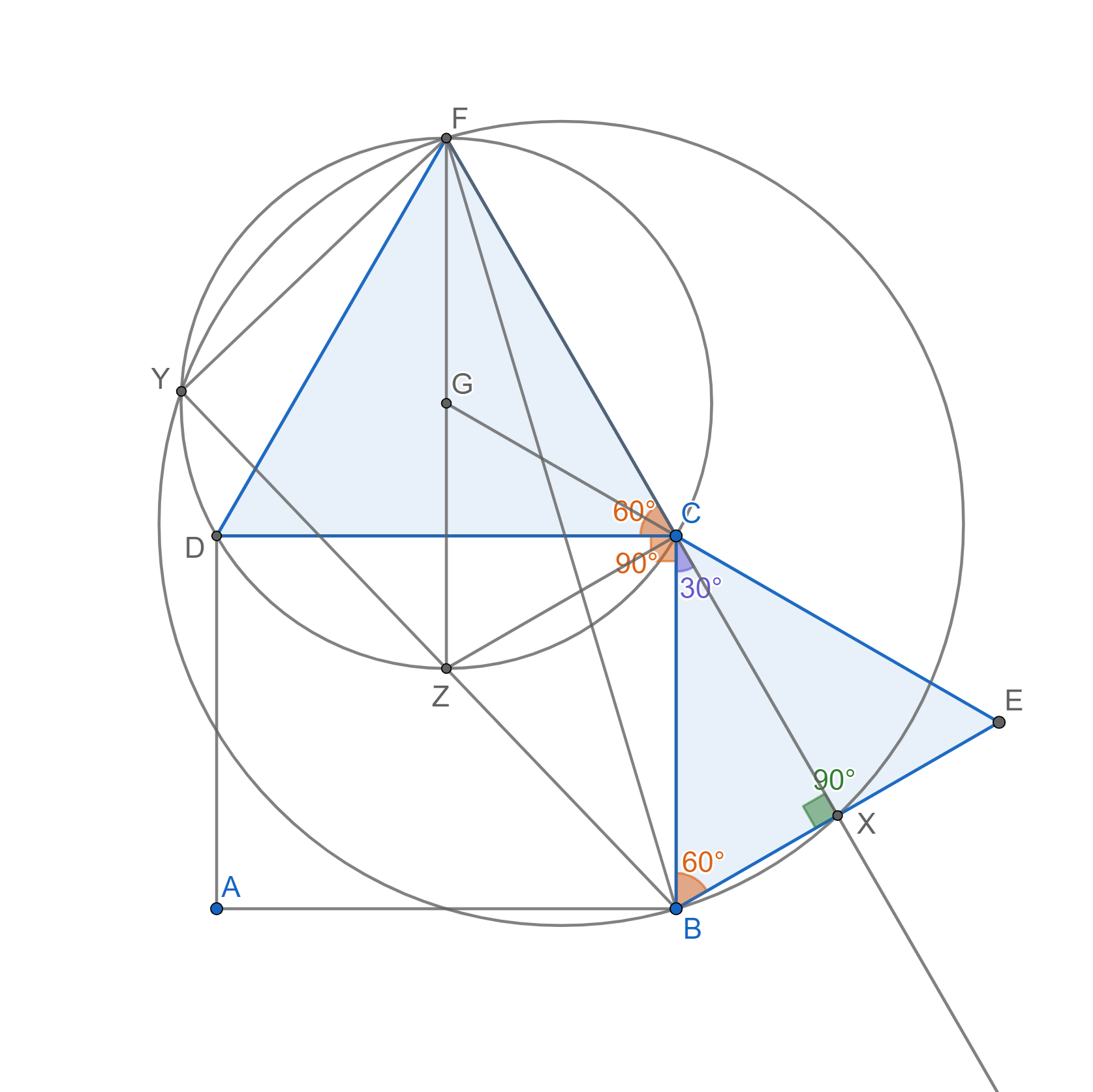
Teraz je čas použiť Tálesovu vetu. Keďže \angle BXF je pravý, tak úsečka BF tvorí priemer kružnice k_1. Potom znovu vďaka Tálesovej vete je aj uhol \angle FYB pravý.
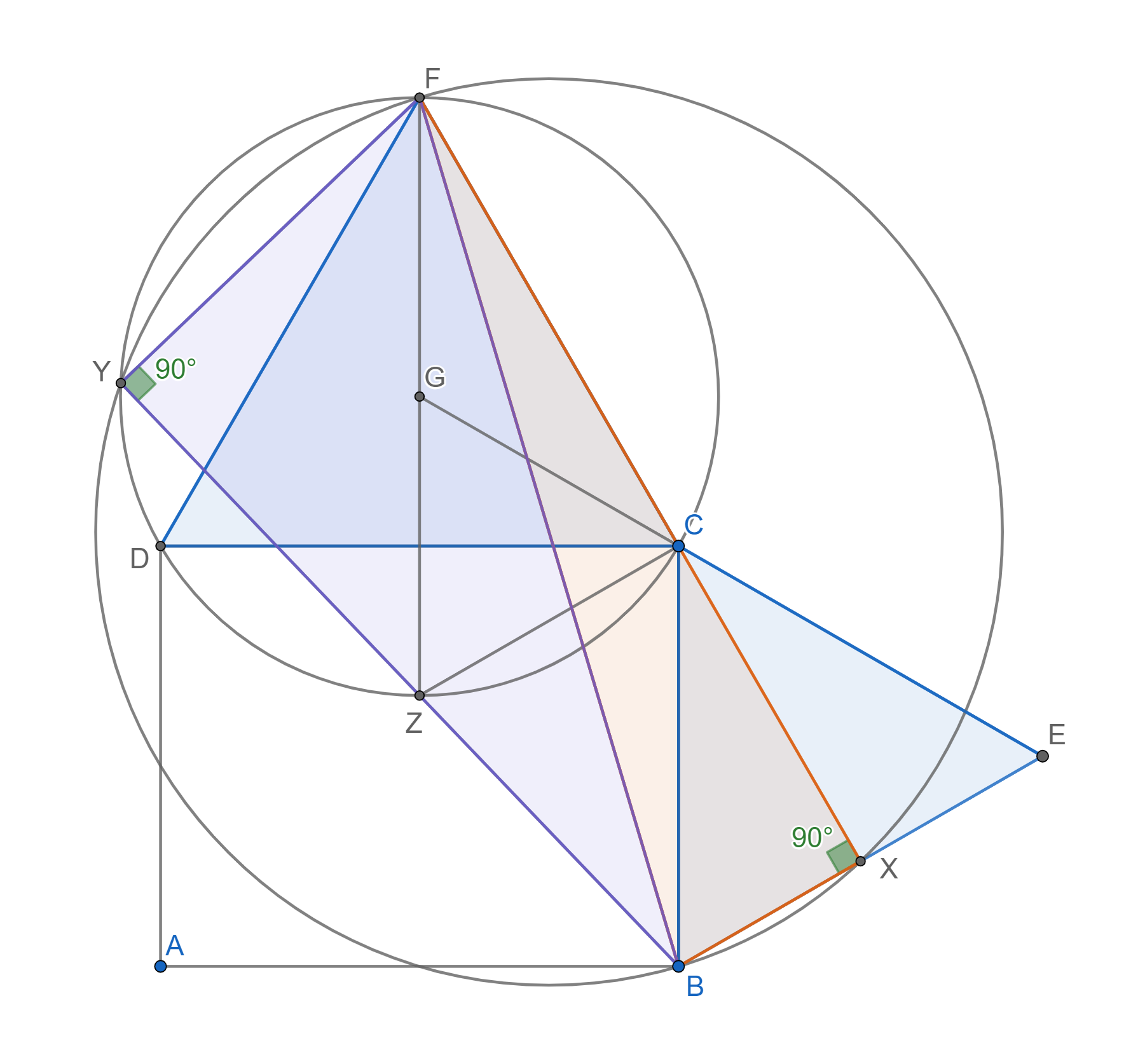
Teraz si všimnime, že body Y, Z a F ležia na kružnici opísanej trojuholníku \triangle DCF a navyše pri vrchole Y máme pravý uhol. Zas použijeme Tálesovu vetu aby sme dostali, že FZ je priemerom kružnice k_2. Ako priemer špeciálne teda prechádza cez jej stred označený ako G. Avšak v rovnostrannom trojuholníku sa stred kružnice opísanej zhoduje s priesečníkom výšok. Špecálne je teda polpriamka \overrightarrow{FG} kolmá na DC.
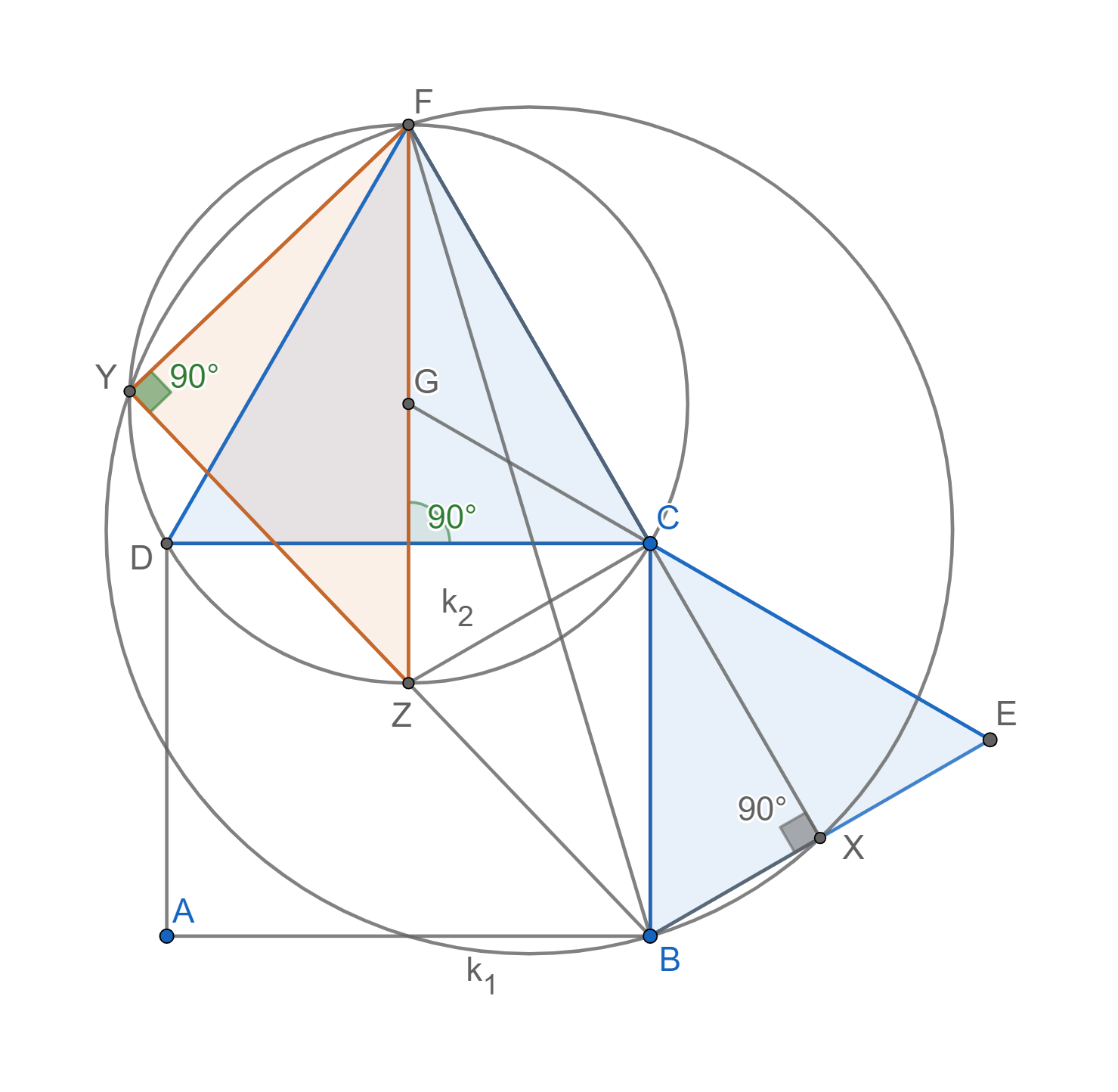
Aktuálne sa vieme zamerať na trojuholník \triangle ZCF. Už vieme, že ZF je prepona. Ide teda podľa Tálesovej vety o trojuholník pravouhlý. Spomeňme si, že \lvert \angle DCF\rvert = 60\degree. Potom ľahko dopočítame, že \lvert\angle ZCD\rvert = 30\degree.

Už sme skoro tam \lvert\angle HCG\rvert= 60/2\degree=30\degreea teraz G je stred kružnice k_2, no úsečka GZ je kolmá na DC a zároveň trojuholníky \triangle HCG a \triangle HCZ sú zhodné podľa vety sus, takže \lvert HG \rvert=\lvert HZ \rvert. G je naozaj obrazom bodu Z pri osovej súmernosti.

Teraz by sme mohli byť šťastní, no ukazuje sa, že v príklade je ešte jeden zakopaný pes. V prípade, že DC\gt\gt BC, poprípade BC\gt\gt DC (postup je úplne rovnaký a nebudeme ho uvádzať) tak trojuholník \triangle DCF vieme preklopiť aj do spodnej roviny tak, aby bod F neležal v obdĺžniku ABCD.

Avšak v tomto prípade tvrdenie zo zadania platiť nemôže, lebo bod Z je v spodnej polrovine od úsečky DC a teda nemôže byť stredom kružnice opísanej FCD. Máte pravdu prísne vzaté to nie je dôkaz :), ale je to jasné.