Vzorové riešenia 1. kola

Pre lepšiu predstavu budú vo vzorovom riešení uvedené schémy, ktoré znázorňujú poradie zvieratok. Zvieratá budu označené veľkým začiatočným písmenom (napr. krava je K ) a podčiarkovník ( \_ ) znázorňuje miesto, kde ešte nie je žiadne zviera.

Túto úlohu môžeme riešiť tak, že sa pozrieme na jednotlivé podmienky a porozmýšľame, ako nám ovplyvňujú poradie, v akom sú zvieratká zaočkované. Samozrejme, môžeme začať s akoukoľvek podmienkou, ale najednoduchšie bude, ak začneme so štvrtou, ktorá znie takto:

Krava musí byť zaočkovaná skôr ako ovca.

Tým, že krava musí byť zaočkovaná skôr ako ovca, môžeme usúdiť, že ovca určite nebude zaočkovaná prvá. Ak by bola, tak krava nemôže byť zaočkovaná pred ovcou. Presuňme sa teda na ďalšiu podmienku. Teraz sa pozrieme na tretiu, ktorá znie veľmi podobne:

Ovca môže byť zaočkovaná až potom ako je zaočkovaný zajac alebo pes.

Ako aj pri štvrtej podmienke, pred tým, než je zaočkovaná ovca, musí byť zaočkovaný pes alebo zajac (alebo obaja). To znamená, že ovca nemôže byť ani na druhom mieste, pretože pred ovcou musí byť aj krava, aj aspoň jedno zo zvyšných zvieratiek.

Máme 2​ situácie:

• ovca je tretia: \_ \; \_ O \; \_
• ovca je štvrtá: \_ \; \_ \; \_ \; O

Najskôr vyriešme na situáciu, kde ovca je štvrtá ( \_ \; \_ \; \_ \; O ). Pozrime sa na prvú podmienku, ktorá znie takto:

Ak je zajac zaočkovaný skôr ako ovca, potom musí byť pes zaočkovaný posledný.

Ovca je zaočkovaná posledná, takže zajac bude určite zaočkovaný pred ovcou a tým pádom podľa prvej podmienky pes musí byť zaočkovaný ako posledný. Ale už ovca je na poslednom mieste. To znamená, že ovca nemôže byť štvrtá, lebo je to v rozpore s prvou podmienkou.

Druhá situácia je, že ovca je zaočkovaná ako tretia ( \_ \; \_ \; O \; \_ ). Pozrime sa na štvrté miesto, kto na ňom môže byť? Môže tam byť buď pes alebo zajac, krava nie, pretože musí byť zaočkovaná pred ovcou (4​. podmienka).

Najskôr sa pozrieme na prípad, že zajac je na 4​. mieste ( \_ \; \_ \; O \; Z ). Teraz využijeme druhú podmienku:

Zajac môže byť zaočkovaný neskôr ako pes iba v prípade, že krava bude zaočkovaná až po zajacovi.

Zajac je posledný, to znamená, že je určite zaočkovaný neskôr ako pes, ale zároveň, tým že je posledný nemôže byť krava zaočkovaná po ňom. Vzniká nám spor a tým pádom zajac nemôže byť na štvrtom mieste.

Ak je pes na štvrtom mieste ( \_ \; \_ \; O \; P ), vieme zvyšné zvieratká doplniť len 2 spôsobmi ( Z \; K \; O \; P a K \; Z \; O \; P). Keďže sú to jediné 2​ možnosti, ktoré pripadajú do úvahy, stačí len skúškou správnosti overiť, či vôbec vyhovujú všetkým podmienkam. A po skúške je zrejmé, že toto sú jediné poradia vyhovujúce všetkým podmienkam.

Odpoveď

Sú dve môžnosti v akých Louis Pasteur môže zaočkovať svoje zvieratká: Z \; K \; O \; P a K \; Z \; O \; P

Najlepší postup pri riešení tejto úlohy je si postupne prechádzať otázky a odpovede a určiť všetko čo z nich vyplýva. Pri každej otázke totiž existujú čísla, pri ktorých by odpovedali inak ako “neviem”. Pri číslach ktoré určite nespĺňajú podmienku z otázky (bez ohľadu na to, aké z možných čísel má ten druhý) by odpovedali nie. O takýchto číslach potom vieme povedať, že ich určite mať nemôžu, a s touto vedomosťou sa nám znížia možnosti aj pri ďalšej otázke.

Mária sa v prvej otázke pýta: „Je tvoje číslo dvojnásobok môjho?“ a Pierre odpovie „Neviem“.
Aby Pierrovo číslo mohlo byť dvojnásobkom Máriinho, muselo by byť párne, pretože všetky dvojnásobky sú párne. Ak by jeho číslo bolo nepárne, isto by vedel, že nie je dvojnásobkom Máriinho a preto by povedal “nie”. Z toho vyplýva, že Pierre nemôže mať nepárne, a teda musí mať párne číslo.

V druhej otázke sa Pierre pýta Márie: „Je tvoje číslo dvojnásobok môjho?“ a Mária odpovie „Neviem“.
Mária už vie, že Pierre má párne číslo, čiže otázku môže interpretovať ako: „Je tvoje číslo byť dvojnásobok môjho párneho čísla?“ Čísla, ktoré sú dvojnásobkom párneho čísla sú v podstate násobky štvorky (čiže 2*2=4​, 4*2=8​, 6*2=12​,...14*2=28​). Keď Mária odpovie „neviem“, znamená to, že jej číslo je jedným z násobkov štvorky pod 30​. Ak by nebolo, mohla by s istotou povedať „nie“.

V tretej otázke sa Mária pýta: „Je tvoje číslo polovica môjho?“ a Pierre jej odpovie „Neviem“.
Mária aj Pierre vedia, že Mária musí mať násobok štvorky. Pierre svojou odpoveďou povedal, že jeho číslo je niektoré z Máriiných násobkov štvorky zmenšených o polovicu. Jeho čísla teda môžu byť 28:2=14​, 24:2=12​… (čiže párne čísla do 15​). Kebyže je číslo väčšie ako 15​, jeho dvojnásobok by bol väčší ako 30​, čo Mária nemôže mať podľa pravidiel hry a musel by odpovedať „nie“.

Vo štvrtej otázke sa Pierre opýta Márie: „Je tvoje číslo polovica môjho?“ a ona odpovie „Neviem“.
Vieme, že Pierre má niektoré z párnych čísel menších ako 15​. Pierre teraz od Márie zistil, že jej číslo je jedno z polovíc jeho čísel. To sú konkrétne celé čísla pod 7​ vrátane (čiže 1​, 2​, 3​,...7​). Kebyže je jej číslo väčšie ako 7​, jeho dvojnásobok by musel byť väčší ako 15​. Lenže my vieme, že jeho dvojnásobok – čo je Pierrovo číslo – nemôže byť väčší ako 15​.

V tomto momente už Pierre vie povedať, aké je Máriino číslo. Vie dve dôležité informácie:

1. Máriino číslo je násobkom štvorky. Čo zistil po druhej otázke.
2. Máriino číslo je niektoré z celých čísel menších alebo rovných 7​. To vie po štvrtej otázke. 
   

​Keď sa na to pozrieme, Máriino číslo musí spĺňať obe tieto podmienky naraz. Také číslo je len jedno a je to práve číslo 4​. Je to násobok štvorky a taktiež je menšie alebo rovné 7​.

​Odpoveď: 

Máriino číslo je 4. 

Vieme, že stroj môže buď od celého stĺpca odčítať 1​, alebo celý riadok vynásobiť 2​. Na začiatok je dôležité uvedomiť si, že ak sa nám podarí dostať nejaké políčko na 0​, odčítaním v danom stĺpci sa nám táto 0​ zmení na záporné číslo. Avšak ak by sme vynásobili riadok, v ktorom sa toto políčko nachádza, s touto 0​ by sa nič nestalo. Tým pádom vieme, že chceme políčka v tabuľke nulovať postupne po stĺpcoch. Ak dostaneme v celom stĺpci samé 0​, odčítavať od neho už nemusíme a násobením sa nám nezmení. 

Ďalej si treba dávať pozor na to, aby sme sa odčítavaním nedostali do záporných čísel. Odtiaľ sa už totiž nikdy nevieme dostať na 0​, pretože odčítavaním sa číslo bude stále zmenšovať, a ak by sme záporné číslo vynásobili 2​, taktiež by sme išli iba viac do záporu. Z toho vyplýva, že všetky políčka v jednom stĺpci musíme dostať na 0​ naraz, keďže ak by 0​ nebola vo všetkých, čísla väčšie ako 0​ by sme museli zmenšiť odčítaním, čím by sme ale z núl dostali záporné čísla. V jednom stĺpci tak najprv musíme dostať do všetkých políčok rovnaké čísla.

Ako dostať v stĺpci rovnaké čísla?

Pozrime sa na príklad nejakého jedného stĺpca. Keďže v celej tabuľke máme na začiatku kladné celé čísla, ostatné stĺpce nás teraz zaujímať nemusia keďže odčítavaním v tom našom stĺpci ich meniť nebudeme. Ak by sme nejaký riadok násobili 2​, v stĺpcoch s kladnými číslami zostanú kladné a v už vynulových nuly.

Krok 1: Teraz môžeme od stĺpca odčítavať , až kým sa nám v nejakom políčku neobjaví 1​. Ak by sme odčítali aj vtedy, v tomto políčku by sme dostali 0 a zvyšné by sme už nemohli zmenšovať. Dostaneme napríklad:

Krok 2: Ako som už ukázali, odčítavať kvôli políčkam s jednotkami nemôžeme. Neostáva nám nič iné, ako vynásobiť všetky políčka, v ktorých je 1​.

Keďže 1*1=2, krokom 2 sme vlastne ku vybraným políčkam pripočítali 1​. Tým pádom môžeme opäť odčítavať od celého stĺpca. Teraz nám už len stačí striedať krok 1 a krok 2. Postupne totiž zmenšujeme všetky čísla, ktoré sme ešte nikdy nedostali na 1​, keďže riadky v ktorých sa tieto čísla nachádzajú nemusíme násobiť a čísla, ktoré sme už niekedy dostali na 1​, krokom 2 zväčšíme na 2​ a potom krokom 1 opäť na 1​. Toto môžeme robiť, až kým odčítavaním nedostaneme do všetkých políčok 1​. Vtedy už môžme spokojne odčítať a budeme mať vynulovaný celý stĺpec a presúvame sa na ďalší stĺpec.

Keďže čísla v ďalšom stĺpci, ktorý sa rozhodneme nulovať sa mohli iba zväčšiť, postupným opakovaním krokov 1 a 2 sa nám podarí vynulovať aj tento stĺpec a napokon aj všetky zvyšné.

Pozrime sa na túto úlohu od konca. Keď má hráč pred svojím ťahom napísané číslo, z ktorého sa vie dostať na 1887, pridá číslo, ktorým sa dostane na 1887 a vyhráva. 

944 je prvé také číslo, lebo 944+943=1887. Číslo 943 je ešte málo, lebo z 943 sa vieme dostať maximálne na 943+942=1885. Môžme si všimnúť, že 943 sa dá dostať len na čísla od 944  do 1885 ​(943+1  až 943+942) , teda len čísla, z ktorých sa dá vyhrať. Z toho vyplíva, že ten, kto má teda pred svojím ťahom 943​ prehral.

Teraz zopakujeme ten istý postup, len s tým, že sa nepotrebujeme dostať na číslo 1887, ale len na číslo 943, lebo sme ukázali, že ak sa dostaneme na 943, už sa vieme zaručene dostať aj na 1887.​

472 je prvé číslo, z ktorého sa dá dostať na 943, lebo 472+471=943. Číslo 471 je ešte málo, lebo 471+470=941. Zo 471 sa dá teda dostať len na čísla 472 až 941, teda len na čísla, z ktorých sa dostaneme na 943 a odtiaľ už vyhrať vieme.

Teraz máme znovu rovnakú úlohu, len sa nám stačí vedieť dostať na 471 a potom už vyhrať vieme.

Tento postup ešte niekoľkokrát zopakujeme a dostaneme sa k tomu, že sa postupne potrebujeme dostať na čísla 3,7,14,29,58,117,235,471,943 a potom vyhráme napísaním 1887

Zo žiadneho z týchto čísel sa súper nevie dostať na nasledujúce, alebo vyššie, lebo nasledujúce číslo je aspoň dvakrát väčšie, než predchádzajúce a druhý hráč vie pripočítať maximálne číslo o 1 menšie, než terajšie číslo, teda jedným ťahom nevie číslo zdvojnásobiť.

Taktiež ku každému číslu musí súper vždy prirátať aspoň 1 a potom sa vieme dostať na nasledujúce číslo(4+3=7, 8+6=14,15+14=29,30+28=58,59+58=117,118+117=235,236+235=471,472+471=943,944+943=1887)

Týmto sme dokázali, že výhernú stratégiu má hráč, ktorý napíše číslo 3, lebo potom vie napísať na nasledujúci ťah vždy nasledujúce číslo v rade a teda aj 1887.

Keďže začína Tesla a na papieri je napísané číslo 2, vie prirátať 1 a zvýšiť číslo na 3 a potom už len navyšuje vždy na nasledujúce číslo v rade a tak napíše 1887 a vyhrá.​

Odpoveď:

Víťaznú stratégiu má prvý hráč, čiže Tesla.

Zamyslime sa najprv ako si vieme naše zadanie nejako rozumne zapísať. Po sebe idúce čísla vždy stúpajú o 1​. Takže ak by to prvé bolo x​, tak potom Schrödingerovské číslo bude vyzerať takto:

x+(x+1)+(x+2)+(x+3)+(x+4)+(x+5)+(x+6)+(x+7)+(x+8)​

T​oto vieme ľahko upraviť na 9x+36 = 9 \cdot (x + 4)​. Z takéhoto tvaru vidíme, že každé Schrödingerovské číslo bude deliteľné \textbf 9.

Bohrovské číslo vieme podobne zapísať pre ľubovoľné prirodzené y​ ako: 

y+(y+1)+(y+2)+(y+3)+(y+4)+(y+5)+(y+6)+(y+7)+(y+8)+(y+9) = 10y+45 = 5 \cdot (2y + 9)​

Teda každé Bohrovské číslo musí byť deliteľné 5​. Ak sa pozrieme ešte na predošlú úpravu, 10y + 45​, všimneme si, že keďže 10y​ bude mať vždy na mieste jednotiek cifru 0​ a číslo 45​ tam bude mať vždy cifru 5​, tak Bohrovské číslo musí mať na mieste jednotiek cifru \textbf 5​. Inými slovami, keďže zátvorka (2y + 9)​ bude vždy nepárna, Bohrovské číslo bude vždy nepárnym násobkom 5​.

Planckovské číslo vieme pre ľubovoľné prirodzené z​ zapísať ako: 

z+(z+1)+(z+2)+(z+3)+(z+4)+(z+5)+(z+6)+(z+7)+(z+8) +(z+9)+(z+10) = 11z+55 = 11 \cdot (z + 5)​. 

Z čoho vidíme, že Planckovské číslo bude deliteľné \textbf {11}​. 

Zhrňme si teda podmienky, ktoré musí spĺňať číslo v superpozícii:

• bude deliteľné 9​

• bude mať na mieste jednotiek 5​

• bude deliteľné 11​

Čísla, ktoré toto splnia majú šancu byť v superpozícii. Najmenšie také číslo je najmenší spoločný násobok 5​, 9​ a 11​, ktorý je 495​. Vidíme, že čísla sú nesúdeliteľné, a teda ich najmenší spoločný násobok bude ich súčinom. Musíme si však ešte overiť, že číslo 495​ je skutočne v superpozícii, keďže nie všetky spoločné násobky 5​, 9​ a 11​ budú spĺňať zadanie (990 = 2 \cdot 5 \cdot 9 \cdot 11​ napríklad nie je Bohrovské, keďže nekončí 5​).

Ako teda nájdeme 9​, 10​ a 11​ čísel, ktorých súčet vie byť 495​? Využijeme rovnice, čo máme vyššie:

495 = 9x + 36 = 10y + 45 = 11z + 55​. Keďže vieme nájsť celé x = 51​, y = 45, z = 40​ tak číslo 495​ môžeme považovať za vyhovujúce zadaniu. Menšie už nie je, keďže neexistuje menšie číslo, ktoré je deliteľné 5​, 9​ a 11​ zároveň.

Iné riešenie

Tri najmenšie Schrödingerovské čísla sú 1+2+3+4+5+6+7+8+9=45​, 2+3+4+5+6+7+8+9+10=54 a 3+4+5+6+7+8+9+10+11=63​. Z toho si môžeme všimnúť, že vyzerá, že každé ďalšie číslo bude o 9​ väčšie ako to prechádzajúce. Zamyslime sa nad tým aký je rozdiel medzi dvomi po sebe idúcimi Schrödingerovskými číslami. 

Ak máme nejaké Schrödingerovské číslo tvaru x+(x+1)+(x+2)+(x+3)+(x+4)+(x+5)+(x+6)+(x+7)+(x+8)​, tak najbližšie väčšie Schrödingerovské číslo je (x+1)+(x+2)+(x+3)+(x+4)+(x+5)+(x+6)+(x+7)+(x+8)+(x+9)​. Z toho odčítaním týchto dvoch výrazov vidíme, že rozdiel medzi dvomi po sebe idúcimi Schrödingerovskými číslami je vždy -x+(x+9)=9​. Teda keďže najmenšie Schrödingerovské číslo je deliteľné 9​ a každé väčšie číslo je o 9​ väčšie, tak každé Schrödingerovské číslo bude deliteľné \textbf 9​.

Analogicky to platí pre 10​ a 11​. Pri 10​ nám ale vyjde, že máme zvyšok 5​. Týmpádom máme ukázanú deliteľnosť číslami 9​, 5​, 11​ a ďalej  už postupujeme ako popísané vyššie až kým sa nedopracujeme k číslu 495. Opäť je je na konci riešenia potrebná skúška.

Iné riešenie

K sčítavaniu po sebe idúcich čísel od n​ po  n+k môžeme pristupovať aj pomocou vzorca na výpočet k po sebe idúcich čísel ktorý vyzerá nasledovne:

k \cdot {\frac {(n)+(n+k)} {2}}​​

Môžme si do tohto vzroca napríklad dosadiť Schrödingerovské číslo ktoré je súčtom čísel od n po n+8​
:

9 \cdot {\frac {(n)+(n+8)} {2}} = {\frac {18n+72} {2}} = 9n + 36 = 9 \cdot (n + 4)​, z čoho opäť vieme vidieť deliteľnosť 9​. Analogicky vieme spraviť niečo podobné aj pre 10​ a 11. Ďalej už vieme postupujeme ako popísané vyššie. Opäť je na konci riešenia potrebná skúška.

Kľúč k vyriešeniu príkladu bude v zameraní sa na najväčšie a najmenšie číslo. V každom správne vyplnenom štvorci musí existovať nejaké najväčšie číslo a nejaké najmenšie číslo.

Pozrime sa na to bližšie zápisom. Urobme si tvrdenie, že n je najväčšie číslo. Vieme, že ak je nejaké číslo aritmetickým priemerom dvoch čísel, tak jeho vzdialenosť na číselnej osi od oboch týchto čísel je rovnaká.

V správne vyplnenom štvorci ho teda musíme dostať aritmetickým priemerom jeho susedov, teda n = {\frac {(n-x)+(n+x)} {2}}, pričom (n + x) a (n-x) sú niektorí jeho susedia. Ak je však x iné ako 0, tak buď (n -x) alebo (n +x) budú väčšie ako n​, čo je spor s tvrdením, že n je najväčšie číslo. Takto sme dokázali, že x = 0. Inými slovami, najväčšie číslo v štvorci (n) môžeme dostať len tak, že urobíme aritmetický priemer jeho dvoch susedov, ktorí sú tiež n.

Všimnime si, že rovnaké tvrdenie sa dá dokázať aj pre najmenšie číslo, a to presne takým istým postupom.

V našom štvorci to znamená, že každé najväčšie číslo n musí susediť s aspoň dvoma číslami n, a rovnako každé najmenšie číslo m musí susediť s aspoň dvoma číslami m. 

Takto vieme zistiť, že v každom štvorci budú aspoň tri najväčšie čísla n. Vieme našu podmienku splniť pre všetky tri? Nie, pretože v štvorčekovej sieti platí, že pre ľubovoľné políčko nie sú žiadni jeho susedia navzájom susední. Teda, mohli by sme podmienku splniť pre jedno políčko s n, avšak jeho susedné políčka s n​ nedokážu byť navzájom susedné.

Čo ak by sme jedno políčko s n pridali? Potom by sme ich už vedeli usporiadať, aby bola splnená podmienka, teda aby každé n susedilo s dvoma inými n, a to takto:

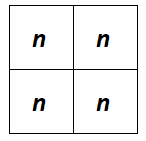
Čo sme si teraz ukázali? Tento náš postup nám dokázal, že pre ľubovoľne správne vyplnený štvorec musí byť počet políčok s najväčším číslom aspoň 4. Rovnaký postup vieme aplikovať pre najmenšie číslo, a teda nám vyjde, že v ľubovoľnom správne vyplnenom štvorci musia byť aspoň 4 políčka s najväčším číslom n a aspoň 4 políčka s najmenším číslom m.

Vieme teda, že aspoň 8​ políčok bude zabratých týmito číslami. Keďže sa pýtame na najväčší počet rôznych čísel v štvorci, tak v ak by sa nám zvyšných 56​ políčok podarilo vyplniť navzájom rôznymi číslami, určite to bude najlepšie riešenie. Dá sa to?

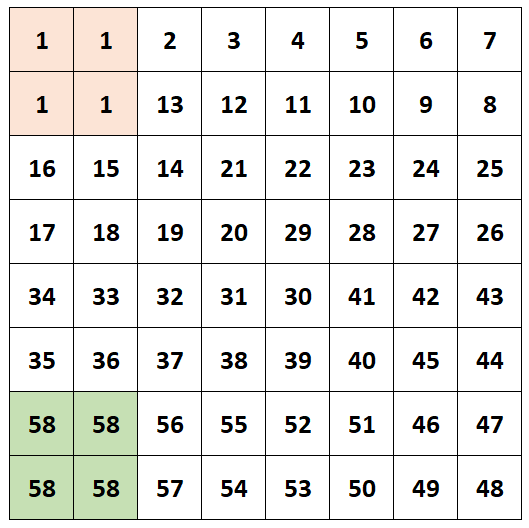
Vyznačené políčka sú políčka s najväčším číslom a políčka s najmenším číslom. Zvyšné políčka sú všetky rôzne, a teda sme našli určite najlepšie riešenie. V tomto riešení máme 58 rôznych čísel. 

Nejaká konkrétna konštrukcia sa dala nájsť tak že sme nakreslili ťah, ktorý prechádzal všetkými políčkami okrem minima a maxima tak, že začínal políčkom s najmenším číslom a končil políčkom s najväčším číslom. každé políčko tohto ťahu malo číslo vždy o 1 väčšie ako predošlé políčko. Týmto sme zariadili žepre každé políčko s číslom x​ platí, že má určite dvoch susedov ktorí majú čísla x-1 a x+1 a ich priemer teda je x​​

Vieme, že D je stredom strany CA a zároveň úsečky AF a AD sú rovnako dlhé, teda \vert CD \vert = \vert DA \vert = \vert AF \vert.

Označme \vert \sphericalangle ADF \vert = \alpha. Trojuholník ADF je rovnoramenný so základňou DF, preto \vert \sphericalangle AFD \vert = \vert \sphericalangle ADF \vert = \alpha. Uhly CDE a AFB sú susedné k uhlom ADF a AFD. Preto ​\vert \sphericalangle CDE \vert = 180 \degree - \vert \sphericalangle ADF \vert =180 \degree - \alpha a tiež \vert \sphericalangle AFB \vert = 180 \degree - \vert \sphericalangle AFD \vert =180 \degree - \alpha.

Keďže zo zadania \vert DF \vert = \vert BE \vert, tak aj \vert DE \vert = \vert DF \vert + \vert FE \vert = \vert BE \vert + \vert FE \vert = \vert FB \vert.

Teraz už vieme, že \vert CD \vert = \vert AF \vert, \vert \sphericalangle CDE \vert = 180 \degree - \alpha = \vert \sphericalangle AFB \vert, \vert DE \vert = \vert FB \vert. Teda trojuholníky ​CDE a AFB sú zhodné podľa vety sus (strana, uhol, strana). Preto aj \vert CE \vert = \vert AB \vert = 1.​

Odpoveď: Dĺžka úsečky CE je 1.​

Vo vzorovom riešení budeme využívať rozšírený Dirichletov princíp. Ak máme n pretmetov k typov, tak existuje nejaký typ, že ho je najviac \lfloor \frac{n}{k} \rfloor predmetov a nejaký typ, ktorého je aspoň \lceil \frac{n}{k} \rceil predmetov. 

Ďalej budeme predpokladať, že kameňov je presne n rôznych farieb, pričom ak by ich v skutočnosti bolo menej ako n, tak môžene doplniť farby, ktoré budú mať 0 kameňov.

Pozrime sa na farbu A, ktorej je najmenej kameňov, počet týchto kameňov je najviac n, lebo máme n^2 kameňov a n farieb. Ďalej sa pozrime na farbu B, ktorej kameňov je najviac, počet týchto kameňov je aspoň n, lebo máme n^2 kameňov a n farieb. Teraz vložíme všetky kamene farby A a všetky voľné miesta doplníme kameňmi farby B. Toto bude vždy možné, lebo kapacita jednej krabice je n a kameňov farby A je najviac n a kameňov farby B je aspoň n.

Zbavili sme sa n kameňov, 1 farby a 1 krabice, takže nám ostáva n(n-1) kameňov, n-1 farieb a n-1 krabíc. Znovu môžeme zopakovať popísaný proces, lebo farby, ktorej kameňov je najmenej je najviac n a farby, ktorej je najviac kameňov je aspoň n kameňov. Znovu sa zbavíme n kameňov, 1 farby a 1 krabice, ostane nám n(n-2) kameňov, n-2 farieb a n-2 krabíc.

Tento proces môžeme opakovať kým sa nám neminú všetky kamene, lebo po vykonaní tohto procesu k-krát budeme mať n(n-k) kameňov, n-k farieb a n-k krabíc. Teda stále bude platiť, že farby ktorej kameňov je najmenej je najviac n a farby, ktorej je najviac kameňov je aspoň n kameňov. Takže stále sa budeme môcť pomocou každej krabice zbaviť n kameňov a jednej farby.