Vzorové riešenia 2. kola
1. príklad
Na konci bude na parkovisku 6 kužilasov. Tie budú zaberať spolu 6 \cdot 3=18 parkovacích miest, nech už zaparkovali akokoľvek. Teda, keď chceme zistiť koľko najviac miest mohlo mať parkovisko, chceme vlastne zistiť, koľko najviac miest mohlo zostať voľných. Rozdelíme si parkovisko na tri časti.
Vľavo, pred prvým na začiatku zaparkovaným kružilasom, sú 4 voľné miesta. Tam sa zmestí kružilas, teda jeden tam bude musieť zaparkovať. Potom tam zostane už len jedno prázdne miesto, kde už nikto parkovať nemôže.
Vpravo, za druhým na začiatku zaparkovaným kružilasom, je 7 voľných miest. Tam sa zmestí kružilas, teda aspoň jeden tam musel potom zaparkovať. Keďže chceme, aby zostalo čo najviac parkovacích miest voľných, páčilo by sa nám, keby tam kružilasov parkovalo čo najmenej. A ten jeden kružilas naozaj stačí. Môže totiž zaparkovať priamo do stredu týchto siedmich miest. Napravo aj naľavo od neho budú tak len dve voľné miesta, kde už ďalší kružilas zaparkovať nemôže. Teda spolu v tejto časti môžu zostať voľné najviac 4 parkovacie miesta.
Koľko najviac voľných políčok môže zostať v zóne medzi pôvodnými dvoma kružilasmi? Zostali nám ešte dva kružilasy, ktoré tam chceme umiestniť. Medzi každými dvoma kružilasmi môže byť medzera najviac 2 políčka, inak by sa tam zmestil medzi ne ďalší. Teda po pridaní zvyšných dvoch kružilasov máme v strede tri medzery medzi štyrma kružilasmi a každá má najviac dve parkovacie miesta. To je spolu 3\cdot2=6 voľných miest.
Teraz už len stačí sčítať počet miest ktoré zaberajú kružilasy, najväčší možný počet voľných miest vľavo, najväčší možný počet voľných miest vpravo a najväčší možný počet voľných miest v strede. To je 18+1+4+6=29. Na obrázku vidíme, ako napríklad mohli kružilasy zaparkovať. Modré stoja na svojom mieste od začiatku, zelené sú tie, ktoré prišli neskôr.
Odpoveď: Na parkovisku môže byť najviac 29 miest.
2. príklad
V zadaní máme 3-, 4- a 5-ciferný palindróm. Zapíšme si ich ako súčet:
\begin{array}{ccccc} & & A & B & A \\ +& C& D & D & C\\ \hline E & F & G & F & E\end{array}
Rovnaké písmenká predstavujú rovnaké cifry. Ako teraz začať riešiť? Najlepšie bude si skúsiť dosadiť náhodné čísla a takýmto spôsobom si vieme veľmi pekne všimnúť niečo, čo sa nám ďalej pri riešení vie zísť.
Napríklad si všimneme, že ak C \lt 9, tak aj ak by sme A a B a D volili najväčšie možné, čiže 9, súčet by nebol 5-ciferný, ako môžeme vidieť tu:
\begin{array}{ccccc} & & 9 & 9 & 9 \\ +& 8 & 9 & 9 & 8\\ \hline & 9 & 9 & 9 & 7\end{array}
Takto sme hneď zistili, že C=9. Okrem toho sme si ale všimli ešte jednu dôležitú vec, že prechod cez desiatku bude vždy 0, alebo 1. Prečo?
Ak máme na mieste jednotiek ľubovoľné 2 cifry, tak dokopy budú maximálne 9+9=18. Takže nám môže "zostať" najviac 1. Pre desiatky, sa nám k tomu tá jednotka pripletie, takže máme 1+9+9=19. Ale prechod bude stále 1. Pre stovky a vyššie pozície sa situácia zopakuje. Vieme si to povšimnúť aj na súčte 2 čísel zložených zo samých 9.
\begin{array}{ccccc} & 9 & 9 & 9 \\ +& 9 & 9 & 9\\ \hline 1 & 1+8 & 1+8 & 8\end{array}
Poďme to teraz pekne zužitkovať. E je aspoň 1, inak by nešlo o 5-ciferné číslo. Potom k C musíme niečo prirátať aby sme sa dostali cez desiatku. Avšak už vieme, že prechod je maximálne 1. Takže k C nič väčšie ako 1 prirátať nemôžme. Keďže 1+9=10, tak rovno vidíme, aj že F=0. Tieto pozorovania teraz doplňme do nášho súčtu:
\begin{array}{ccccc} & & A & B & A \\ +& 9& D & D & C\\ \hline 1 & 0 & G & F & E\end{array}
Všetky čísla v súčte sa čítajú rovnako odpredu ako odzadu, takže naše pozorovania vieme preklopiť aj na miesta jednotiek a desiatok:
\begin{array}{ccccc} & & A & B & A \\ +& 9& D & D & 9\\ \hline 1 & 0 & G & 0 & 1\end{array}
Teraz nie je ťažké dopočítať A. Hľadáme číslo, ku ktorému ak pripočítame 9, tak tento súčet bude mať na mieste jednotiek 1. Hľadané číslo A = 2:
\begin{array}{ccccc} & & 2 & B & 2 \\ +& 9& D & D & 9\\ \hline 1 & 0 & G & 0 & 1\end{array}
Poďme sa pozrieť na D. V tomto bode, je celkom dobrá cesta aj skúšanie, je to iba 9 možností, avšak vieme si to ešte zjednodušiť na 3.
Spomenieme si, že prvé dve cifry sú 10. Aby sme ich dosiahli, tak k 9 potrebujeme prirátať 1. Teda D musí zabezpečiť prechod cez desiatku. Ak je D menej ako 7, tak sa nám to určite nepodarí, lebo 6+2+1=9, a to je málo. Poďme postupne vyskúšať ostávajúce 3 možnosti.
D môže byť postupne 9,\, 8 a 7 a z toho ľahko dopočítame G a B.
| D | súčet | B | G | výsledok |
|---|---|---|---|---|
| 9 | \begin{array}{ccccc} & & 2 & B & 2 \\ +& 9& 9 & 9 & 9\\ \hline 1 & 0 & G & 0 & 1\end{array} | 0 | 2 | \begin{array}{ccccc} & & 2 & 0 & 2 \\ +& 9& 9 & 9 & 9\\ \hline 1 & 0 & 2 & 0 & 1\end{array} |
| 8 | \begin{array}{ccccc} & & 2 & B & 2 \\ +& 9& 8 & 8 & 9\\ \hline 1 & 0 & G & 0 & 1\end{array} | 1 | 1 | \begin{array}{ccccc} & & 2 & 1 & 2 \\ +& 9& 8 & 8 & 9\\ \hline 1 & 0 & 1 & 0 & 1\end{array} |
| 7 | \begin{array}{ccccc} & & 2 & B & 2 \\ +& 9& 7 & 7 & 9\\ \hline 1 & 0 & G & 0 & 1\end{array} | 2 | 0 | \begin{array}{ccccc} & & 2 & 2 & 2 \\ +& 9& 7 & 7 & 9\\ \hline 1 & 0 & 0 & 0 & 1\end{array} |
Odpoveď: Možné palindrómy sú uvedené vyššie v tabuľke.
Komentár
Vo vašich riešeniach sme často nenachádzali vysvetlenie k tvrdeniam, ktoré neboli vždy úplne očividné. Napríklad, bez ukázania, že prechod je najviac 1, alebo, že 999 + 8998 = 9997, nemá zmysel tvrdiť, že C = 9. Takisto bez 999 + 9999 = 10 998 by sme nemali usúdiť, že prvé dvojčíslie výsledku je 10.
Ďalšou kľúčovou časťou tejto úlohy bola skúška správnosti, a teda overenie si, či sa nájdené palindrómy po sčítaní naozaj rovnajú päťcifernému palindrómu. Celkovo nás ale veľmi teší, že väčšina z vás sa dopracovala aspoň k časti riešenia - ste šikovní 🐬
3. príklad
Keďže súčin je aj pri dvoch číslach zvyčajne väčší ako súčet, hľadať budeme pomerne nízke čísla, ktoré by mohli byť počtami dier. Začneme teda s čo najviac nulami, skúsime jednotky a tak ďalej, až kým sa nám nebude zdať súčin vždy príliš veľký. Potom sa pokúsime zdôvodniť, že bude naozaj príliš veľký. Počas rozoberania možností nás zaujíma iba, koľkokrát sa ktoré číslo objaví, keďže na poradí nezáleží.
Ak sa v čísle nachádza 0, súčin bude určite 0, a teda, aby bol aj súčet 0, musia byť aj všetky ostatné čísla nuly. Teda máme jednu odpoveď, 0, 0, 0, 0, a prešli sme všetky možnosti s nulami.
Ak sa v čísle nachádzajú tri jednotky (a viac), tak nech je posledné číslo akékoľvek (nazvime ho x), súčin je 1\cdot1\cdot1\cdot x a súčet je 1+1+1+x. Avšak x=3\cdot x nebude nikdy sedieť, teda toto riešením nebude.
Ak sa v čísle nachádzajú 2 jednotky, tretie číslo (nazvime ho x) môže byť 2, vtedy hľadáme posledné číslo tak aby platilo 1\cdot1\cdot2\cdot y=1+1+2+y, teda 2\cdot y=4+y po odčítaní y dáva y=4. Dostali sme možnosť 1, 1, 2, 4.
Ešte môžeme mať obe čísla x a y väčšie ako 2, vtedy máme aspoň 1+1+3+3=8 a 1\cdot1\cdot3\cdot3=9. Tu vidíme že je už súčin vyšší ako súčet. Zároveň vieme ukázať, že aj pri všetkých ďalších kombináciách to tak bude. Vždy keď zvýšime jedno z x a y o 1, súčet sa zvýši o 1 a súčin sa zvýši o to druhé číslo (napr. x\cdot(y+1)=x\cdot y+x pri zvýšení y o 1). Vieme, že obe čísla sú väčšie ako 1, takže sa súčin zvýši viac ako súčet. Nech teda hocikoľko takýchto “krokov” so zvýšením o 1 urobíme, nikdy súčet nemôže dobehnúť súčin. Takýmito krokmi vieme z pôvodných 1, 1, 3, 3 urobiť hocijaké číslo s dvomi jednotkami ktoré neobsahuje dvojku, teda žiadne nebude riešením.
Ak sa v čísle nachádza najviac 1 jednotka, najmenší prípad čo môžeme mať je 1,2,2,2. Vtedy je súčet 7 ale súčin 8. Znova použijeme podobnú úvahu ako v predošlom prípade, aby sme ukázali že žiadne takéto riešenia nebudú. Zvýšením čísla o 1 dostaneme o 1 vyšší súčet, no súčin bude vo všeobecnom prípade a \cdot b \cdot c \cdot (d+1) = a \cdot b \cdot c \cdot d+a \cdot b \cdot c, inak povedané zvýši sa o súčin zvyšných čísel. Keďže všetky čísla až na jedno sú aspoň 2, súčin troch z nich bude vždy viac ako 1. Tiež teda každým zvýšením iba vzdialime súčin od súčtu, bude ešte väčší. Takto sa vieme dostať ku každej kombinácii s jednou jednotkou alebo so žiadnou.
Ukázali sme teda, že jediné riešenia sú 0,0,0,0 a 1,1,2,4.
Iné riešenie
hľadáme štyri čísla pre ktoré platí a+b+c+d=a \cdot b \cdot c \cdot d. Pričom a bude najväčšie z nich. Súčet teda určite nepresiahne 4a, nemôže ho teda presiahnuť ani súčin. Teda 4a \geq a \cdot b \cdot c \cdot d, čo, ak a > 0, môžeme vydeliť a a dostaneme 4 \geq b \cdot c \cdot d. Jediné kombinácie ktoré vyhovujú (vždy zoradené od najmenšieho čísla) si rozoberieme v tabuľke, a dopočítame a:
| b, c, d | súčet = súčin | výpočet a | je to riešenie? |
|---|---|---|---|
| 1, 1, 1 | a+3=a | 3=0 | nepravda |
| 1, 1, 2 | a+4=2a | a=4 | sedí |
| 1, 1, 3 | a+5=3a | 5/2=a | nie je celé |
| 1, 1, 4 | a+6=4a | 2=a | a nie je najväčšie; riešenie máme vyššie |
| 1, 2, 2 | a+5=4a | 5/3=a | nie je celé |
Ešte ostala možnosť kedy je niektoré číslo 0. Vtedy je aj celkový súčin 0. To sa môže súčtu rovnať iba vtedy, keď sčítavame samé nuly, teda dostávame dve riešenia: 0, 0, 0, 0 a 1, 1, 2, 4.
Komentár
Najnáročnejšou časťou riešenia sa javilo preskúmať väčšie možnosti (cca od 1, 2, 2, 2). Keď povieme, že vždy pri vyšších bude súčin príliš veľký, musíme to zdôvodniť. Teda povedať, čo všetko sú "vyššie" kombinácie, a ukázať aj dôvod, prečo sa nemôže nikdy súčet zvýšiť viac, a presiahnuť súčin.
Bodovanie
Vo väčšine postupov riešitelia rozoberali prípady podobne ako vo vzorovom riešení, vtedy sme udeľovali:
3 body za nájdenie možnosti 0, 0, 0, 0 a správne vysvetlené vylúčenie možností s iba nulami a jednotkami.
4 body za nájdenie možnosti 1, 1, 2, 4 a vylúčenie ostatných možností s aspoň 2 jednotkami.
3 body za vylúčenie všetkých ostatných možností.
4. príklad
Najprv sa pozrime na Slovákov 2. výrok: „Zo zvyšných dvoch z nás je jeden klamár a jeden pravdovravný.“ Podľa tohto výroku vieme, že ak by Slovák hovoril pravdu, tak Američan alebo Rus musí hovoriť pravdu a ten druhý z nich musí klamať. Ak by Slovák klamal, tak buď Američan aj Rus hovoria pravdu alebo obaja klamú. Možnosť v ktorej klamú všetci traja môžeme hneď vylúčiť, lebo zadanie hovorí, že aspoň jeden hovorí pravdu. Ostali nám 3 možnosti. Poďme ich vyskúšať:
Američan a Rus hovoria pravdu, Slovák klame.
Rus hovorí, že 3. cifra je 1 a to, že v čísle nie je väčšia cifra ako tá posledná. Takže na poslednom mieste môže byť buď 0 alebo 1. Slovák hovorí, že posledná cifra je párna, ale klame. Takže posledná cifra musí byť nepárna a teda na poslednom mieste bude 1. Američan hovorí, že v čísle sú aspoň 2 cifry prvočísla. Vidíme, že 3. ani 4. cifra prvočísla nie sú, preto naše prvé dve cifry musia byť prvočísla ktorých súčet je 11. (Podľa 1. Američanovho výroku.) Existujú ale takéto prvočísla? Keďže 11 je nepárne číslo, tak jedno z týchto hľadaných prvočísel musí byť párne a druhé nepárne. Jediné párne prvočíslo je 2. Potom druhá hľadaná cifra by mala byť 11-2=9. Avšak vieme, že 9 prvočíslo nie je a teda táto možnosť nemá riešenie.
Američan a Slovák hovoria pravdu, Rus klame.
Slovák hovorí, že 1. cifra je 4. Američan hovorí, že súčet prvých dvoch cifier je 11, takže druhá cifra musí byť 7. Ďalej Američan hovorí, že 3. cifra má byť menšia ako 2, čiže nám na výber ostali 1 \text{ a } 0. Vieme, že Rus klame keď hovorí, že 3. cifra je 1. Tým pádom 3. cifra bude 0. Posledná cifra musí byť prvočíslo, lebo Američan hovorí, že v čísle musia byť aspoň 2 prvočísla. Takisto musí byť posledná cifra párna, to nám zase hovorí Slovák. Jediné párne prvočíslo je 2, takže na poslednom mieste bude 2. Vyšiel nám pin 4702.
Ostáva nám spraviť skúšku, aby sme zistili, či toto číslo naozaj spĺňa všetky výroky. Američan sedí: Súčet prvých dvoch cifier je 11, 3. cifra je menšia ako 2, v čísle sú 2 prvočísla. Rus tiež sedí: 3. cifra nie je 1, posledná cifra nie je najmenšia. Slovák takisto sedí: 1. cifra je 4, Američan hovorí pravdu a Rus klame, posledná cifra je párna. Máme jedno riešenie, teraz sa poďme pozrieť na poslednú možnosť.
Rus a Slovák hovoria pravdu, Američan klame.
Rus hovorí, že 3. cifra je 1. Američan hovorí, že 3. cifra je menšia ako 2. Avšak tento Američanov výrok je pravdivý, ale Američan nemôže hovoriť pravdu a to je spor. Takže táto možnosť nevedie k riešeniu.
Hľadané číslo je 4702. Ostatné možnosti ako môžu hovoriť pravdu alebo klamať nie sú správne, lebo by nebol splnený Slovákov 2. výrok.
Odpoveď: Ich pin je 4702.
Komentár
Väčšina z vás zvládla príklad dobre a vyskytli sa iba malé chyby. Veľa z vás nedostatočne zdôvodnilo prečo neexistujú 2 prvočísla, ktorých súčet je 11. Takisto ste veľmi často zabudli poriadne zdôvodniť niektorý z dôležitých krokov, za čo sme strhávali body. Tiež by sme chceli pripomenúť, že pri takomto type príkladu sa po nájdení vyhovujúcej možnosti oplatí urobiť skúšku, aby ste si overili, či sú všetky výroky zo zadania splnené.
5. príklad
Ako prvé si môžeme všimnúť, že po ťahu každého z hráčov sa počet hadov v kruhu zmenší o 1. Keďže počet hadov je 2021, čo je nepárne číslo, tak medzi Merlinom a Mackerom bude na začiatku z jednej strany párny počet hadov a z druhej nepárny počet hadov, pretože iba súčtom párneho a nepárneho čísla vieme dostať nepárne číslo.
Teraz sa pozrime na to, čo sa stane po prvom ťahu oboch hráčov. Ak Merlin zhodí hada zo strany, kde je ich párny počet, bude medzi nimi z oboch strán nepárny počet. Potom nech Macker zhodí akéhokoľvek hada bude medzi nimi z jednej strany párny a z druhej nepárny počet hadov. Ak Merlin zhodí hada zo strany, kde je ich nepárny počet, bude medzi nimi z oboch strán párny počet. Po Mackerovom ťahu potom bude medzi nimi znova z jednej strany párny a z druhej nepárny počet hadov. Všimnime si, že v oboch prípadoch sme sa po ťahoch oboch hráčov dostali do podobnej situácie ako na začiatku, len s 2019 hadmi.
Zamyslime sa teraz, kedy niektorí z nich prehráva. Na to, aby napríklad Merlina mohol Macker zhodiť, musí medzi nimi z jednej strany byť 0 hadov, keď sa Macker dostane na ťah. Všimnime si, že 0 je párne číslo.
Ako sme už ukázali, Merlin sa dostane na ťah vždy v situácii, že z jednej strany je medzi ním a Mackerom párny počet hadov a z druhej nepárny. Potom si vie vždy vybrať či po jeho ťahu bude medzi nimi z oboch strán párny počet alebo nepárny počet hadov. Teda vie zabezpečiť aby sa Macker dostal na ťah v situácii, že je medzi nimi z oboch strán nepárny počet hadov, a teda ani jeden z týchto počtov nemôže byť nula. Macker teda nemôže vyhrať, takže vždy vyhráva Merlin.
6. príklad
Kým koniec stíhačky dobehne Mackera, stihne Macker prejsť 30\,\text{m}. Zo zadania vieme, že Macker a Merlin idú rovnakou rýchlosťou, Merlin teda za ten istý čas prejde tiež 30\,\text{m}. Potom stihne prejsť ešte 15\,\text{m}, kým ho koniec stíhačky dobehne. Koniec stíhačky za ten čas, čo Merlin prejde týchto 15\,\text{m}, prejde 75\,\text{m} (koniec stíhačky išiel od bodu, kde Macker zastavil, do bodu, kde Merlin a Macker začínali, a z tohto bodu ešte 45\,\text{m} k Merlinovi). Stíhačka teda ide 5-krát rýchlejšie (\frac{75\,\text{m}}{15\,\text{m}}=5). Teraz vieme, že od začiatočného bodu Merlin prejde 45\,\text{m}. Vieme, že predok stíhačky prejde 5-krát viac, takže 225\,\text{m}. Koniec stíhačky prešiel od začiatku do bodu, kedy zastavil Merlina 45\,\text{m}. Stíhačka má teda (225\,\text{m}-45\,\text{m}) 180 metrov.
Iné riešenie
Tento príklad sa dá vypočítať aj vďaka vzorcu v=\frac{s}{t}, kde v je rýchlosť, s je prejdená vzdialenosť a t je čas. Určíme si, že v_s bude rýchlosť stíhačky, v_m rýchlosť Merlina a Mackera, a dĺžka stíhačky bude d.
Za nejaký čas prejde Merlin 45\,\text{m} (t=\frac{45\,\text{m}}{v_m}). Za ten istý čas stíhačka prejde svoju dĺžku a navyše ešte 45\,\text{m} (t=\tfrac{(45\,\text{m}+d)}{v_s}). Vznikli nám dve rovnice, ktoré vieme dať do rovnosti.
\dfrac{45\,\text{m}}{v_m}=\dfrac{(d+45\,\text{m})}{v_s}\\ \dfrac{v_s}{v_m}=\dfrac{(d+45\,\text{m})}{45\,\text{m}}
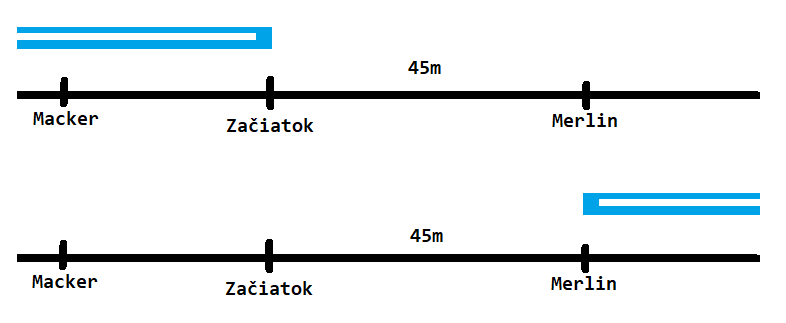
Za nejaký iný čas prejde Macker 30\,\text{m} (t'=\frac{30}{v_m}). Za tento čas prejde stíhačka svoju dĺžku bez 30\,\text{m}, ktoré išiel Macker naproti (t'=\tfrac{(d-30\,\text{m})}{v_s}).
\dfrac{30\,\text{m}}{v_m}=\dfrac{(d-30)}{v_s}\\ \dfrac{v_s}{v_m}=\dfrac{(d-30\,\text{m})}{30\,\text{m}}
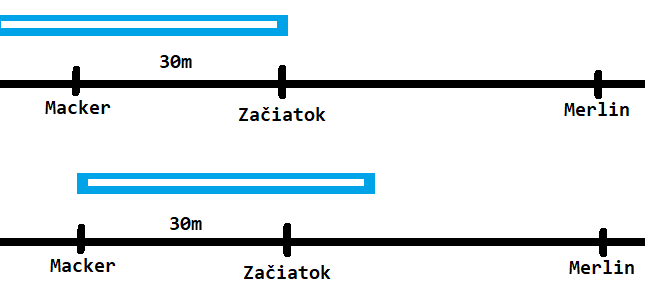
Vzťahy pre \frac{v_s}{v_m} si vieme dať do rovnosti a zistíme dĺžku stíhačky d.
\dfrac{(d+45\,\text{m})}{45\,\text{m}}=\dfrac{(d-30\,\text{m})}{30\,\text{m}}\\ 30(d+45\,\text{m}) = 45(d-30\,\text{m})\\ 30d+1350\,\text{m} = 45d-1350\,\text{m}\\ 2700\,\text{m} = 15d\\ 180\,\text{m} = d
Odpoveď: Stíhačka je dlhá 180\,\text{m}.
7. príklad
Cifry počtov Arabov si označíme A, B, C a keďže sú rôzne, tak nech pre ne platí A \gt B \gt C. Vieme z nich vytvoriť 6 rôznych čísel - ABC, ACB, BAC, BCA, CAB a CBA.
Pri porovnávaní týchto čísel začneme s cifrou na mieste stoviek. Takže čísla s prvou cifrou A budú najväčšie, čísla s prvou cifrou B budú menšie a čísla s prvou cifrou C budú najmenšie. Čísla s prvou rovnakou cifrou vieme porovnať pomocou 2. cifry. Čísla s druhou cifrou A budú väčšie ako s druhou cifrou B alebo C a čísla s druhou cifrou B budú väčšie ako čísla s druhou cifrou C. Takže počty Arabov sú zoradené nasledovne: ABC \gt ACB \gt BAC \gt BCA \gt CAB \gt CBA.
Keďže priemerný počet Arabov je počas šiestich dní je 370, tak celkový počet Arabov počas celého pobytu je 6 \cdot 370 = 2220. Počet Arabov počas celého pobytu sa ale tiež rovná:
ABC + ACB + BAC + BCA + CAB + CBA =
= (100 \cdot A+10 \cdot B+C)+(100 \cdot A+10 \cdot C+B)+(100 \cdot B+10 \cdot A+C)+(100 \cdot B+10 \cdot C+A)+(100 \cdot C+10 \cdot A+B)+(100 \cdot C+10 \cdot B+A) =
= 222 \cdot A + 222 \cdot B + 222 \cdot C
Takže dostávame: 222A+222B+222C = 2220 . Predelením 222 dostávame A + B + C = 10.
Priemerný počet Arabov za posledné tri dni je 205 a dá sa zapísať takto:
\dfrac{BCA + CAB + CBA}{3} = 205\\[8pt] \dfrac{(100 \cdot B + 10 \cdot C + A) + (100 \cdot C + 10 \cdot A + B) + (100 \cdot C + 10 \cdot B + A)}{3} = 205\\[8pt] \dfrac{111 \cdot B + 210 \cdot C + 12 \cdot A}{3} = 205\\[8pt] 37 \cdot B + 70 \cdot C + 4 \cdot A = 205\\ 33 \cdot B + 66 \cdot C + 4 \cdot (A + B + C) = 205\\ 33 \cdot B + 66 \cdot C + 40 = 205\\ 33 \cdot B + 66 \cdot C = 165\\ B + 2 \cdot C = 5
Teraz sa pozrieme na všetky hodnoty, ktoré C môže nadobúdať:
- Ak C \geq 3, tak potom 2C \geq 6 a dosadením 2C do rovnice dostaneme B + aspoň 6 = 5, čo nevyhovuje zadaniu, lebo B by muselo byť záporné.
- Ak C = 2, tak 2C = 4 a dosadením 2C do rovnice dostaneme B + 4 = 5, takže B = 1, ale to je spor s A > B > C.
- Ak C = 1, tak 2C = 2 a dosadením 2C do rovnice dostaneme B + 2 = 5, takže B = 3. Dosadením B = 3 a C = 1 do A + B + C = 10, dostaneme A + 3 + 1 = 10, takže A = 6.
Odpoveď: Počet Arabov na začiatku je 631.
Komentár
Veľa z vás v niektorej časti riešenia vyskúšalo všetky možnosi (napríklad všetky rozloženia čísel A + B + C = 10). Toto nie je zlý postup, ale u veľa z vás spôsobil chyby, keď ste zabudli prejsť niektorú možnosť (hlavne ak ste začali skôr a možností bolo viac).
8. príklad
Označme začiatočné číslo ako x. Všimnime si, že krok, v ktorom delíme číslom d nám určite nezväčší medzivýsledok (zmenší ak d \gt 1, nezmení ak d=1). Preto jediný spôsob ako zväčšiť medzivýsledok je pripočítaním k, a teda najväčšie výsledné číslo dostaneme, keď v každom kroku pripočítame k. Keďže zo zadania vieme, že najväčšie dosiahnuteľné číslo je 108, tak musí platiť x+3k=108.
Odtiaľ dostávame x=108-3k odkiaľ je jasné, že x \lt 108. Všimnime si, že pravá strana rovnice je deliteľná 3, preto x=3(36-k). Odtiaľ vidíme, že x musí byť násobkom čísla 3. Všimnime si, že toto nám hovorí, že 3 \leq x \lt 108.
Najmenšie výsledné číslo dosiahneme troma deleniami, lebo ak by sme v nejakom kroku použili namiesto delenia pripočítanie, medzivýsledok by sa zväčšil. Preto najmenšie dosiahnuteľné číslo je x:d^3 . Ak by sme vedeli, že najmenší dosiahnuteľný výsledok po troch krokoch je číslo 2, potom by sme mohli hneď povedať (rovnako ako v predchádzajúcom odseku pri najväčšom dosiahnuteľnom čísle), že platí x : d^3 =2. Toto však teraz nevieme, keďže v zadaní sa píše iba to, že číslo 2 vieme dosiahnuť.
Predpokladajme, že existujú čísla x, k, d také, že sú splnené podmienky zadania a vieme dosiahnuť výsledok 1. Najprv si všimnime že x nemôze byť 1, keďže x \geq 3. Ak by sme vedeli dosiahnuť 1 ako medzivýsledok v, znamenalo by to, že d>1, keďže dokážeme x zmenšiť. Zo zadania vieme, že všetky dosiahnuteľné výsledky sú celé kladné čísla. To je však spor s v=1 lebo v:d \lt 1. Toto nám hovorí, že ak dokážeme dosiahnuť 1, musí to byť po poslednom kroku.
Zjavne 1 je najmenší výsledok, preto sme ho museli dostať troma deleniami, teda platí x/d^3 =1, z čoho x=d^3. Keďže x musí byť násobkom čísla 3, tak aj samotné d musí byť násobkom čísla 3. Všimnime si, že ak d je viac ako 4, tak d^3 bude väčšie ako 108, čo sa nemôže stať. Preto d musí byť jedine 3, z čoho následne x=27 a dopočítaním k=27 z rovnice x+3k=108.
Vieme však s týmito číslami dosiahnuť výsledok 2, ako zadanie požaduje? Pozrime sa na to. Ak by posledný krok bolo pripočítavanie, výsledok by bol väčší ako 27, preto ak chceme dosiahnuť výsledok 2 posledný krok musí byť delenie číslom 3. Preto medzivýsledok po druhom kroku musí byť 6. Ak by druhý krok bolo pripočítavanie, tak by tento medzivýsledok bol väčší ako 27, preto druhý krok musí byť tiež delenie. Teda medzivýsledok po prvom kroku dvakrát vydelený číslom 3 nám má dať výsledok 2, to znamená, že medzivýsledok po prvom kroku musí byť 18. Keďže začiatočné číslo je 27 a v prvom kroku máme na výber ho buď deliť troma alebo k nemu pripočítať 27, tak vidíme, že hľadaný medzivýsledok 18 nevieme dostať. Vidíme tak, že pre čísla x=27, d=3, k=27 nevieme dosiahnuť výsledok 2, a preto náš predpoklad, že výsledok 1 vieme dosiahnuť musel byť nesprávny.
Predpokladali sme teda, že výsledok 1 vieme dostať, čo nás doviedlo k sporu. Preto výsledok 1 po troch krokoch dostať nemôžeme, a teda výsledok 2 je skutočne najmenší dosiahnuteľný výsledok. Preto platí x:d^3 =2, keďže najmenšie číslo dosiahneme práve troma deleniami. Z toho plynie x=2d^3. Rovnako ako vyššie, keďže x je násobok čísla 3 a musí byť menšie ako 108 (čo vyplýva z rovnice x+3k=108), tak jediné vyhovujúce d je d=3, z čoho následne dostávame x=54 a k=18. Ostáva skontrolovať, či daná trojica skutočne spĺňa všetky podmienky zadania.
Nech „d“ značí krok, v ktorom sme delili a nech „k“ značí krok, v ktorom sme pripočítavali.
| Kroky | Výsledok |
|---|---|
| k, k, k | 108 |
| k, k, d | 30 |
| k, d, k | 42 |
| d, k, k | 54 |
| k, d, d | 8 |
| d, k, d | 12 |
| d, d, k | 24 |
| d, d, d | 2 |
Vidíme tak, že všetky výsledky sú celé, pričom 108 je najväčší, a výsledok 2 bol dosiahnutý. Preto čísla x=54, d=3, k=18 vyhovujú podmienkam zadania, a teda začiatočné číslo muselo byť iba 54.
Odpoveď: Začiatočné číslo bolo 54.
Komentár
Väčšina z vás našla správny výsledok. Veľa z vás však preskočilo úvahu o tom, že 2 nemusí byť najmenšie číslo, čo značne zjednodušilo tento príklad.
9. príklad

Po chvíli pozorovania si môžeme všimnúť, že najzáhadnejší bod v zadaní je bod M. Ten leží na úsečkách TR a KA. Niečo o ňom povedať je na prvý pohľad ťažké, veď úsečka TR sama o sebe spája vrcholy dvoch rôznych rovnobežníkov. Začneme teda tým, že sa pokúsime zistiť niečo o bode M, konkrétne o jeho polohe na KA, resp. TR.
Začnime pohľadom na trojuholníky TMA a RMK. Keďže KLAT je rovnobežník, priamky TA a RK sú rovnobežné. Uhly \sphericalangle MAT a \sphericalangle MKR sú striedavé a teda rovnako veľké. Navyše uhly \sphericalangle TMA a \sphericalangle RMK sú vrcholové a tiež rovnako veľké. Trojuholníky TMA a RMK sú teda podobné podľa vety uu.
Môžeme si všimnúť, že dokážeme dokonca vypočítať aj pomer podobnosti. Vieme, že DRAK je rovnobežník, takže jeho uhlopriečky sa pretínajú v strede. Navyše aj KLAT je rovnobežník, takže protiľahlé strany sú rovnako dlhé. Odtiaľ dostávame
|TA| = |LK| = \dfrac{1}{2} |RK|.
Pomer podobnosti je teda 1:2. Platí teda napríklad |MA| = \frac{1}{2} |KM|, z čoho vieme, že |MA| = \frac{1}{3} |KA|. Podobné pozorovanie vieme urobiť aj na úsečke TR, no to ďalej v riešení nebudeme potrebovať.
Porovnajme si teraz trojuholníky TMA a TKA. Výšku na MA, resp. KA, majú spoločnú, líšia sa len dĺžky ich základní. Keďže |MA| = \frac{1}{3} |KA|, aj obsah trojuholníka TMA bude 3-krát menší ako obsah TKA. My sa však potrebujeme prepracovať až k obsahu kosoštvorca DRAK.
To však nebude problém. Úsečka KA je uhlopriečka rovnobežníka KLAT, takže ho delí na dva zhodné trojuholníky. Takže obsah trojuholníka TMA je zároveň 3-krát menší ako obsah trojuholníka KLA. Uhlopriečky rozdeľujú kosoštvorec na štyri zhodné trojuholníky. Takže obsah KLA je jednou štvrtinou obsahu kosoštvorca DRAK.
Spojíme, čo vieme a dostaneme, že obsah trojuholníka TMA je 3 \cdot 4 = 12-krát menší ako obsah kosoštvorca DRAK.
Odpoveď: Pomer obsahov kosoštvorca DRAK a trojuholníka TMA je 12:1.
Komentár
S príkladom ste sa popasovali vcelku úspešne. Najčastejšími chybami boli nejaké nevysvetlené vzťahy dĺžok, s ktorými ste pracovali. Keď napríklad využívate, že LK má polovičnú dĺžku ako RK, treba povedať, že sa uhlopriečky útvaru DRAK rozpoľujú.
Bodovanie
Za základné pozorovania o útvaroch zo zadania bolo možné získať až 2 body. Do tejto kategórie sa rátali napríklad spomínané rozpoľujúce sa uhlopriečky, kolmosť uhlopriečok útvaru DRAK, či počítanie nejakých uhlov. Viaceré z nich nebolo nutné v riešení použiť, ak ste však niečo použili a nevysvetlili, strácali ste spravidla po bode.
Ďalších 5 bodov bolo možné získať za zistenie pomeru |MA|:|KM|, prípadne pomeru obsahov trojuholníka TMA a iného trojuholníka. Tu sa postupy vcelku líšili, spravidla to však bol najzložitejší krok.
Zvyšné 3 body boli udelené za výsledné dopočítanie požadovaného pomeru.
10. príklad
Tento príklad bol fakt ťažký. Nikomu sa nepodarilo vyriešiť ho na plný počet bodov, aj keď viacerí ste od toho nemali ďaleko (fun fact: z vašich riešení by sa dokopy dalo vyskladať 10-bodové, čiže každému do úplného riešenia chýbalo niečo iné, ale na každý potrebný krok k riešeniu prišiel aspoň niekto :)).
Na druhej strane, pri takýchto príkladoch dokáže veľmi pomôcť skúsenosť a nejaká všeobecná predstava o tom, ako k takýmto príkladom vôbec pristupovať. Tento vzorák teda bude vyzerať tak, že si vysvetlíme, ako takéto úlohy riešiť vo všeobecnosti a akými úvahami sa dalo dôjsť k riešeniu. Len malá časť z toho je samotné riešenie (to, čo máte vy odovzdať), takže na konci si zhrnieme, čo z toho tvorí samotné riešenie, bez tej omáčky okolo. Ak vás zaujíma len to, môžete kľudne preskočiť až tam, ale ak ste úlohu skúšali vyriešiť a nevedeli ste si rady, môže byť fajn prečítať si to celé.
Najprv si teda poďme povedať, čo presne od nás zadanie vlastne chce.
Čo vlastne chceme spraviť?
Zadanie sa nás pýta, na koľko najmenej pokusov vieme zistiť všetky hĺbky. To znamená, že musíme vlastne spraviť dve veci:
- nájsť nejaký postup, ako tie hĺbky vieme zistiť (tomu sa hovorí konštrukcia, lebo chceme skonštruovať = nájsť riešenie), ale tiež
- overiť a dokázať, že tento spôsob je naozaj najlepší, teda že sa to nedá na menej pokusov (tomu sa hovorí dolný odhad, lebo odhadneme, koľko najmenej pokusov budeme potrebovať).
Naozaj potrebujeme obe tieto veci: ak by sme mali len konštrukciu, tak je možné, že nie je optimálna, a dá sa to aj na menej pokusov, a ak máme dolný odhad, tak nevieme, či sa na toľko pokusov naozaj dajú zistiť všetky hĺbky (len že sa to nedá na menej). Veľa z vás napríklad spravilo konštrukciu na \left\lceil 2:3 \cdot n\right\rceil (to znamená najbližšie väčšie/rovné celé číslo ako 2:3 \cdot n), ktorá fungovala, ale nebola optimálna. Na toľko pokusov by ste teda dolný odhad nenašli.
Napríklad, konštrukcia na n pokusov by mohla byť, že zistím hĺbku každej studne osobitne (ale tá nie je optimálna), a dolný odhad na 1 pokus môže byť, že keď neurobím žiadny pokus, tak predsa nič nezistím, takže je jasné, že treba aspoň jeden (ale na jeden pokus sa to väčšinou nedá spraviť). To nám moc nepovie. Keď ale máme dolný odhad aj konštrukciu na ten istý počet pokusov, vieme, že to musí byť najlepšie riešenie: na menej pokusov to nejde a na viac pokusov by to nebolo lepšie riešenie.
Vo veľa prípadoch sa konštrukcia a dolný odhad úplne líšia, takže sa oplatí vymýšľať aj písať úplne osobitne, aby bolo jasné, ktorá časť riešenia hovorí o čom. Tak, a teraz sa už pozrime na samotné riešenie tejto úlohy.
Dolný odhad
Začneme dolným odhadom. To síce väčšinou býva tá ťažšia časť riešenia, ale bez toho nevieme, na koľko krokov sa snažíme urobiť konštrukciu, takže ak aj nejakú vymyslíme, nebudeme vedieť, či je to to najlepšie riešenie. Na druhej strane, ak nájdeme dobrý dolný odhad, môžeme skúsiť k nemu vymyslieť konštrukciu, kde využijeme to, čo sme zistili pri dolnom odhade.
Chceme teda zistiť, v čom nás pravidlá skúšania obmedzujú, a z toho by sme chceli vedieť, že budeme určite potrebovať aspoň niekoľko pokusov. Čo teda môže byť problém? Vieme ľahko zistiť hodnoty všetkých hĺbok (tak, že hodíme pražce naraz do všetkých studní), ale tak nevieme od seba jednotlivé studne rozoznať. Skúsme teda prísť na to, ako musíme pražce hádzať, aby sme studne rozoznať vedeli.
Tu využijeme druhú vec, ktorú nám hovorí zadanie, že naraz musíme hádzať pražce vždy do susedných studní. To, či sú nejaké studne susedné, bude teda zjavne dôležité, tak sa pozrime na to, ako by sme dve susedné studne vedeli rozoznať. Keď sa pozeráme len na tieto dve studne, tak máme len týchto pár možností, ako vieme spraviť pokus:
- pražec nehodíme pražec ani do jednej zo studní,
- hodíme pražec do oboch studní, alebo
- hodíme pražec len do jednej z nich.
Ak by sme robili pokusy 1 a 2, tak určite studne nevieme rozoznať, lebo pri každom pokuse buď nedostaneme ani jednu z ich hĺbok, alebo obe naraz, takže nevieme, ktorá hĺbka patrí ku ktorej studni. Pre každú dvojicu susedných studní teda musíme spraviť taký pokus, že hádžeme iba do jednej z týchto studní.
Čo to ale znamená? Keďže vždy hádžeme do susedných studní, každý pokus má nejaký ľavý a pravý koniec, teda miesto medzi dvomi studňami (alebo pred prvou/za poslednou studňou), a hádžeme pražce do všetkých studní medzi týmito koncami. Môžeme si to predstaviť ako na obrázku pre n=5:
Pre každý predel (teda miesto medzi dvomi studňami alebo na kraji) teda musíme urobiť taký hod, ktorý má jeden z koncov v tomto predeli. Prečo to platí medzi studňami, sme už vysvetlili, a platí to aj na kraji, lebo ako by sa na niektorom kraji nekončil žiadny úsek, tak potom vôbec nevieme hĺbku krajnej studne.
No a čo nám toto hovorí o počte pokusov? Tak každý pokus má konce v najviac 2 nových predeloch a predelov je n + 1 (na začiatku a potom za každou studňou), takže potrebujeme aspoň (n+1):2 pokusov. Keďže počet pokusov musí byť celé číslo, tak môžeme rovno povedať, že to musí byť aspoň \left\lceil\left(n+1\right):2\right\rceil, teda najbližšie väčšie alebo rovné celé číslo.
Konštrukcia
Tak teraz už vieme, že potrebujeme aspoň toľko pokusov, skúsme teda nájsť spôsob, ako na toľko pokusov aj naozaj zistiť všetky hĺbky.
Jedna možnosť je, že využijeme to, na čo sme prišli pri dolnom odhade. Keďže každý predel musí byť ľavý alebo pravý koniec nejakého pokusu, môžeme si povedať, že napríklad ľavá polovica predelov budú ľavé konce a pravá polovica pravé konce (ak je nepárny počet predelov, nevieme ich rozdeliť na polovicu, ten v strede teda bude aj aj).
Pokusy potom budú vyzerať tak, že spojíme prvý ľavý koniec s prvým pravým, druhý ľavý s druhým pravým, a tak ďalej, ako na obrázku pre n=5:
Hĺbka nejakej studne v ľavej polovici je potom tá, ktorú sme dostali v pokuse začínajúcom tou studňou, ale nie v tom, ktorý začína o jednu studňu vpravo; pre studne v pravej polovici je to to isté, ale symetricky opačne: hĺbka nejakej studne je tá, ktorá je v pokuse končiacom tou studňou, ale nie v pokuse o jednu studňu vľavo. Môžeme to vidieť na obrázku:

Týmto spôsobom teda vieme zistiť všetky hĺbky, a keď ich spočítame, zistíme, že ich je naozaj práve \left\lceil\left(n+1\right):2\right\rceil.
Zhrnutie
Tak to bol dosť dlhý vzorák :) ale povedali sme tam veľa vecí, ktoré nakoniec neboli priamo dôležité pre riešenie. Teraz si teda zhrňme, čo boli tie veci, ktoré sme nakoniec využili. Riešenie, ktoré nám vy odovzdáte, by malo vyzerať ako nejaké takéto zhrnutie. Tak poďme na to:
Všetky hĺbky vieme zistiť na N=\left\lceil\left(n+1\right):2\right\rceil pokusov.
Dolný odhad: Nech predel je miesto medzi dvoma studňami alebo za studňou na kraji radu. Každý pokus teda tvoria studne medzi dvoma predelmi. Ak existuje predel, v ktorom nezačína ani nekončí žiadny úsek, potom všetky pokusy obsahujú buď obe studne vedľa tohto predelu, alebo ani jednu, a tak hĺbky týchto studní nevieme rozlíšiť. V každom predeli teda musí mať krajný bod nejaký pokus. Keďže predelov je n + 1 a každý pokus má dva krajné body, pokusov musí byť aspoň N.
Konštrukcia: Očíslujme si studne 1 až n. Pre každé k od 1 po N urobíme pokus, v ktorom hodíme pražce do studní k, k+1, \ldots, k+\left\lceil n : 2 \right\rceil-1. Ak chceme zistiť hĺbku studne číslo k, je to presne tá hĺbka, ktorú dostanme v pokusoch číslo k-\left\lceil n : 2 \right\rceil+1 až k a v žiadnom inom. Budeme chcieť zisťovať studňu najviac n, na ktorú potrebujeme pokusy s číslom najviac N, takže tieto pokusy nám určite budú stačiť.
Tak, a to je všetko. Vidíte, nakoniec to riešenie nie je také hrozné, aj keď nie je ľahké na to prísť :)


