Vzorové riešenia 3. kola
1. príklad
Začneme štvorcom vľavo hore, pretože súčet daných čísel v ňom je najväčší, a to 15. Jeho ľavé horné políčko si označíme x a políčko v strede celého plániku napríklad a . Ďalej označíme ostatné políčka v rohoch pomocou x - dopočítame koľko chýba k hodnote v ľavom hornom štvorci (15 + x):

Teraz keďže vieme, že súčet čísel ktoré je potrebné doplniť je 23, môžme urobiť nasledovnú rovnicu:
x+x+5+x+9+x+4+a=23\\ 4x+a=5
Z tejto rovnice vieme povedať, že x môže byť iba 1, pretože a musí byť prirodzené číslo.
Dosadíme za x a vyjde nasledujúce riešenie:

Komentár
Veľa z vás zabudlo ukázať prečo neexistuje viac možností ako tie, ktoré ste našli. Toto bol vačšinou dôvod prečo ste strácali body. Okrem toho ste niektorí našli aj možnosť s nulou vľavo hore, no tá sa nie vždy považuje za prirodzené číslo. Preto sme za (ne)nájdenie tejto možnosti body nestrhávali. Celé riešenie by vyzeralo takto:

2. príklad
Najjednoduchšiu vec, ktorú môžeme spraviť je začať si kresliť prvé Šálkove kroky. Z náčrtu sa javí, že cesta sa točí do špirály. Postupne obchádza stred zo všetkých štyroch strán, no dĺžky ciest sa stále zväčšujú, takže nie je prekvapivé že vzďaľuje od stredu. Konkrétne sa pozrime na to, kde sa bude nachádzať po každých 4 cestách (Teda po 4., 8. atď.). Po prvých štyroch sa ocitne o 2 kroky na juh a o 2 na západ oproti začiatku, a to isté sa stane aj po ďalších štyroch, z čoho si môžeme tipnúť že to tak pôjde aj ďalej. Ak sa nám to podarí dokázať, ľahko už vypočítame výsledok.
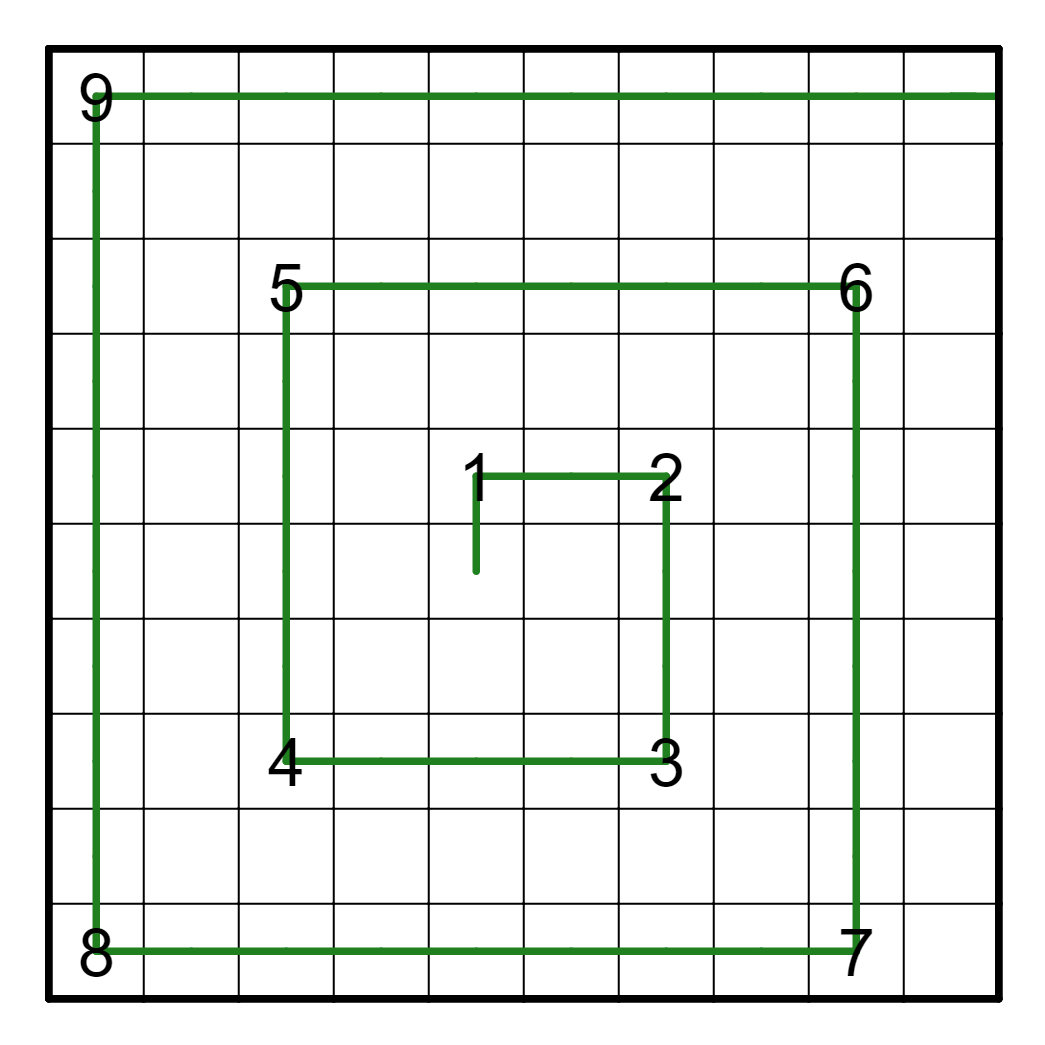
Poďme sa pokúsiť to vyvodiť z toho, čo platí pre každé takéto 4 cesty (začínajúce a končiace otočením na sever). To koľko krokov ktoré urobí Šálka na sever si označíme x. Šálka sa potom otočí na východ a posunie sa o jeden krok viac, teda urobí x+1 krokov. Pokračuje na juh a to x+2 krokmi a na západ x+3 krokmi.Šálka sa hýbe na navzájom opačné dvojice sever, juh a východ, západ. Zároveň keď sa hýbe niektorým z týchto smerov, neovplyvní tým, kde sa nachádza vzhľadom na smery z druhej dvojice. Keďže urobí x krokov na sever a x+2 krokov na juh, tak sa posunie o x-(x+2) krokov na sever, teda o -2 kroky (takže sa celkovo posunie o 2 na juh). Rovnako vypočítame posun na východ o x+1 mínus posun na západ o x+3 krokov, takže (x+1)-(x+3) = -2, takže sa posunie o 2 kroky na západ.
Prišli sme teda na to, že po každých štyroch cestách bude o 2 kroky viac južne a 2 kroky viac západne. V dokopy 80 cestách sa táto postupnosť 4 ciest zopakuje presne 80:4 = 20-krát. Dokopy sa teda posunie o 40 krokov na juh a rovnako o 40 krokov na západ. Z tohto miesta, kde skončil sa musí vrátiť naspäť rovnako veľa krokmi opačným smerom.
Odpoveď: Šálka teda musí urobiť 40 krokov na sever a 40 na východ.
Komentár
Skoro všetkým riešiteľom sa podarilo pomocou tipu na základe obrázka dostať ku správnemu výsledku. Viacerí z vás však nedokázali, že pravidlo o posunutí o 2 a 2 kroky bude s istotou platiť. To bol však veľmi dôležitý krok, bez ktorého zdôvodnenie riešenia nie je dostatočné, čo sa ukázalo aj na bodovaní príkladu. Za načrtnutie špirály a výpočet vedúci k výsledku sme udeľovali najviac 4 body, a zvyšné body sme udeľovali práve za overenie spomínaného pravidla.
3. príklad
Najprv potrebujeme zistiť, čo presne to Šálkovo tlačidlo s ľubovoľným číslom urobí. Operácie, ktoré kalkulačka robí, môžeme napísať aj ako výraz: ((n+4):4-4)\cdot4, kde n je ľubovoľné číslo, ktoré Šálka zadá do kalkulačky. Tento výraz nám, ale nič moc nepovie, takže ho musíme ešte upraviť:
((n+4):4-4)\cdot4=(\frac{n}{4}+\frac{4}{4}-4)\cdot4=(\frac{n}{4}+1-4)\cdot4=(\frac{n}{4}-3)\cdot4=n-12
Po upravení si môžeme všimnúť, že tlačidlo na Šálkovej kalkulačke zadané číslo zmenší o 12.
Keďže vieme, že zapísané čísla boli výsledky opakovaného stláčania tohoto tlačidla. Ak teda prvé číslo, ktoré zadal do kalkulačky je a, tak kalkulačka vypísala číslo a-12. Toto číslo po ďalšom slačení kalkulačka zmení na a-24. Potom, čo tlačidlo stlačíme tretí krát, kalkulačka číslo opäť zmenší o dvanásť, teda posledný výsledok bude a-36.
Zo zadanie vieme, že súčet všetkých štyroch čísel, ktoré si Šálka napísal je 80. Keďže sme si tieto štyri čísla už vyjadrili od pôvodného, môžeme tento vzťah zapísať pomocou rovnice: a+(a-12)+(a-24)+(a-36)=80.
Túto rovnicu si následne upravíme:
a+a-12+a-24+a-36=80
4a-72=80
4a=152
a=38
Takže číslo, ktoré si Šálka zapísal na papier ako prvé bolo 38. Ostatné čísla máme vyjadrené pomocou výrazov a-12, a-24 a a-36. Keď si do týchto výrazov dosadíme a=38, dostaneme zvyšné tri čísla − konkrétne 26, 14 a 2.
Odpoveď: Šálka si na papier napísal čísla 38,\, 26,\,14, \,2 v tomto poradí.
Komentár
Väčšina z vás výborne zvládla popísať obe časti riešenia − aj to, prečo kalkulačka znižuje číslo o 12, aj to, ako z toho vyplýva riešenie. Pri ostatných bol najväčší zádrheľ asi na dôkaze toho, čo tlačidlo na kalkulačke robí. Keďže tlačidlo vykonáva niekoľko operácií za sebou, nie je úplne triviálne, čo robí, a teda to treba poriadne vysvetliť prečo a ako sa na to dá dojsť.
4. príklad
Poďme sa pozrieť na to, čo sa stane keď ku škôlke (jej najspodnejšia časť je v obrázku zaznačená sivou) pridáme ďalší jeden rad štvorčekov.
Z obrázku teraz vidíme, že:
- Ak škôlka končila jedným štvorčekom, tak pridanie jedného štvorčeka pridalo 3 \, \text{dm} čiary.
- Ak sa škôlka končila jedným štvorčekom, tak pridanie dvoch štvorčekov pridalo 6 \, \text{dm} čiary.
- Ak sa škôlka končila dvomi štvorčekami, tak pridanie jedného štvorčeka pridalo 3 \, \text{dm} čiary.
- Ak sa škôlka končila dvomi štvorčekmi, tak pridanie dvoch štvorčekov pridalo 5 \, \text{dm} čiary.
Naríklad počet čiar v škôlke zo zadania vieme vypočítať ako súčet tvaru: 7 \, \text{dm} + 3 \, \text{dm}+3 \, \text{dm}+6 \, \text{dm}+3 \, \text{dm} = 22 \, \text{dm}.
Poďme teraz nájsť všetky možné šúčty do 26, ak súčet začína so 4. Zvyšok súčtu musí dať 22, teda v súčte musí byť 5 práve dvakrát. To preto, lebo 3, 6 sú násobky 3 a teda z nich vieme poskladať len medzi súčty 0,3,6,9,12,15,18,21,24,\dots a spomedzi týchto možných medzi súčtov iba pridanie +5+5 k 12 dá vo výsledku 22. 12 vieme poskladať ako 3+3+3+3, 3+3+6, 6+6. Máme teda tri možné skupiny čísel, z ktorých teoreticky vieme poskladať škôlku a majú súčet 26:
- 4,5,5,3,3,3,3 - z týchto čísel neposkladáme súčet nezodpovedajúci žiadnej škôlke, lebo 5 čiar nakreslíme iba ak dáme dvojicu štvorčekov za dvojicu štvorčekov.
- 4,5,5,3,3,6 - Máme iba jednu 6, teda obe 5 musia byť v súčte priamo za ňou. Z toho vieme poskladať tieto súčty ktoré zodpovedajú platným škôlkam:
- 4+6+5+5+3+3
- 4+3+6+5+5+3
- 4+3+3+6+5+5
- 4,5,5,6,6 - tu je problém, že máme dve 6 ale iba jednu 4 za ktorú ich vieme dokresliť, teda z týchto súčtov nejde poskladať súčet zodpovedajúci platnej škôlke.
Druhým variantom je, že hľadáme všetky možné šúčty do 26 ktoré začínajú 7. Zvyšok súčtu musí dať 19, teda v súčte musí byť 5 práve dvakrát z podobného dôvodu ako predtým, teda že 19 vieme poskladať iba ako 9+5+5 ako násobok 3 plus nejaký počet 5. 9 vieme poskladať ako 3+3+3 alebo 3+6. Máme teda dve možné skupiny čísel, z ktorých teoreticky vieme poskladať škôlku a majú súčet 26:
- Z čísel 7,5,5,3,3,3 vieme poskladať súčet pre platnú škôlku. Všimneme si, že 5 vieme nakresliť iba za 7 alebo 5, teda musia byť hneď na začiatku a súčet zodpovedajúci škôlke vyzerá ako:
- 7+5+5+3+3+3
- 7,5,5,3,6 - hlavná je pozícia 3. Hneď po nej musím totiž nakresliť 6. Vieme teda meniť iba pozície 3,5 z čoho jediné súčty zodpovedajúce skutočným škôlkam sú:
- 7+3+6+5+5
- 7+5+3+6+5
- 7+5+5+3+6
Odpoveď: Anka mohla nakresliť jednu zo 7 rôznych škôlok, ktoré majú 26 čiar.
Komentár
Väčsina z vás išla na príklad nejakou formou vypisovania možností, ako mohla škôlka vyzerať. Netreba však zabudať, že aj keď skúšate, tak je potrebné zdôvodniť, že ste skúsili všetky rozumné možnosti. Videli sme však, že ste sa pri riešení snažili, tak nech vám to vydrží aj po vianociach :D.
5. príklad
Ako prvé sa pozrieme na to ako sa nám menia súčty a súčiny jednotlivých cifier po zakódovaní:
| Pôvodná cifra | Nový súčet | Zmena súčtu | Nový súčin | Zmena súčinu | |
|---|---|---|---|---|---|
| 0 | 0 | 0 | 0 | celkový súčin bude 0 | |
| 1 | 2 | +1 | 1 | \cdot 1 | |
| 2 | 3 | +1 | 2 | \cdot 1 | |
| 3 | 4 | +1 | 3 | \cdot 1 | |
| 4 | 3 | -1 | 2 | \cdot \frac{1}{2} | |
| 5 | 4 | -1 | 4 | \cdot \frac{4}{5} | |
| 6 | 5 | -1 | 6 | \cdot 1 | |
| 7 | 4 | -3 | 3 | \cdot \frac{3}{7} | |
| 8 | 5 | -3 | 6 | \cdot \frac{3}{4} | |
| 9 | 6 | -3 | 9 | \cdot 1 |
Môžeme si všimnúť že súčet sa nám mení iba o +1; -1; -3 a pri nule o 0.
Tiež si môžeme všimnúť že súčin nám vždy zostáva rovnaký alebo sa znižuje, z čoho nám vyplýva že cifry ktorým sa znižuje súčin môžeme použiť iba ak použijeme aj nulu kedže nevieme nijako zvýšiť naspäť ciferný súčet.
Vieme teda rozlíšiť 2 možnosti, číslo obsahuje 0 a číslo neobsahuje 0.
Pozrieme sa najprv na možnosť že číslo obsahuje cifru 0, potom nás ciferný súčin nezaujíma kedže bude vždy 0. Môžeme si všimnúť že nemôžeme použiť cifru, ktorá sa zmení o -3 lebo nevieme dostať +3 iba dvoma ciframi. To znamená že môžeme použiť iba cifry, ktorým sa mení súčet o 0; +1 alebo -1. Teraz si môžeme všimnúť že súčet zvyšných troch z týchto čísel (môžu sa opakovať) sa bude rovnať 0 len ak budeme mať čísla -1; +1 a 0 alebo keď budem mať tri čísla 0. Druhú možnosť nevieme spraviť lebo štvorciferné číslo sa nemôže skladať zo štyroch núl. Takže sa pozrieme na to ako spraviť prvú možnosť:
- 0 viem dostať iba z cifry 0,
- +1 viem dostať iba z cifier 1; 2 a 3,
- -1 viem dostať iba z cifier 4; 5 a 6.
Teraz už len vyrátame počet štvorciferných čísiel ktoré viem vytvoriť z týchto cifier. Vieme že 0 nemôže byť na prvej pozícii takže tam musí byť jedno z čísel +1 a -1. Druhé z týchto čísel môže byť teda na jednej z troch pozícií (môže byť na 2.; 3. alebo 4.). To znamená že máme 3 rôzne zoradenia ak je na začiatku +1 a 3 rôzne zoradenia ak je na začiatku -1. Teraz si môžeme všimnúť že čísla +1 a -1 vyberáme nezávysle od seba a na každé máme 3 možnosti. To znamená že dokopy máme 3 \cdot 3 \cdot 3+3 \cdot 3 \cdot 3=54 možností vytvoriť štvorciferné číslo tak, že obsahuje nulu.
Teraz sa pozrieme na možnosť že číslo neobsahuje nulu. Potom nemôžeme použiť čísla 4; 5; 7 a 8 kedže tie znižujú ciferný súčin, ktorý nevieme nijak zvýšiť. Pozrieme sa teraz na to, akými kombináciami vieme získať rovnaký súčet.
Ak použijeme -3 tak +3 vieme získať iba použitím troch +1. Pozrieme sa na to, koľko takých štvorciferných čísel existuje:
- -3 vieme dostať iba z cifry 9,
- +1 vieme dostať iba z cifier 1; 2 a 3.
Cifra 3 môže byť na štyroch miestach a na zvyšných môžeme mať hociktorú z cifier 1; 2; 3. To znamená že máme 4 \cdot 3 \cdot 3\cdot 3=108 možností vytvoriť štvorciferné číslo obsahujúce cifru 9.
Ak použijeme -1 tak musíme použiť ešte jednu -1 a dve +1 (lebo 0 nemôžeme použiť, to sme zarátali pri možnostiach s nulami). Pozrieme sa teda na to, koľko je takýchto čísel:
- -1 vieme dostať iba z cifrier 4; 5 a 6,
- +1 vieme dostať iba z cifier 1; 2 a 3.
Čísla -1 môžu byť iba číslo 6. Prvú šestku môžeme mať na štyroch pozíciách a druhú na zvyšných troch pričom sa vedia vymeniť takže máme \frac{4 \cdot 3}{2} =6 možností rozmiestnenia čísel 6. Teraz nám zostali dve čísla +1 ktoré môžu byť hociktoré z 1; 2 a 3 takže máme dokopy 6 \cdot 3 \cdot 3=54 možností vytvoriť štvorciferné číslo obsahujúce dve cifry 6.
Ak by sme použili iba čísla +1 tak nevieme dostať súčet 0 a teda nebudeme mať číslo ktoré bude mať rovnaký ciferný súčet.
Dokopy máme teda 54+108+54=216 štvorciferných čísel ktoré majú pred aj po zakódovaní rovnaký ciferný súčet aj súčin.
Odpoveď:
Existuje 216 štvorciferných čísel ktoré majú po zakódovaní rovnaký ciferný súčet aj súčin.
Komentár
- Treba si veľmi dávať pozor pri dokazovaní. Ak zistíte, že kombinácie skupín čísel \left\lbrace +1; +1; -1; -1\right\rbrace; \left\lbrace +1; -1; 0; 0\right\rbrace a \left\lbrace +3; -1; -1; -1\right\rbrace dávajú riešenia tak je to bomba, no ostáva ešte kopa práce. Treba ukázať, že sú naozaj všetky a to je často zapeklitý problém, ktorý netreba podceniť a určite budete odmenení bodmi.
- Ďalej ste sa občas vcelku trápili s rátaním kombinácií, keď už ste mali zistené, čo vlastne máte rátať. Určite sa pri riešení dá vypisovať, no často to nie je sranda, hlavne keď sa niekde v strede náhodou zašmodrcháte. Ak ste sa teda už stretli s faktoriálmi, tak vrelo odporúčame sa s nimi skamarátiť. Ak nie tak sa tešte na sústredenie.
- Nakoniec ste si niektorí povedali, že nemôžeme použiť tie čísla, ktorým sa mení cif. súčin ale neuvedomili ste si, že ak použijeme cifru 0 tak nás ciferný súčin nezaujíma. Iní zase naopak usúdili, že musíme použiť 0, aby sme "napravili" tieto čísla a neuvedomili si že sa dajú vytvoriť aj čísla, v ktorých nepoužijeme 0 a nezmení sa im súčin. To je samozrejme nepríjemnosť, no nabudúce to určite vyjde lepšie.
Bodovanie
Tento príklad sme bodovali nasledovným spôsobom:
- 1 bod ste mohli získať, ak ste si napísali tabuľku alebo inak pozorovali rozdiely súčtov a súčinov.
- 3 body ste mohli získať za správne vypočítanie počtu riešení pre čísla obsahujúce cifru 0.
- 2 body ste mohli získať za správne vyrátanie počtu riešení pre čísla obsahujúce -3.
- Ďaľšie 2 body ste mohli získať za správne vyrátanie počtu riešení pre čísla obsahujúce práve dve -1.
- A nakoniec po jednom bode ste mohli získať za ukázanie, že čísla 4; 5; 7 a 8 nemôžeme použiť ak v čísle nie je cifra 0 a za správne dokázanie, že \left\lbrace +1; +1; -1; -1\right\rbrace; \left\lbrace +1; -1; 0; 0\right\rbrace a \left\lbrace +3; -1; -1; -1\right\rbrace sú jediné kombinácie zmien súčtov ktoré vyhovujú zadaniu.
6. príklad
Uvedomme si, že zaokrúhlením čísla n na najbližší násobok 7 sa určite nezmení o viac ako o 3. Prečo? Označme si tento najbližší násobok 7 písmenom s. Vieme aj, že s-7 a s+7 budú násobky 7, pretože každé siedme celé číslo je násobkom 7. Teraz ukážme, prečo n nemôže byť od s vzdialenejšie ako o 3:
Pokiaľ n = s-4 alebo menej, tak s prestane byť najbližším násobkom 7, pretože s-7 je k n bližšie. Rovnako keby n = s+4 alebo viac, tak s+7 je k n bližšie ako s.
Rovnako platí, že zaokrúhlením n na najbližší násobok 5, ktorý označíme p, sa určite nezmení o viac ako 2, pretože keby n = p+3 alebo viac tak by bolo p+5 bližšie, a keby n = p-3 alebo menej tak by bolo bližšie p-5.
Pozrime sa teraz na prvú rovnicu:
(4x)_5 + 7y = 15
Spravme menšiu úpravu odrátaním prvého sčítanca od oboch strán:
7y = 15 - (4x)_5
Vidíme, že oba sčítance na pravej strane sú násobky 5, teda celá pravá strana je násobkom 5. Z toho logicky vyplýva, že ľavá strana, ktorá je rovná 7y, je tiež násobkom 5. 7y je zjavne aj násobkom 7, teda platí, že 7y je násobkom 5 \cdot 7 = 35. To znamená, že 7y vieme napísať ako 35k, kde k je nejaké celé číslo. Upravme rovnicu vydelením oboch strán 7 a dostaneme 5k = y. Takže vidíme, že y je nejaký celočíselný násobok 5.
Okrem toho si z tohto vieme odvodiť, že aj 2y je násobok 5, a teda (2y)_5 musí byť 2y, pretože žiaden iný násobok 5 nebude bližšie k 2y ako ono samotné.
Prejdime na druhú rovnicu:
(2y)_5 - (3y)_7 = 74
Ako sme pred chvíľou ukázali, vieme si ju upraviť nasledovne:
2y - (3y)_7 = 74
Vieme už, že menšiteľ (3y)_7 sa musí od 3y líšiť o najviac 3. To znamená, že celá ľavá strana rovnice sa od 2y-3y = -y môže líšiť najviac o 3, a teda aj pravá strana 74 sa musí od -y líšiť najviac o 3. Inak povedané, -y musí byť nejaké číslo od 74-3 = 71 do 74+3 = 77. Obrátime znamienko, a zisťujeme, že y musí byť číslo od -77 do -71. Už ale vieme, že y je násobkom 5, a jediné číslo v tomto rozsahu deliteľné 5 je -75. Teda vieme, že musí platiť, že y = -75.
Dosaďme túto hodnotu do prvej rovnice:
(4x)_5 + 7 \cdot (-75) = 15
(4x)_5 - 525 = 15
(4x)_5 = 540
4x = 540
x = 135
Podarilo sa nám ukázať, že hodnoty x a y môžu byť iba 135 a -75. Stále je však možné, že toto nie je správne riešenie, ak žiadne neexistuje. Preto spravme skúšku správnosti:
(4x)_5 + 7y = 15
(540)_5 - 525 = 15
540 - 525 = 15
15 = 15
(2y)_5 - (3y)_7 = 74
(-150)_5 - (-225)_7 = 74
-150 - (-224) = 74
-150 + 224 = 74
74 = 74
Teraz vidíme, že naše riešenie rovnici naozaj vyhovuje.
Odpoveď: x = 135; y = -75
Komentár
Najviac chýb spočívalo v tom, že riešenia predpokladali, že keď hľadáme číslo, ktorého najbližší násobok m je mk, tak jedinou možnosťou je najbližšie číslo k mk. Napríklad keď hľadáme násobok 3, pre ktorý platí, že jeho najbližší násobok 7 je 28, tak to nemusí znamenať, že hľadaným násobkom je 27. Aj 30 je totiž zo všetkých násobkov 7 najbližšie k 28, napriek tomu, že je od 28 ďalej ako 27.
7. príklad
Označíme si príchute pudingov A, B, C, D, E a F. Pozrime sa teraz na možnosť, keď je počet porotcov deliteľný 5. Teraz môžeme prvým piatim dať postupne príchute ABCDE a toto zopakovať pre každú ďalšiu päticu. V tejto postupnosti pre ľubovoľný puding platí, že nasledujúca aj predchádzajúca štvorica pudingov obsahuje rovnaké pudingy v rovnakom poradí a neobsahuje zvolenú príchuť pudingu.
Pozrime sa teraz na prípad, kde je počet porotcov deliteľný 6. Prvým 6 porotcom dáme postupne príchute ABCDEF a tieto príchute zopakujeme pre každú ďalšiu šesticu. Táto postupnosť vyhovuje zadaniu z rovnakého dôvodu ako pri možnosti s počtom porotcov deliteľnom 5.
Povedzme, že sa počet porotcov dá rozdeliť na 2 úseky, kde dĺžka prvého je deliteľná 5 a dĺžka druhého je deliteľná 6. Teraz sa na tieto úseky môžeme pozrieť ako na 2 rôzne situácie a rozdeliť príchute tak, ako sme si ukázali vyššie. Jediná možnosť, kde sa mohlo toto rozdelenie "pokaziť" je pri porotcoch, ktorí sú na hranici medzi jednotlivými úsekmi. Tam príchute vyzerajú nasledovne ABCDE ABCDEF a ABCDEF ABCDE. Tuto sa pravidlo zo zadania zjavne neporušilo, teda ľubovoľné m, ktoré sa dá zapísať ako súčet 5x a 6y vyhovuje zadaniu.
Pozrime sa, ktoré všetky m sa takto dajú vyskladať. Vyskladať sa dá napríklad m = 20 = 5 \cdot 4, m =21 = 5 \cdot 3 + 6, m = 22 = 5 \cdot 2 + 6 \cdot 2, m = 23 = 5 + 6 \cdot 3 a m = 24 = 6 \cdot 4. Keďže dokážeme vyskladať 5 po sebe idúcich čísel, tak dokážeme vyskladať aj ľubovoľné číslo väčšie ako 24 a to tak, že k jednému z čísel 20 až 24 pripočítame násobok 5. Teda obslúžiť sa dá určite ľubovoľný počet porotcov m, kde m \geq 20. Ostatné m sa dajú vyskladať všetky, okrem 7, 8, 9, 13, 14 a 19. Poďme teda dokázať, že pre tieto počty porotcov sa príchuťe pudingov nedajú rozdeliť podľa zadania.
Keďže príchutí je 6, tak pre m = 7, m = 8 a m = 9 platí, že aspoň 1 príchuť sa bude musieť vyskytovať 2-krát, lebo ak by sa vyskytovala len raz, rozhodcovia by vedeli dostať len 6 pudingov. No ale na to, aby sme vedeli rozhodcom dať 2 pudingy s rovnakou príchuťou, potrebujeme aspoň 2 + 2 \cdot 4 = 10 porotcov, lebo medzi 2 pudingami s rovnakou príchuťou musia byť aspoň 4 iné pudingy. Teda počty porotcov 7, 8 a 9 nevyhovujú zadaniu.
Pre m = 13 a m = 14 sa musí nejaká príchuť vyskytovať medzi pudingami aspoň 3-krát, keby sa každá príchuť vyskytovala 2-krát mali by sme dokopy len 2 \cdot 6 = 12 pudingov. Na to, aby sme rozhodcom vedeli dať aspoň 3 pudingy s rovnakou príchuťou treba aspoň 3 + 3 \cdot 4 = 15 porotcov, lebo medzi 2 pudingami s rovnakou príchuťou musia byť aspoň 4 iné pudingy. Teda počty porotcov 13 a 14 nevyhovujú zadaniu.
Pre m = 19 sa musí nejaká príchuť vyskytovať aspoň 4-krát, lebo keby sa každá príchuť vyskytovala len 3-krát, tak by sme vedeli obslúžiť len 18 porotcov. Na to, aby sme rozhodcom vedeli dať aspoň 4 pudingy s rovnakou príchuťou treba aspoň 4 + 4 \cdot 4 = 20 porotcov, lebo medzi 2 pudingami s rovnakou príchuťou musia byť aspoň 4 iné pudingy. Teda porotcov nemôže byť ani 19.
Odpoveď: Rozdať pudingy Jerguš dokáže pre všetky počty rozhodcov m (väčšie ako 4), okrem 7, 8, 9, 13, 14 a 19.
8. príklad
Zamyslime sa najprv nad vpísanou kružnicou. Prvá vec, ktorá nám napadne, je, že jej stred I leží na priesečníku osí vnútorných uhlov trojuholníka. To napríklad znamená, že |\measuredangle ECI| = |\measuredangle DCI|. Ďalej máme v zadaní jej body dotyku, pričom najmä D a E sa spomínajú opakovane. Tu využijeme fakt o uhle medzi dotyčnicou a úsečkou spájajúcou bod dotyku so stredom. Takýto uhol je vždy pravý. Dostávame |\measuredangle CEI| = |\measuredangle CDI| = 90°.
Trojuholníky CEI,\, CDI majú rovnaké dva uhly. Pre zvyšné teda platí
|\measuredangle CIE| = 180° - |\measuredangle ECI| - |\measuredangle CEI| = 180° - |\measuredangle DCI| - |\measuredangle CDI| = |\measuredangle CID|,
čiže sa aj tie rovnajú. Teraz si môžeme všimnúť, že úsečka CI je pre oba trojuholníky spoločná. Potom sú trojuholníky CEI a CDI zhodné podľa vety USU.
V zadaní sa pýtame na bod G, o ktorom toho nevieme veľa. Vieme však niečo o priamke p, na ktorej bod G leží. Tá je rovnobežná s úsečkou DE. Vráťme sa späť k práve dokázanej zhodnosti trojuholníkov. Podľa nej majú CEI a CDI rovnaké strany, takže |CE| = |CD|. Trojuholník CDE je rovnoramenný so základňou DE, čo sa nám náramne hodí. Taktiež uhly \measuredangle CDE a \measuredangle CED sú rovnaké.
Naspäť k našej rovnobežke p. Uhly \measuredangle CED a \measuredangle CGB sú súhlasné a teda rovnako veľké. To isté platí aj pre uhly \measuredangle CDE a \measuredangle CBG. Trojuholník CGB má teda uhly pri základni GB rovnako veľké, takže je to rovnoramenný trojuholník.
Pozrime sa teraz na to, čo potrebujeme zistiť. Zaujíma nás veľkosť uhla \measuredangle EGI, ak poznáme \measuredangle ABC. Skvelé uvedomenie je, že ak poznáme veľkosť \measuredangle ABC, poznáme aj veľkosť \measuredangle DBI. Bod I leží na osiach vnútorných uhlov, takže tento uhol bude polovicou \measuredangle ABC. Stačí nám teda zistiť vzťah \measuredangle EGI a \measuredangle DBI.
Prejdime od uhlov k trojuholníkom. Konkrétne EGI a DBI. Mohli by byť zhodné? Už vieme, že uhly \measuredangle GEI a \measuredangle BDI sú oba pravé. Vieme tiež, že úsečky DI a EI sú polomery vpísanej kružnice, čiže majú rovnakú dĺžku. Na zhodnosť by nám stačila už len rovnosť |EG| = |DB|. Skúsime si vyjadriť ľavú stranu podľa toho, čo už vieme:
|EG| = |CG| - |CE| = |CB| - |CD| = |DB|.
Prostredná rovnosť platí vďaka |CG| = |CB| a |CE| = |CD| odvodeným vyššie. Trojuholníky EGI a DBI sú teda zhodné podľa vety SUS. Majú teda rovnaké uhly a špeciálne platí |\measuredangle EGI| = |\measuredangle DBI| = \frac{1}{2} \cdot |\measuredangle ABC|.
Odpoveď: Veľkosť uhla \measuredangle EGI je \dfrac{1}{2} \cdot |\measuredangle ABC|.
Komentár
Ako najťažší krok sa ukázalo odvodenie zhodnosti trojuholníkov CDI a CEI. Pritom sa dal úplne obísť a vypočítať priamo uhly \measuredangle CDE a \measuredangle CED pomocou pravých uhlov spomínaných vyššie a rovnoramennosti trojuholníka DIE. Najčastejšou chybou bolo využitie len jednej rovnosti uhlov zo spomínaných na začiatku vzoráku. K tomu sa okrem spoločnej CI pridali polomery DI a EI a použila sa veta SSU. Takáto veta o zhodnosti trojuholníkov však neexistuje.
Na obrázku máme trojuholníky ABC a A'BC. Tie majú dve rovnako dlhé strany - A,A' ležia na kružnici so stredom C a BC je spoločná. Majú tiež spoločný uhol |\measuredangle ABC| = |\measuredangle A'BC|. Zjavne však nie sú zhodné. Dve strany a uhol na dôkaz zhodnosti stačia len, ak je rovnaký uhol medzi danými dvoma stranami (SUS).
9. príklad
Zadanie sa môže na prvý pohľad zdať dlhé a zložité, no po chvýli skúšania je možné si všimnúť opakújuci sa vzor, ktorý je kľúčom k riešeniu. Poďme to teda rozlúštiť.
Nazvime krok o jedna dolu a o dve doprava ako obyčajný. Všimnime si, že obyčajným krokom stúpim z políčka A na políčko B, kde už sú piškóty, tak pôvodne sme tieto piškóty museli umiestniť iným než obyčajným spôsobom. Totiž, ak by sme ich pôvodne na B umiestnili obyčajným spôsobom znamenalo by to, že tento krok začínal v A. To by však znamenalo, že v A už tiež musia byť piškóty a teda by sme z neho nemohli spraviť obyčajný krok.
Po n obyčajných ťahoch z políčka X sa opäť dostaneme na políčko X keďže sa spolu pohneme o 2n vpravo a o n nadol. Prejdeme teda cez každý riadok nakoľko n je nepárne a teda je nesúdeliteľné s 2. Na n-tý ťah skočíme na riadok, na ktorom je X. Taktiež skočíme na stĺpec, kde je X, lebo sa pohneme o n nadol. Čiže na každý stĺpec skočím práve raz, nakoľko po vyskočení z tabuľky sa vrátime naspäť. Keď teda začneme v ľavom hornom rohu, po n ťahoch skočíme na toto isté políčko. Po ceste neskočíme na žiadne piškóty a to preto, lebo žiadne iné políčko nebude mať piškóty vložené inak ako po obyčajnom ťahu.
Následne spravíme neobyčajný ťah o dve vľavo a jedno dole a skončíme na políčku Y. Teraz je jediné políčko s piškótami na ktoré môžeme skočiť Y, keďže na všetky ostatné zaplnené políčka sme sa už pohli obyčajným ťahom. Spravíme teda ďaľších n obyčajných ťahov a ocitneme sa na políčku Y. Opäť teda vykonáme neobyčajný ťah a tým začneme nový cyklus. Pod pojmom cyklus myslíme n po sebe idúcich obyčajných ťahov, ktoré začínajú aj končia na rovnakom poličku. Ako sme už vyššie ukázali takýto cyklus prechádza cez každý riadok aj každý stĺpec práve raz. Prvý cyklus začína v ľavom hornom rohu.
Už sme takéto cykly spravili dva a vždy keď sa po skončení cyklu pohneme, bude to začiatok nového, keďže potom urobíme n obyčajných krokov späť na toto políčko. Takýchto cyklov bude n, keďže v každom cykle uložím piškóty na n políčok a tých je celkovo n^2.
Začiatky cyklov sa hýbu vždy o jedno políčko dole a o dve doľava. Tým pádom bude jeden začiatok cyklu v každom riadku a v každom stĺpci. To preto, lebo 2 je nesúdeliteľné s n, keďže n je nepárne.
V k-tom cykle umiestnime postupne na políčko na začiatok cyklu (k-1) \cdot n +1 piškôt, na druhé políčko (k-1) \cdot n +2, na tretie (k-1) \cdot n +3 a tak ďalej. Až na n-té políčko cyklu umiestnime (k-1) \cdot n + n piškôt. Prvý cyklus začína na políčku vľavo hore. Počas jedného cyklu pridáme do každého riadku aj každého stĺpca (k-1) \cdot n piškôt a do každého z nich potom pridáme počet piškôt podľa toho koľkaté je dané políčko v cykle. Nás bude zaujímať práve tento zvyšok, keďže všetko ostatné je rovnaké pre každý riadok aj každý stĺpec.
Všimnime si, že každý riadok/stĺpec bude v jednom cykle prvý, v jednom cykle druhý, v jednom cykle tretí atď až v jednom cykle n-tý. Teda súčet zvyškov v každom riadku/stĺpci bude rovnaký. Preto aj súčet každého riadku/stĺpca bude rovnaký.
Komentár
Väčšina z vás si správne všimla ako sa správajú cykly no po väčšine ste nedokázali, že vrámci cyklu nenarazíme na žiadne políčko (okrem začiatočného políčka cyklu) kde už boli piškóty predtým.
10. príklad
Počet trojkových čísel vieme vypočítať ako počet čísel, ktoré obsahujú cifru 3 , plus počet čísel ktoré ju neobsahujú, ale sú deliteľné tromi.
Najskôr vypočítame počet takých čísel do 10^n , ktoré obsahujú cifru 3 . Najjednoduchšie to vieme urobiť tak, že od celkového počtu čísel odpočítame tie, ktoré trojku neobsahujú. Počet všetkých čísel je zjavne 10^n . Teraz sa pozrieme na tie z nich, ktoré neobsahujú cifru 3 . Na mieste každej cifry môže byť ľubovoľné číslo od 0 do 9 okrem trojky. To je 9 možností pre každú z cifier n -ciferného čísla, teda celkovo dostávame 9^n možností. Môžeme si rozmyslieť, že sú všetky naozaj rôzne. Týmto kombinovaním cifier vznikli aj čísla, ktoré sa začínajú na jednu alebo viac núl. Tie po odstránení núl na začiatku predstavujú všetky menej ako n -ciferné čísla. Okrem toho vznikne aj číslo 0 , ktoré nie je prirodzeným číslom od 1 do 10^n . Zároveň 10^n sme týmto spôsobom nedostali, aj keď neobsahuje cifru 3 . Jedno číslo sme teda zarátali aj keď sme nemali, jedno iné sme nezarátali, aj keď sme ho mali zarátať. Počet čísel od 1 do 10^n , ktoré neobsahujú cifru 3 je teda 9^n-1+1=9^n .
Čísel, ktoré obsahujú cifru 3 je 10^n-9^n .
Nuž a koľko je čísel, ktoré cifru 3 neobsahujú, ale sú deliteľné tromi? Tu si pomôžeme poznatkom, že číslo je deliteľné tromi práve vtedy, keď je jeho ciferný súčet deliteľný tromi. To dosť zjednodušuje úlohu a umožňuje to nepozerať sa na každú cifru zvlášť, ale urobiť menší trik.
Majme nejakú kombináciu pre prvých n-1 cifier, v ktorej nie je cifra 3 . Aká môže byť posledná cifra na to, aby bolo celé n -ciferné číslo deliteľné tromi a zároveň neobsahovalo trojku? Tu sú tri možnosti, ako \left(n-1\right) -ciferné číslo mohlo vyzerať.
- Zvyšok po delení súčtu prvých n-1 cifier trojkou je 1 . Číslo po pridaní poslednej cifry bude deliteľné tromi práve vtedy, keď bude zvyšok po delení poslednej cifry 2 . Zvyšky sa totiž sčítajú, 1+2=3 , čo dáva po delení tromi zvyšok 0 . Číslo bude teda deliteľné troma. Jednociferné čísla, ktoré dávajú po delení tromi zvyšok 2 sú tri, a to 2,\, 5,\, 8 .
- Zvyšok po delení súčtu prvých n-1 cifier je 2 . Keď pridáme poslednú cifru, číslo bude deliteľné tromi, ak sme pridali číslo, ktoré má po delení tromi zvyšok 1 . Tieto čísla sú tiež tri, a to 1,\,4,\,7 .
- Súčet prvých n-1 cifier je deliteľný tromi, teda dáva zvyšok 0 . Súčet aj s poslednou cifrou bude potom deliteľný troma vtedy, keď bude posledná cifra deliteľná tromi. Číslo 3 samotné nepoužívame, lebo hľadáme čísla deliteľné tromi, ktoré trojku neobsahujú. Zostali tak tri možnosti, a to 0,\,6,\,9 .
Ako vidíme, možnosti na doplnenie poslednej cifry sú vždy tri.
Počet kombinácií cifier na prvých n-1 miestach bez použitia trojky je 9^{n-1} . Použili sme na to rovnakú úvahu ako keď sme zisťovali na začiatku počet čísel do 10^n , ktoré neobsahujú trojku, len to robíme s o jedna menším počtom cifier. Tým dostávame 9^{n-1} \cdot 3 čísel. Ošetriť ešte musíme čísla 0 a 10^n . V počte 9^{n-1} \cdot 3 je zarátaná aj 0 , ktorá nie je číslom od 1 do 10^n . Číslo 10^n sme kombináciami cifier nemohli dostať, lebo sme sa pozerali na najviac n-ciferné čísla. Zároveň ale nejde o číslo deliteľné tromi, takže ho do počtu čísel, ktoré sú deliteľné tromi a neobsahujú trojku pripočítavať nejdeme. Po odpočítaní možnosti, kde vyšla 0 dostávame, že čísel, ktoré sú deliteľné tromi ale cifru 3 neobsahujú je 9^{n-1} \cdot 3 -1 .
Odpoveď: Počet trojkových čísel od 1 do 10^n je \left(10^n-9^n\right) + \left(9^{n-1} \cdot 3 -1\right) .
Komentár
Pomohlo nám, že číslo je deliteľné tromi práve vtedy, keď je jeho ciferný súčet deliteľný tromi. Platí dokonca aj silnejšie tvrdenie, číslo má po delení tromi rovnaký zvyšok ako jeho ciferný súčet. A keby to nestačilo, podobne to funguje aj pre deviatku, číslo má po delení deviatimi zvyšok rovnaký, ako má jeho ciferný súčet. V úlohách s deliteľnosťami a hľadaním rôznych čísel podľa podmienok sa tieto tvrdenia veľmi často dajú využiť, je dobré si ich pamätať.
Viacerí z vás použili v riešení takzvané sumy. Tie nepovažujeme za základné aritmetické operácie, strhávali sme za ne body.
Prémia 1
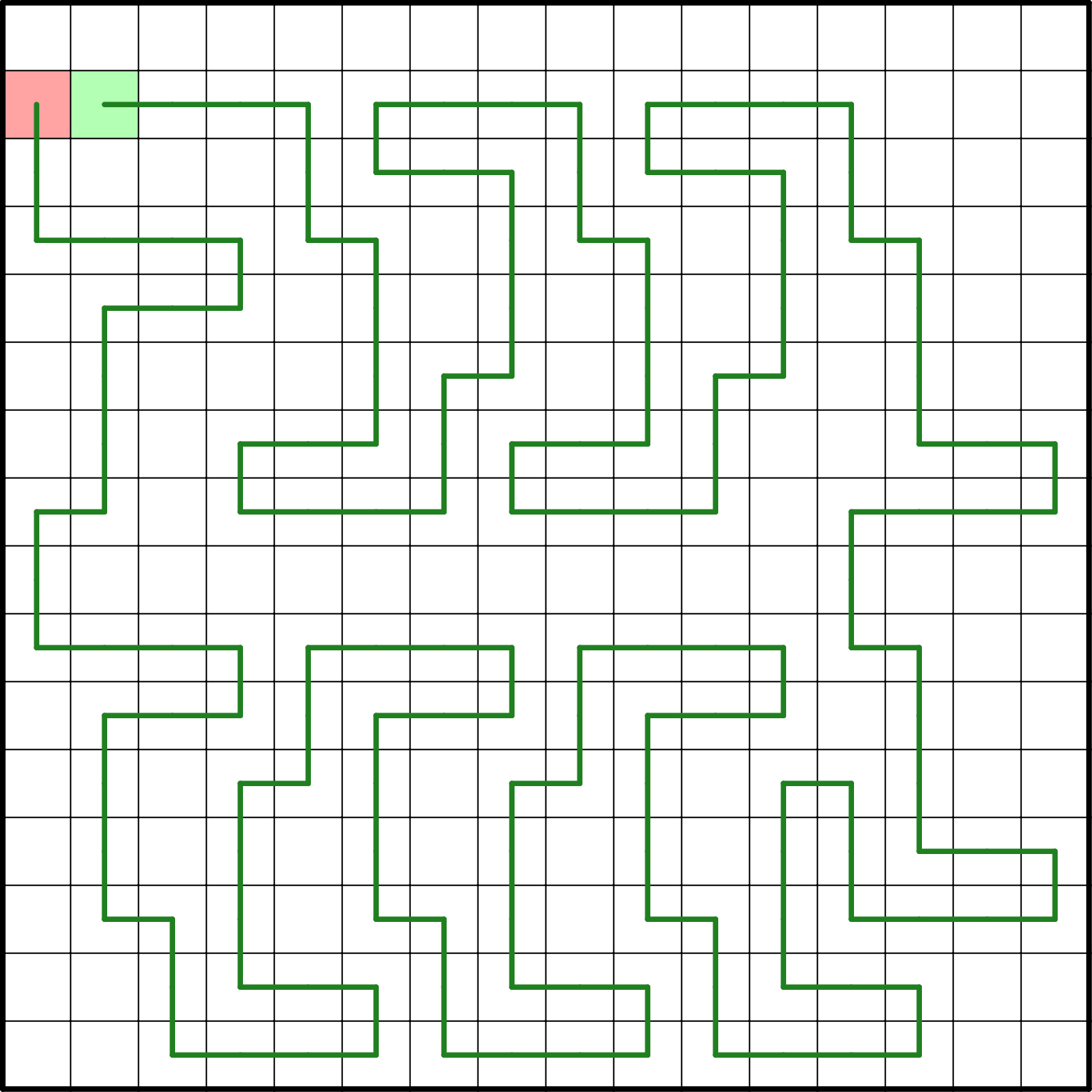
Odpoveď: Najdlhšia žížalka, akú sa vám podarilo nájsť, prechádzala cez 162 políčok. Takáto žížalka mohla vyzerať napríklad takto:
Komentár
Kľúčovým krokom pri dosiahnutí vysokého počtu prejdených políčok bolo všimnutie si kompaktného tvaru do ktoreho vieme uložiť 24 políčok žížalky. Aj v tomto riešení je použitý 6-krát, a obsahovali ho všetky riešenia. Je tak kompaktný, že sme mohli úplne zabudnúť na vrchný riadok, ktorý sme nepoužili. Viac sa oplatilo použiť dva rady týchto tvarov vysoké sedem, ako tabuľku vypĺňať od kraja iným spôsobom.
Bodovanie
Riešenia sme bodovali podľa počtu políčok ktoré prešla vaša žížalka nasledovne:
- 162 políčok - 8 bodov,
- 155 až 161 políčok - 7 bodov,
- 145 až 154 políčok - 6 bodov,
- 130 až 144 políčok - 5 bodov,
- 125 až 129 políčok - 4 body,
- 105 až 124 políčok - 3 body,
- 90 až 104 políčok - 2 body,
- 89 a menej políčok - 1 bod.




