Vzorové riešenia 3. kola
1. príklad
Označme si počet všetkých kamienkov okrem jedného ako x.
Počet v 1. krabici vypočítame tak, že x vydelíme 10, k čomu pridáme ešte tú jednotku, ktorú sme už na začiatku odpočítali.
\displaystyle \frac{x}{10} + 1 = y
Počet v 2. krabičke zistíme tak, že si zistíme koľko ich ostalo. Ostalo ešte \frac{9}{10}\cdot x, pretože sme odpočítali len jednu desatinu pri 1. krabičke. Z tohto zvyšku odpočítame 2, ktoré vložíme najprv a až to vydelíme 10. Nakoniec ešte pripočítame 2.
Keďže vieme, že vo všetkých krabiciach je rovnaký počet kameňov, tak si môžeme spraviť túto rovnicu:
\displaystyle \hspace{1.2cm} \frac{x}{10} + 1 = \frac{9x:10 - 2}{10} + 2 \hspace{0.6cm} /\cdot 10 \\[5pt] \hspace{1.2cm} x + 10 = \frac{9x}{10} - 2 + 20 \hspace{0.6cm} /-0{,}9x-10 \\[5pt] \hspace{1.2cm} 0{,}1x = 8 \hspace{0.6cm} /\cdot 10 \\[5pt] \hspace{1.2cm} x = 80
Celkový počet kamienkov bude o 1 väčší:
80 + 1 = 81
Počet kamienkov v jednej krabici:
80:10+1 = 9
Počet krabíc:
81:9 = 9
Odpoveď: Pred dverami bolo 81 kamienkov a dobrodruhovia ich ukladali do 9 skriniek.2. príklad
Keďže každý ihlan je zafarbený celý jednou farbou, tak každý ihlan určuje farbu jednej zo stien kocky (napr. ak je podstavný ihlan červený tak dolná stena bude tiež červená). Ak sa pozrieme na kocku, rovnaké farby nemôžu byť na stranách dotýkajúcich sa hranami, lebo by sa ihlany rovnakej farby navzájom dotýkali jednou z bočných stien. Každý ihlan sa týmito bočnými stenami teda dotýka ďalších 4 ihlanov (každá stena kocky sa hranou dotýka ďalších 4 stien) a jedným bodom sa dotýka ihlanu oproti, tie však podľa zadania môžu byť rovnakej farby. Rovnaká farba teda môže byť iba na stranách kocky oproti sebe.
To znamená, že nevieme použiť iba jednu farbu lebo by sme zafarbili nanajvýš dve steny. Takisto nevieme zafarbiť kocku ani dvomi farbami lebo by sme zafarbili najviac 2\cdot2=4 steny.
Najmenší počet farieb, koľkými môžeme zafarbiť kocku, je teda 3. Ak už si nejaké tri farby zvolíme, je iba jedna možnosť, ako nimi ofarbiť kocku. Prvou farbou ofarbíme ľubovoľné protiľahlé strany, povedzme hornú a dolnú. Druhou jednu zo zvyšných dvojíc, no je jedno ktorú, keďže jednoduchým otočením kocky podľa zvislej osi vieme dosiahnuť druhú možnosť. Na poslednú farbu nám už ostali voľné len dve strany, a teda nemáme na výber. No a tri farby vieme zvoliť štyrmi spôsobmi, vždy jednu zo 4 farieb nepoužijeme. Preto sú \mathit{4} možnosti ofarbenia kocky iba tromi farbami.
| Predná | Zadná | Pravá | Ľavá | Spodná | Horná | |
|---|---|---|---|---|---|---|
| 1. možnosť | červená | červená | zelená | zelená | oranžová | oranžová |
| 2. možnosť | červená | červená | zelená | zelená | fialová | fialová |
| 3. možnosť | červená | červená | oranžová | oranžová | fialová | fialová |
| 4. možnosť | zelená | zelená | oranžová | oranžová | fialová | fialová |
Teraz potrebujeme spočítať možnosti, kde použijeme všetky 4 farby. Musíme pritom však dodržať pravidlo, že rovnaké farby môžu byť iba oproti sebe. To vieme splniť jedine tak, že dvakrát použijeme farbu na dvojicu steny oproti sebe a na zvyšné dve steny dáme zvyšné \mathit{2} farby. Toto vieme dosiahnuť tak, že v našich trojfarebných riešeniach jednu zo stien prefarbíme na farbu, ktorú tam nepoužívame. Takto pre každe zo štyroch riešení dostaneme 3 nové, keďže nám nezáleží na tom, ktorú z dvoch protiľahlých stien prefarbíme. Je to tak preto, lebo druhú možnosť vieme jednoducho dosiahnuť prevrátením kocky. Naše ofarbenia budú teda takéto (na pomenovaní stien resp. otočení kocky nezáleží):
| 1. možnosť | Predná | Zadná | Pravá | Ľavá | Spodná | Horná |
|---|---|---|---|---|---|---|
| A možnosť | červená | červená | zelená | zelená | oranžová | fialová |
| B možnosť | červená | červená | zelená | fialová | oranžová | oranžová |
| C možnosť | červená | fialová | zelená | zelená | oranžová | oranžová |
| 2. možnosť | Predná | Zadná | Pravá | Ľavá | Spodná | Horná |
|---|---|---|---|---|---|---|
| A možnosť | červená | červená | zelená | zelená | fialová | oranžová |
| B možnosť | červená | červená | zelená | oranžová | fialová | fialová |
| C možnosť | červená | oranžová | zelená | zelená | fialová | fialová |
| 3. možnosť | Predná | Zadná | Pravá | Ľavá | Spodná | Horná |
|---|---|---|---|---|---|---|
| A možnosť | červená | červená | oranžová | oranžová | fialová | zelená |
| B možnosť | červená | červená | oranžová | zelená | fialová | fialová |
| C možnosť | červená | zelená | zelená | zelená | oranžová | oranžová |
| 4. možnosť | Predná | Zadná | Pravá | Ľavá | Spodná | Horná |
|---|---|---|---|---|---|---|
| A možnosť | zelená | zelená | oranžová | oranžová | fialová | červená |
| B možnosť | zelená | zelená | oranžová | červená | fialová | fialová |
| C možnosť | zelená | červená | oranžová | oranžová | fialová | fialová |
Nakoniec si ale ešte treba všimnúť, že niektorými prefarbeniami môžem dostať rovnaké ofarbenie kocky. Konkrétne, keď máme napríklad kocku, ktorá má zeleno-fialovú dvojicu stien oproti sebe, dostať sme ju mohli, buď prefarbením jednej zelenej steny na fialovú, alebo jednej fialovej na zelenú. Rovnako bude platiť pre každé ofarbenie štyrmi farbami to, že ho vieme dostať dvoma spôsobmi. Preto z dvanástich ofarbení v tabuľke nájdeme iba 6 rôznych.
Kocka teda dokopy teda dokopy môže mať 4+6~{=}\mathit{10} ofarbení zvonku.
3. príklad
Štvorciferných čísel je veľa (9000) a štvorciferných čísel, ktoré sú násobkami 36 je stále veľmi veľa (250). Aby sme ich nemuseli všetky skúšať, spíšeme si čo vieme o deliteľnosti čísel a koľko a kde umiestnených jednotiek môžeme v hľadanom čísle mať.
Ak existuje pravidlo, ktoré sa dá aplikovať na všetky násobky čísla x a žiadne číslo, ktoré nie je jeho násobkom toto pravidlo nespĺňa, nazývame ho “pravidlo deliteľnosti číslom x”.
Číslo 36 nie je prvočíslo a nepoznáme žiadne pravidlo deliteľnosti číslom 36, musíme si ho preto rozdeliť na súčin niekoľkých menších deliteľov:
36 = 2 \cdot 18 = 3 \cdot 12 = 4 \cdot 9 = 6 \cdot 6
Pre tieto delitele čísla 36 poznáme pravidlá deliteľnosti:
- 2 - číslo x musí byť párne a teda končiace na cifru 0, 2, 4, 6 alebo 8
- 3 - ciferný súčet musí byť deliteľný číslom 3
- 4 - posledné dvojčíslie (číslo zložené z cifier na mieste desiatok a jednotiek) musí byť deliteľné číslom 4
- 9 - ciferný súčet musí byť deliteľný číslom 9
Pre všetky čísla x, pre ktoré nepoznáme pravidlo deliteľnosti, platí:
Ak poznáme pravidlá deliteľnosti pre nejaké dve čísla, ktoré nie sú deliteľné rovnakým prvočíslom a majú súčin x, potom obe tieto pravidlá spĺňajú jedine všetky násobky čísla x.
Vďaka tomu nám postačí, aby hľadané číslo splnilo pravidlá deliteľnosti čísel 4 a 9.
Čísla, ktoré hľadáme musia mať medzi ciframi len 2 alebo 3 jednotky, pretože číslo 1111 nie je deliteľné 36. Keďže vieme, že 36 je párne, aj hľadané číslo musí byť párne a nemôže sa teda končiť na cifru 1. Usporiadanie cifier 1 v čísle sa nám zníži na 4 možnosti:
- 111_
- 11__
- 1_1_
- _11_
A. 111_
Využijeme pravidlo deliteľnosti číslom 9–ciferný súčet čísla musí byť deliteľný 9timi. Tu vyhovuje len možnosť \mathbf{1116} (1+1+1+6 = 9), ktorá je zároveň deliteľná 4mi, lebo posledné dvojčíslie je 16. Väčší ciferný súčet deliteľný 9timi nevieme pomocou jednej cifry dosiahnuť.
B. 11__
Za chýbajúce cifry musíme doplniť také dve cifry, aby ciferný súčet celého čísla bol deliteľný 9timi a teda sa rovnal 9 alebo 18. Vieme, že 1+1 = 2 a pomocou dvoch cifier získame maximálne 9+9 = 18, takže väčší násobok ako 18 nedosiahneme. To znamená, že súčet neznámych cifier musí byť 9-2 = \mathbf{7} alebo 18-2 = \mathbf{16}. To nám povoluje jednociferné kombinácie 0+7, 1+6, 2+5, 3+4, 7+9 a 8+8. Stále platí, že hľadané číslo je párne a teda, že cifra na mieste jednotiek bude párna. Tomuto kritériu nevyhovuje len kombinácia 7+9. Zo zvyšných kombinácií vieme vytvoriť tieto dvojciferné párne čísla: 70, 16, 52, 34 a 88, pričom len 16, 52 a 88 sú deliteľné 4mi. Po doplnení dostaneme čísla: 1116, 1152 a 1188, z ktorých sme zatiaľ nepoznali \mathbf{1152} a \mathbf{1188}.
C. 1_1_ / D. _11_
Tieto prípady sú veľmi podobné, preto ich vyriešime naraz. Vieme, že aby posledné dvojčíslie bolo deliteľné 4mi, vieme dosadiť na miesto jednotiek iba 2ku alebo 6ku, kvôli jednotke umiestnenej na mieste desiatok. Následne stačí dopočítať chýbajúcu cifru tak, aby ciferný súčet sa rovnal 9 (tentoraz väčší násobok 9ky nie je možný). Dostaneme čísla: (C.) 1512, 1116, (D.) 5112 a 1116, z ktorých sme zatiaľ nepoznali \mathbf{1512} a \mathbf{5112}.
Odpoveď: Našli sme 5 čísel, ktoré vyhovujú podmienkam zo zadania. Sú to čísla \mathbf{1116}, \mathbf{1152}, \mathbf{1188}, \mathbf{1512} a \mathbf{5112}.
Komentár
Väčšina riešiteľov uvažovala nad príkladom správne, odvodili si pravidlá pre deliteľnosť číslom 36, no nie vždy boli tieto pravidlá správne použité alebo nebolo vysvetlené prečo nám postačia.4. príklad
Označme si čísla v jednotlivých trojuholníčkoch ako na obrázku a súčet čísel vo veľkom trojuholníku S.
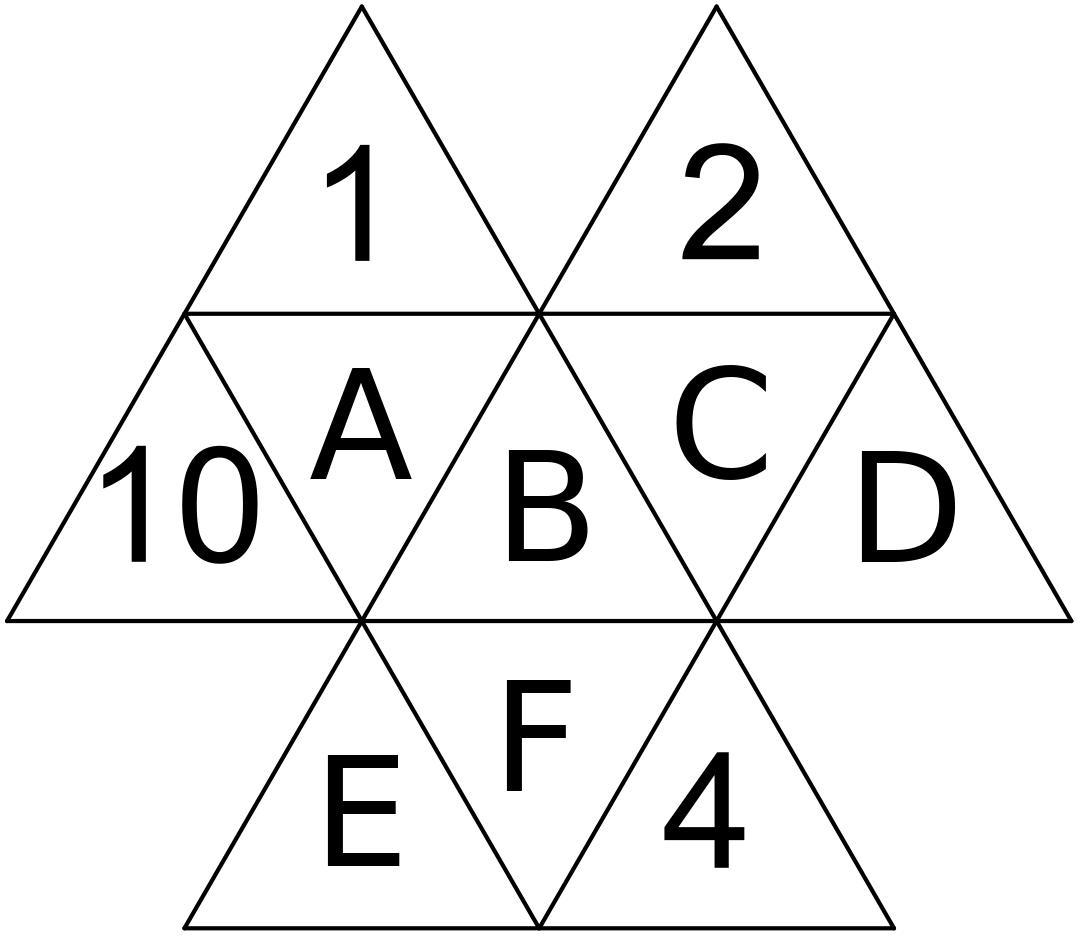 Keď sa pozrieme na súčet súčtov čísel v jednotlivých veľkých trojuholníkoch, ktorý je 3S, tak v ňom započítame každé číslo práve raz, okrem čísla B, ktoré započítame 3-krát.
Keď sa pozrieme na súčet súčtov čísel v jednotlivých veľkých trojuholníkoch, ktorý je 3S, tak v ňom započítame každé číslo práve raz, okrem čísla B, ktoré započítame 3-krát.
Teda dostávame rovnicu:
3S - 2B = 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 + 10 = 55,
ktorú upravíme na:S = \dfrac{55 + 2B}{3}.
Keďže je S celé číslo (čísla v trojuholníčkoch sú len celé čísla, teda aj ich súčet bude celé číslo), tak 55 +2B musí byť deliteľné 3. Keďže zvyšok po delení 3 čísla 55 je 1, tak potom zvyšok čísla 2B po delení 3 musí byť 2. Teda zvyšok B po delení 3 je 1. Podľa zadania tak B môže byť 1, 4, 7 alebo 10. Čísla 1, 4 a 10 už ale máme umiestnené v niektorom z trojuholníčkov, teda B = 7.
Súčet čísel v jednom veľkom trojuholníku je teda S = \frac{55 + 14}{3} = 23. V ľavom hornom veľkom trojuholníku už máme čísla 1, 10 a 7, teda A = 23 - 10 - 1 - 7 = 5.
Z pravého horného veľkého trojuholníka dostávame rovnicu 23 = 2 + 7 + C + D, teda C + D = 14. Keďže nám zostáva umiestniť už len čísla 3, 6, 8 a 9, tak jediná možnosť, ktoré čísla môžu byť C a D je 6 a 8 (je to jedno, v akom poradí).
Zo spodného veľkého trojuholníka dostávame rovnicu 23 = 4 + 7 + E + F, teda E + F = 12. Keďže jediné čísla, čo nám zostali majú súčet 12, tak jediná možnosť, ktoré čísla môžu byť E a F je 3 a 9 (je to jedno, v akom poradí).
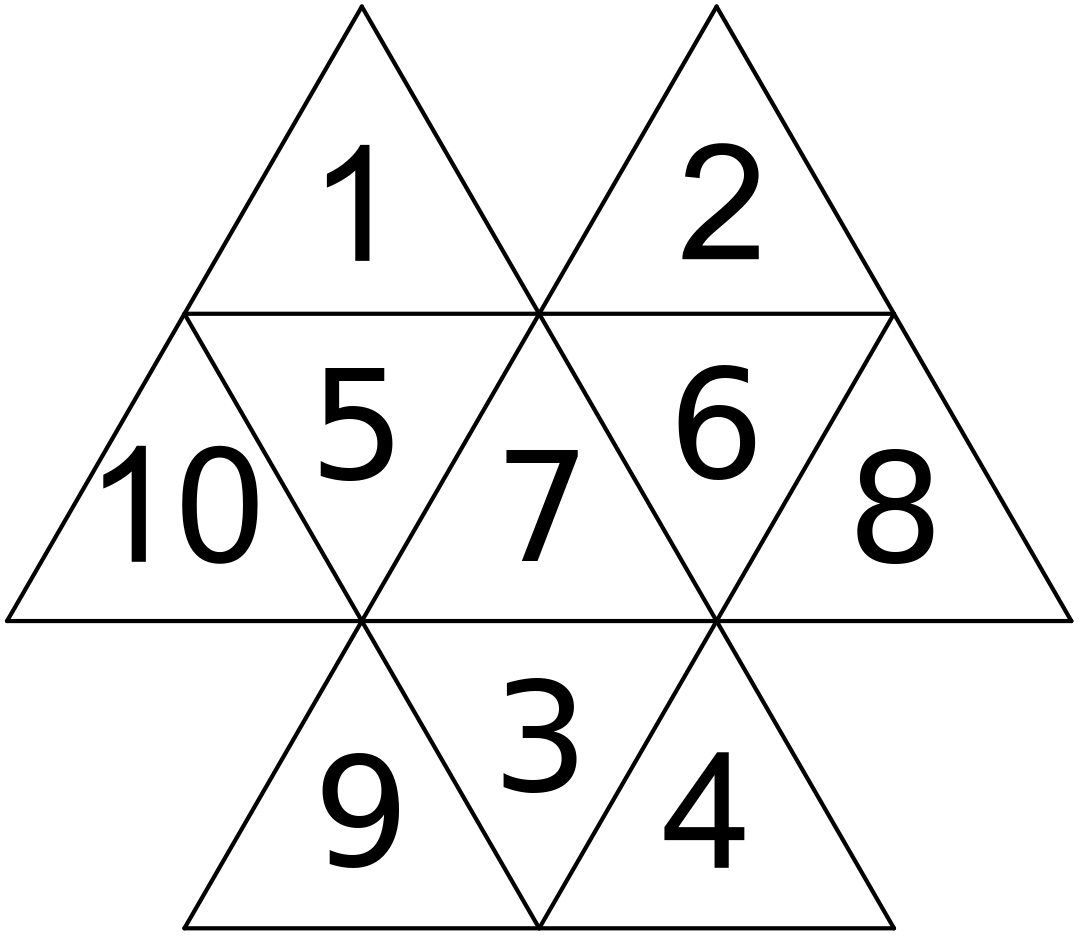
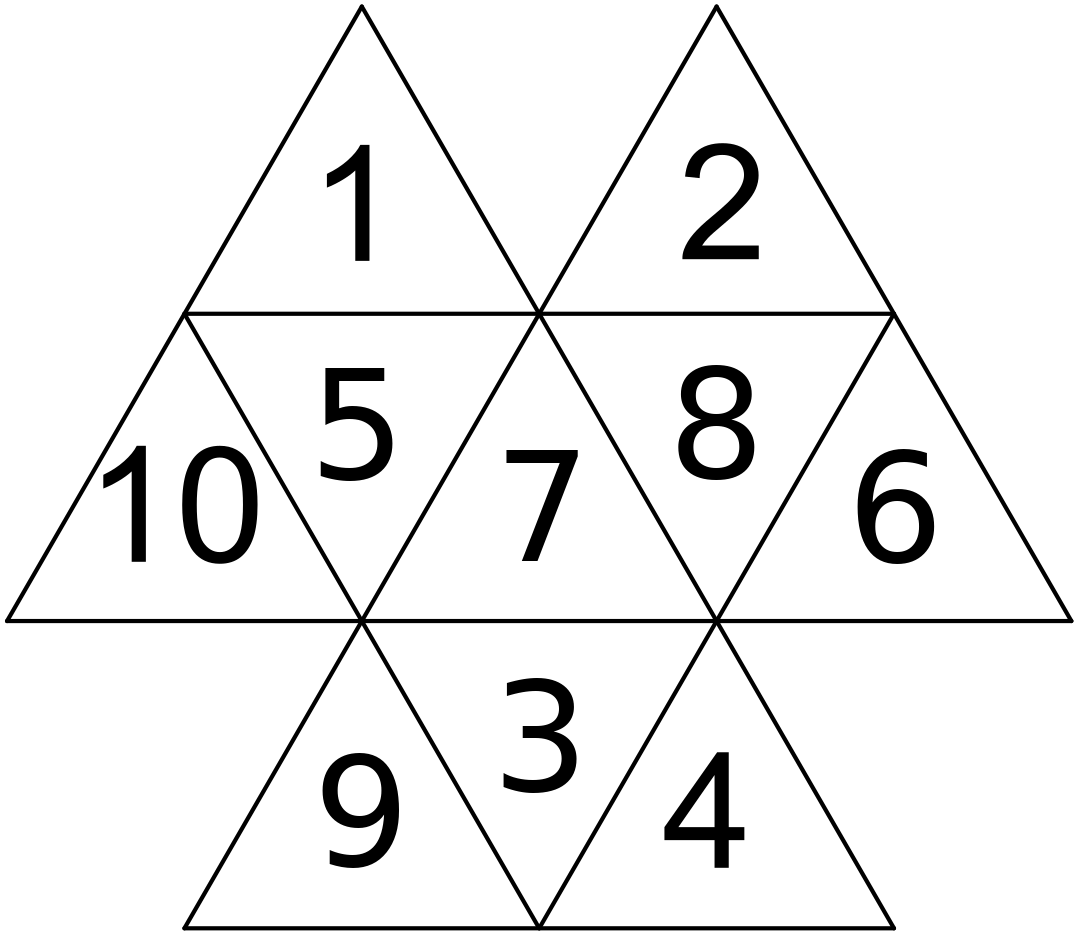
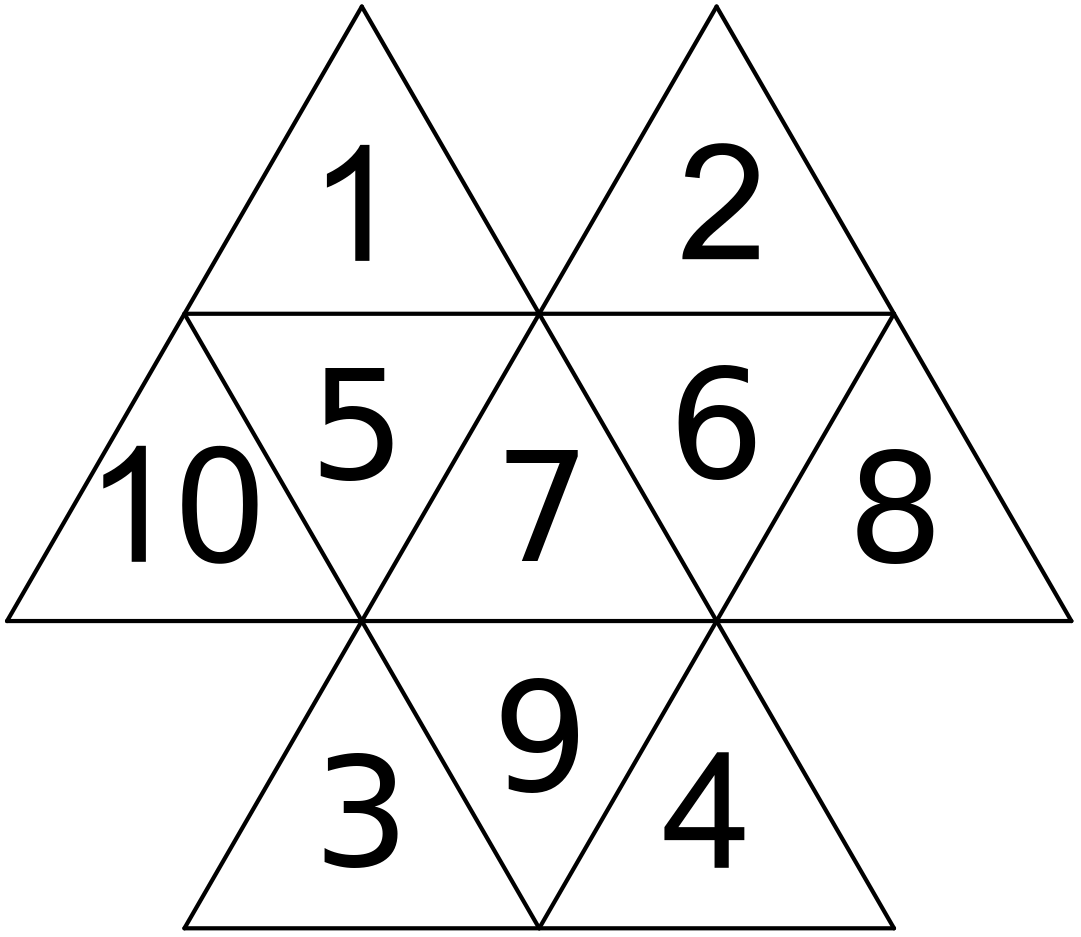
Keďže máme 2 dvojice čísel, ktoré sa navzájom môžu vymeniť, tak dostávame 4 možnosti:
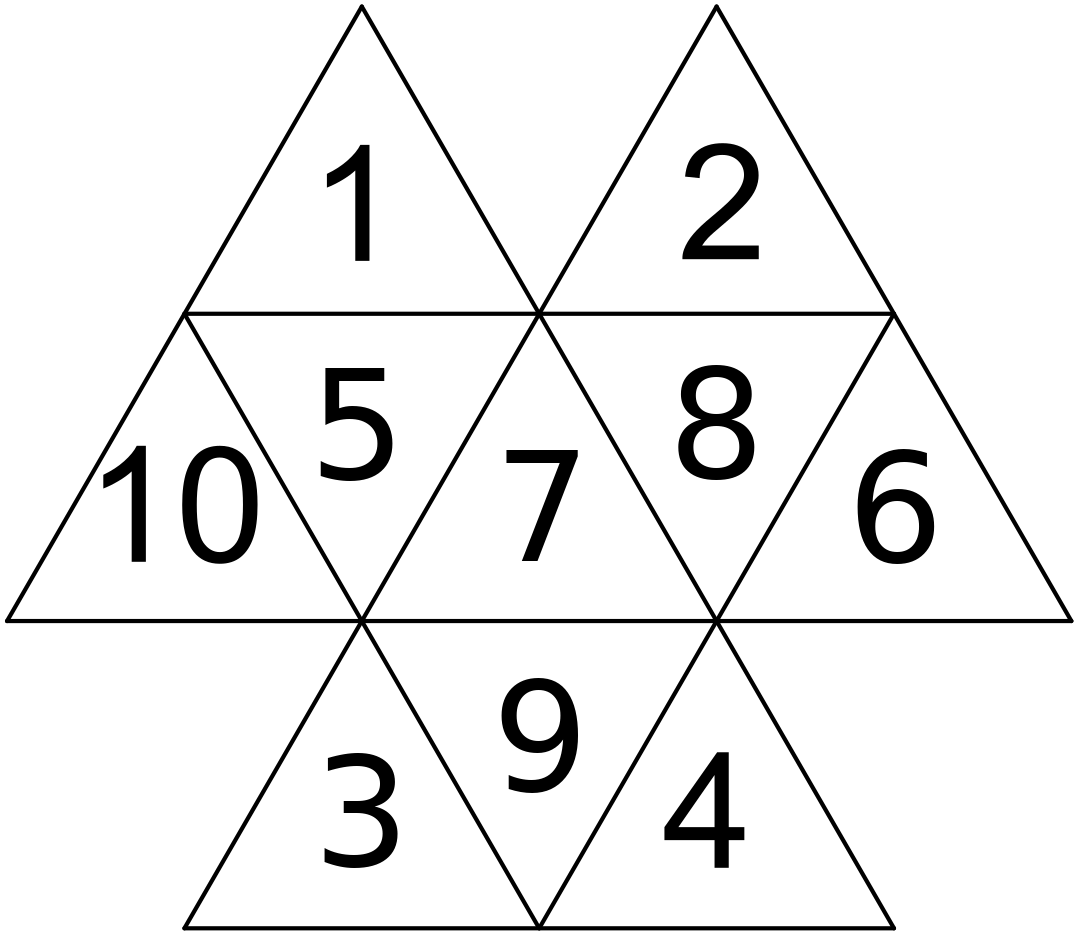
5. príklad
Matky môžu používať tieto dva typy ťahov:
typ:
Korytnačka si zvolí korytnačiatko, ktoré má za sebou alebo na svojej úrovni iné korytnačiatko, a posunie ho o ľubovoľný počet políčok dopredu.typ:
Korytnačka posunie o 1 políčko dopredu všetky korytnačiatka, ktoré za sebou nemajú iné korytnačiatko.
Zamyslime sa nad tým, čo vlastne taká víťazná stratégia je. Je to nejaký jednoznačný postup, ktorým ak sa jeden z hráčov bude riadiť, tak určite vyhrá, bez ohľadu na to, čo bude robiť súper.
Všimnime si, že prehrá hráč, ktorý ako prvý niečo spraví - v tomto prípade umiestni korytnačiatko na deviate políčko s príšerou. Môže nám napadnúť, že pokiaľ druhá matka bude nejakým spôsobom opakovať ťahy po prvej, tak asi nemôže prehrať. Pokiaľ by mala posunúť korytnačiatko na deviate políčko, tak by to len zopakovala po prvej , a teda prvá by už prehrala.
Po tom, ako sme dostali tento nápad, poďme sformulovať našu stratégiu: Pokiaľ prvá matka posunie všetky posledné korytnačiatka o jedno políčko, spraví to aj druhá. Ak posunie jedno korytnačiatko 1. typom z políčka A na políčko B, tak druhá matka posunie nejaké iné korytnačiatko z políčka A na políčko B.
Na to, aby sme ukázali, že táto stratégia vždy funguje, musíme ukázať niekoľko vecí:
Dáka korytnačka prehrá
Ak sa druhá matka bude riadiť vyššie popísanou stratégiou tak neprehrá
Druhá matka sa vždy môže riadiť vyššie popísanou stratégiou
Nejaká korytnačka prehrá
Je jasné, že táto hra nemôže byť nekonečne dlhá a nemôže skončiť remízou, takže dáka korytnačka určite prehrá. Toto je dôležité povedať, lebo nikde ďalej nehovoríme, prečo prvá matka stúpi na prehrávajúce políčko, iba to, že druhá tam stúpi až po prvej.

Ak sa druhá matka bude riadiť stratégiou, tak neprehrá
Uvedomme si, že políčko, na ktorom sa nachádza posledné korytnačiatko, sa 2. typom ťahu môže zmeniť iba o 1. Prvým typom sa nezmení, lebo za posunutým korytnačiatkom vždy aspoň jedno ešte ostane.
Toto znamená, že druhá matka druhým typom ťahu určite žiadne korytnačiatko neposunie na deviate políčko. Pokiaľ totiž druhý typ použije vždy iba po tom, čo ho použila prvá matka, tak ním korytnačiatka vždy posunie na nejaké párne políčko, lebo v posúvaní sa striedajú (po každom pohybe prvej matky nasleduje rovnaký pohyb druhej) a začína prvá posunom na políčko nepárne.
Ani keď prvá matka posunie jedno korytnačiatko z políčka A na políčko B, tak druhá matka neprehrá, pretože tiež posunie korytnačiatko na políčko B, čo nemôže byť 9, lebo potom by prvá matka prehrala prvá.
Môže druhá matka ťah prvej vždy opakovať?
Pokiaľ prvá matka posunie všetky posledné korytnačiatka o 1, tak druhá matka to určite vie spraviť tiež, vždy budú dáke posledné korytnačiatka, ktoré môže posunúť.
A ak prvá matka nejaké korytnačiatko posunie z A na B, tak musí platiť, že na A je ešte aspoň jedna korytnačka, ktorá sa dá pohnúť na políčko B, inak by to druhá matka nevedela zopakovať. Teda ak A je posledné políčko s korytnačiatkami, tak tam musia ostávať ešte aspoň 2.
Na začiatku je na poslednom mieste kde sú korytnačiatka nepárny počet (5) a na ostatných párny (0). Pokiaľ druhá matka vždy opakuje po prvej, tak sa to nikdy nezmení. Korytnačky sa zakaždým hýbu buď v dvojiciach, 2 ubudnú z políčka A a pribudnú na políčko B, teda nezmení sa parita počtu korytnačiek, alebo sa dvakrát pohnú všetky posledné korytnačky o jedno políčko. Posledné políčko s korytnačiatkami sa vlastne spojí s dvomi inými políčkami, a teda ostáva na ňom nepárny počet, keďže na oboch tých políčkach je počet párny.
Takže druhá matka vie zopakovať pohyb korytnačiatkom z políčka A na políčko B vždy, pretože pokiaľ je políčko A posledné políčko s korytnačkami, tak na ňom bol predtým nepárny počet vyšší ako jedna, inak by týmto korytnačiatkom prvá matka mohla hýbať iba druhým typom ťahu. Pokiaľ políčko A nebolo posledné, bol na ňom párny počet, iný ako 0 teda teraz je nepárny a je tam teda aspoň jedna korytnačka, ktorou druhá matka môže pohnúť.
Teda vidíme, že druhá matka určite môže vždy opakovať, a určite pri tom neprehrá.
Komentár
Príklad bol vcelku ťažký takže sme radi, že ste sa s ním popasovali, aj keď ste dostali menej bodov, tak dúfame, že sa vám páčil. Čo sa častých chýb týka, tak viacerí z vás zabudli povedať, prečo druhá matka korytnačka vie opakovať ťahy po prvej. Ide o dôležitú časť, lebo bez nej si nemôžeme byť istý, že nenastane situácia pri ktorej by naša stratégia nehovorila čo má druhá matka spraviť.
6. príklad

Zo zadania vieme, že body A,\, B a C ležia na kružnici. Ich vzdialenosť od S tak bude rovnaká — polomer kružnice. Z toho vyplýva, že trojuholník ASC bude rovnoramenný so záklaňou AC. Takže pre uhly platí | \measuredangle ACS| = | \measuredangle CAS| = 66°. Navyše vieme, že súčet uhlov v trojuholníku je 180°, takže | \measuredangle ASC| = 180° - 2 \cdot 66° = 48°.
Rovnako ako trojuholník ACS, aj trojuholníky ABS a BCS sú rovnoramenné. Navyše majú aj všetky strany zhodne dlhé, keďže sa jedná o pravidelný mnohouholník. Uhly \measuredangle ASB a \measuredangle BSC sú teda rovnako veľké, takže musia byť 24°.
Na obvode kružnice musia byť body daného mnohouholníka rozmiestnené rovnomerne, nakoľko je pravidelný. Uhly okolo bodu S budú tak rovnaké 24° a spolu musia vyplniť 360°. Z toho vyplýva, že sa jedná o 360° : 24° = 15-uholník.
Odpoveď: Hľadaný mnoholuholník má 15 vrcholov.
7. príklad
Zopakujme si najprv, čo vieme povedať o cifrách nejakého čísla, keď vieme, čím je deliteľné.
- Ak je číslo párne, tak jeho posledná číslica musí byť párna.
- Ak je číslo deliteľné tromi, tak je aj súčet jeho cifier deliteľný tromi.
- Ak je číslo deliteľné piatimi, tak jeho posledná cifra musí byť 0 alebo 5.
- Ak je číslo deliteľné ôsmimi, tak jeho posledné trojčíslie je deliteľné ôsmimi.
Ak je číslo \overline{cbabc} deliteľné 15, tak je deliteľné aj 3 aj 5 (lebo 15 je deliteľné aj 3 aj 5). Podľa deliteľnosti piatimi vieme, že jeho posledná číslica, čo je c, musí byť 0 alebo 5. Zo zadania ale vieme, že všetky číslice sú nenulové, takže c=5.
Okrem toho podľa deliteľnosti tromi vieme, že a+b+c aj c+b+a+b+c sú deliteľné tromi. Preto aj ich rozdiel, teda b+c, musí byť deliteľný tromi. Navyše aj rozdiel a+b+c a b+c, čiže a, musí byť deliteľný tromi.
Ďalej vieme, že \overline{abcba} je deliteľné ôsmimi, a teda musí byť párne (lebo aj 8 je párna). Jeho posledná číslica, čo je a, teda musí byť párna.
Zatiaľ sme si teda povedali, že c=5, a že b+c je deliteľné tromi. To platí, keď je b rovné 1, 4, alebo 7.
Zistili sme aj to, že a je párne aj deliteľné tromi, a ešte podľa zadania nemôže byť 0. Ostáva nám teda len jedna možnosť, a=6.
Máme teda tri možnosti, čo môže byť \overline{abc}: 615, 645, a 675. Overíme, či pre tieto čísla naozaj platia všetky podmienky zo zadania. Zistíme, že pre prvé dve z nich neplatí podmienka o deliteľnosti ôsmimi, čo nám necháva len jediné riešenie: \overline{abc}=675.
Iné riešenie
Rovnako ako pri prvom riešení zistíme, že c=5. Teraz využijeme, že pravidlo o deliteľnosti tromi (ako aj tie ostatné z nich) platí aj opačne: ak je ciferný súčet čísla deliteľný tromi, tak je aj samotné číslo deliteľné tromi. Vieme, že \overline{abc} je deliteľné tromi, a má rovnaký ciferný súčet ako \overline{cba}, takže aj \overline{cba} je deliteľné tromi.
Okrem toho je \overline{abcba} deliteľné ôsmimi, takže jeho posledné trojčíslie, čo je \overline{cba}, je deliteľné ôsmimi.
Keďže je \overline{cba} deliteľné tromi aj ôsmimi, tak musí byť deliteľné aj ich najmenším spoločným násobkom, čo je 24. Už vieme, že c=5, a trojciferných násobkov 24, ktoré začínajú číslicou 5, nie je až tak veľa.
Konkrétne sú to 504, 528, 552, a 576. Vyskúšame si teda za \overline{cba} dosadiť každé z týchto čísel (504 neberieme do úvahy, lebo v správnom riešení nemôže byť číslica 0), a overíme, či naozaj platia všetky podmienky. Pre 528 a 552 neplatí deliteľnosť pätnástimi, takže nám vyjde jediné riešenie \overline{abc}=675.
Komentár
Väčšine z vás úloha nerobila problém a našli ste správne riešenie, aj keď niekedy ste si menej zúžili možnosti pre jednotlivé číslice, takže ste museli skúšať viac možností. Okrem toho viacerí z vás zabudli, že podľa zadania musia byť všetky číslice nenulové, a mohli vám vyjsť výsledky navyše, ale za to sme nakoniec nestrhávali body.
8. príklad

Keďže body A_1, B_1, C_1 sú stredmi strán \triangle ABC, tak úsečky A_1B_1, A_1C_1, B_1C_1 sú jeho stredné priečky. Na základe toho vieme povedať niekoľko vecí. Stredná priečka trojuholníka je rovnobežná so stranou trojuholníka, ktorej stred sa na nej nenachádza, pričom dĺžka tejto strednej priečky sa rovná polovici dĺžky rovnobežnej strany. Keďže \triangle ABC je rovnostranný, všetky jeho stredné priečky budú mať dĺžku rovnú polovici strany. Taktiež všetky tri stredné priečky trojuholníka rozdieľujú trojuholník na 4 zhodné rovnostranné trojuholníčky (keďže veľký a malý trojuholník sú podobné v pomere 1:2).
Keďže obsah trojuholníka sa dá vypočítať ako polovica súčinu strany a výšky kolmej na túto stranu, obsah dvoch trojuholníkov bude rovnaký, keď budú mať rovnako dlhú stranu a výšku. Teraz si môžeme všimnúť, že \triangle A_1C_1M a \triangle A_1C_1B_1 rovnakú stranu (úsečku A_1C_1). Vieme, že A_1C_1 je rovnobežné s AC a body M a B_1 ležia na úsečke AC. To znamená, že kolmica na úsečku A_1C_1 z bodu M a z bodu B_1 je rovnako dlhá, lebo vzdialenosť medzi rovnobežnými úsečkami je rovnaká. Takže \triangle A_1C_1M a \triangle A_1C_1B_1 majú rovnako dlhú aj stranu, aj výšku na ňu. Dostávame, že S_{\triangle A_1C_1M} = S_{\triangle A_1C_1B_1}. Keďže \triangle A_1B_1C je zhodný s \triangle A_1B_1C_1, tak S_{\triangle A_1B_1C} = S_{\triangle A_1C_1M} .
Podobne sa dá ukázať, že S_{\triangle A_1KB_1} = S_{\triangle A_1KC_1} , keďže majú rovnakú stranu (úsečku A_1K) a majú rovnako dlhú výšku (vzdialenosť medzi rovnobežnými úsečkami BC a B_1C_1).
Štvoruholník A_1MC_1K sa skladá z \triangle A_1C_1M a \triangle A_1KC_1 , takže
S_{\triangle A_1MC_1K}= S_{\triangle A_1C_1M} + S_{\triangle A_1KC_1}.
Ďalej trojuholník B_1KC sa skladá z \triangle A_1B_1C a \triangle A_1KB_1 , čiže
S_{\triangle B_1KC} = S_{\triangle A_1B_1C} + S_{\triangle A_1KB_1}.
Ako už vieme, S_{\triangle A_1C_1M} = S_{\triangle A_1B_1C} , rovnako ako aj S_{\triangle A_1KC_1} = S_{\triangle A_1KB_1} , takže aj ich súčet, teda mnohouholníky A_1MC_1K a B_1KC musia mať rovnaký obsah. Oba mnohouholníky obsahujú trojuholník s vrcholmi A_1, K a S (priesečník úsečiek A_1M a B_1K). Nakoniec odčítaním obsahu \triangle A_1KS od mnohouholníkov A_1MC_1K a B_1KC , získame, že aj S_{\triangle KSMC_1} = S_{\triangle BSA_1C}.
Teda sme dokazali, že štvoruholníky zo zadania musia mať rovnaký obsah.
9. príklad
Postup, ktorý budeme používať, je takzvaný dôkaz sporom. T.j. budeme predpokladať, že dokážeme ofarbiť vrcholy bez toho, aby sme dostali rovnoramenný trojuholník, a dostaneme sa do sporu, teda do nemožnej situácie. V takom prípade jediná ostávajúca možnosť bude, že sa rovnoramennému trojuholníku vyhnúť nevieme, a teda budeme hotoví.
Ako prvé si môžeme všimnúť, že musíme mať dva vrcholy rovnakej farby pri sebe. Predpokladajme, že by nemuseli byť dva body rovnakej farby vedľa seba. V tom prípade musíme farby striedať medzi modrou a červenou farbou. Toto bude fungovať dobre na prvých dvanásť bodov, lenže trinásty bod v tejto chvíli susedí aj s modrým aj s červeným bodom. Teda dvojica susedných bodov rovnakej farby existuje.
Teraz sa pozrieme na túto jednofarebnú dvojicu susediacich vrcholov. Keďže na konkrétnej farbe nezáleží, nech je táto dvojica červenej farby. Pre väčšiu prehľadnosť (a keďže situácia sa dá vhodne otočiť) bude táto dvojica bodov pozostávať z bodov A, B, ako na obrázku:

Pozrime sa teraz na body C, H, M a prislušné trojuholníky, ktoré tvoria spolu s bodmi A, B. Tieto tri trojuholníky vidíme prerušovanými čiarami na obrázku. Vzhľadom na to, že náš trinásťuholník je pravidelný, ľahko vidíme, že tieto tri trojuholníky sú rovnoramenné. Keďže sme predpokladali, že rovnoramenný trojuholník jednej farby neexistuje, musia byť všetky tieto tri body nutne modrej farby.
Lenže to sa nesmie stať. Trojuholník MCH je sám totiž rovnoramenný. Dostali sme sa teda do sporu, tak ako sme chceli.
Zhrnutie a záver:V našom riešení sme najprv predpokladali, že ofarbenie bez rovnoramenného trojuholníka existuje. Potom sme logickými krokmi dospeli ku sporu, keď nám nutnosťou taký trojuholník vznikol. Takže náš predpoklad, že rovnoramenný trojuholník nemusí existovať, bol nesprávny. Dokázali sme teda, že rovnoramenný trojuholník musí existovať, presne tak ako sme mali.
Komentár
Viacerí z vás ste príklad zvládli na plný počet bodov, no vyskytli sa dva najčastejšie typy chýb.
Prvý z nich bol, že ste postupovali približne týmto riešením a ukázali ste, že máme nejaký bod, ktorý sa nedá ofarbiť ani jednou farbou. Lenže tu treba ukázať aj to, že tento bod je rozumne definovaný a taktiež, že je to jeden z bodov trinásťuholníka.
Druhý typ chyby sa vyskytoval pri riešeniach typu "skúšame všetky možnosti". Tento postup je síce matematicky správny, ale na získanie plného počtu bodov treba ukázať, že ste vyskúšali naozaj všetky (relevantné) možnosti. Bez toho, a hlavne keď napíšete iba "tu som skúšal možnosti a vyšlo ___", môžete dostať iba malý počet bodov.
10. príklad

Na obrázkoch vidíme rozdelenie trojuholníka pre n postupne 4,\, 6,\, 8. Nie je náročné uvedomiť si, že keď máme dve rozdelenia rovnostranného trojuholníka na a a b častí, tak vieme vyrobiť rozdelenie na a+b-1 častí. Na nasledovnom obrázku je ilustované ako presne:

Jednoducho vezmeme nejaký z menších rovnostranných trojubolníkov v rozdelení na b častí a vpíšeme do neho rozdelenie pre a častí. Takto dostaneme rozdelenie na a+b-1 častí, lebo b-1 trojuholníkov sme nezmenili a jeden sme rozdelili na a častí. Keďže vieme získať rozdelenia na 4,6,8 častí, tak vieme získať aj všetky rozdelenia tvaru 4+3k_1,\, 6+3k_2,\, 8+3k_3 pre prirodzené čísla k_1,\, k_2,\, k_3. Stačí vždy skombinovať rozdelenie na b častí s rozdelením na 4 časti čím získame rozdelenie na b+3 časti.
Každé prirodzené číslo okrem čísel 2,\, 3,\, 5 vieme zapísať ako n+3k pre n \in \{4,6,8\} a nezáporné celé číslo k. Chceli sme teda dokázať, že rovnostranný trojuholník nejde rozdeliť na 2,\, 3 alebo 5 častí. Nech delíme rovnostranný trojuholník hociako, tak vždy bude mať vo svojich vrcholoch tri rovnostranné trojuholníky. Dá sa na to pozerať tak, že je iba jedna možnosť, ako môže byť vrchol pôvodného rovnostranného trojuholníka zároveň vrcholom nejakého trojuholníka v rozdelení a musí nastať delenie, teda každý vrchol pôvodného trojuholníka musí byť vrcholom iného rovnostranného trojuholníka v rozdelení.

Tento obrázok ilustruje situáciu popísanú vyššie, ktorá nastane v každom jednom rozdelení. Vidíme, že je nutné aby malo každé rozdelenie aspoň 4 časti, teda nevieme rozdeliť rovnostanný trojuholník na 2 ani 3 menšie rovnostranné trojuholníky. Teraz ostáva už len prípad n = 5. Pre jednoduchosť časť rozdelenia neobsahujúcu tri trojuholníky pri vrcholoch pôvodného trojuholníka nazvime Stredná časť.
- Ak je obvod Strednej časti päť- alebo šesťuholník, tak ju nevieme rozdeliť na dva trojuholníky, teda ani na dva rovnostranné trojuholníky.
- Ak je Stredná časť štvoruholník, tak musí ísť o lichobežník. To preto, lebo jediný spôsob, ako vieme znížiť počet vrcholov na obvode Strednej časti, je zrušiť stranu medzi nejakými dvoma vrcholmi. To docielime tým, že sa nejaké trojuholníky pri vrcholoch pôvodného začnú dotýkať a teda pokryjú celú stranu. Príklad môžeme vidieť na nasledovnom obrázku:
Vyjde lichobežník, keďže strany trojuholníkov pri vrcholoch pôvodného trojuholníka sú rovnobežné so stranami pôvodného trojuholníka. Jediný problém však je, že jediný štvoruholník, ktorí sa dá rozdeliť na dva rovnostranné trojuholníky je kosoštvorec s uhlami pri vrcholoch veľkými 60^\circ,120^\circ,60^\circ, 120^\circ, kým náš lichobežník bude mať uhly 60^\circ vedľa seba.
- Ak je Stredná časť trojuholník, tak musí ísť o rovnostranný trojuholník. Stany tohto trojuholníka totiž musia byť rovnobežné so stranami pôvodného trojuholníka, ktorí sme začali deliť. Rovnostranný trojuholník však nejde rozdeliť na dve časti, teda sme hotoví.
Prémia 1
Najlepšie riešenie pozostávalo zo 68 ťahov. V tabuľke vidíme jedno z takýchto riešení. Čísla postupne ukazujú o koľký ťah ide, pričom červenou farobu sú značené ťahy koňa, modrou ťahy vyhadzovacieho pešiaka, a zelenou ťahy narážacej veže. Skokana toto riešenie nepoužíva.
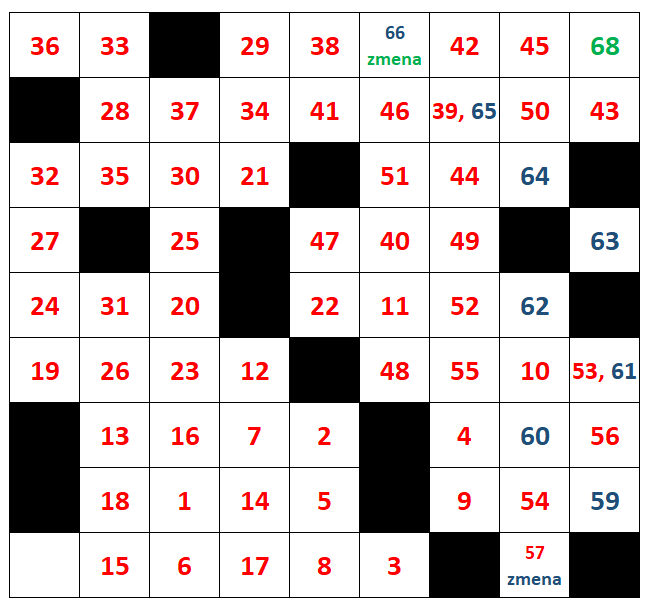
Komentár
Často sa stávalo, že v riešeniach boli vynechané niektoré políčka alebo sa vyskytli pohyby figúrkou na políčko kam sa daná figúrka pohnúť nemôže. Tieto chyby sme hodnotili tak, že sme ku počtu ťahov ktoré riešiteľ dosiahol pripočítali ako penalizáciu 10 ťahov, čo je počet, na ktorý sa jednoduchým spôsobom dá z ľubovoľného políčka dostať na hociktoré iné.
Bodovanie
- 68 ťahov - 7 bodov
- 69 až 70 ťahov - 6 bodov
- 71 až 73 ťahov - 5 bodov
- 74 až 77 ťahov - 4 body
- 78 až 85 ťahov - 3 body
- 86 až 105 ťahov - 2 body
- 106 a viac ťahov - 1 bod