Vzorové riešenia 3. kola
1. príklad
Označíme si O = lampové oleje, La = laná, B = bomby a Le = leukoplasty. Teraz si zapíšeme nerovnice zo zadania: Le \gt La a B \gt O (túto nerovnicu sme otočili oproti tej v zadaní, aby sme lepšie videli, že čísla, ktorých súčet hľadáme sú menšie).
Keďže hľadáme súčet dvoch menších čísiel (La a O sú menši ako Le a B) a poznáme súčet všetkých (30), tak vieme, že súčet La + O bude menej ako polovica, teda La + O \lt 30 : 2 = 15.
Taktiež vieme, že všetky čísla sú nepárne, z čoho vyplýva, že rozdiel medzi dvomi jednotlivými číslami bude minimálne 2. Podľa toho upravíme pôvodné nerovnice na Le \geq La + 2 a B \geq O + 2. Vidíme, že Le + B \geq La + O + 4.
Teraz si skúsime za La + O doplniť najväčšie možné číslo - 14:
Le + B \geq La + O + 4 \\ Le + B \geq 14 + 4 \\ Le + B \geq 18
Teraz nám ale vychádza celkový súčet 18 + 14 = 32, čo je moc veľa. A keďže Le + B môže byť v tomto prípade iba väčšie, tak teraz zoberieme menšie La + O, čo je 12 (keďže rozdiel medzi dvoma nepárnymi číslami je minimálne 2). A v tomto prípade nám všetko vychádza: 18 + 12 = 30 a máme aj najväčie možné La + O, lebo sme išli od najväčších možností.
Odpoveď: Lychondražej si mohol kúpiť dokopy najviac 12 lán a olejov.
2. príklad
Keď sa pozrieme na príklad a vidíme v ňom veľké množstvo neznámych a nejaké pomery medzi nimi, tak nás to navádza na riešenie pomocou rovníc. Dá sa to riešiť aj tak opisne, no väčšinou ide iba o slovný zápis rovností, v ktorom sa dá často ľahšie stratiť.
Tak, máme už predstavu, že príklad chceme vyriešiť pomocou rovníc. Najprv ich teda musíme zostaviť.
Základ je označiť si písmenkami veci, ktoré nepoznáme. Nevieme koľko stáli sandále, tak si ich hodnotu označme S. Nepoznáme koľko peňazí mal Lychondražej vo vreckách tak, to množstvo si označme V a nakoniec nevieme koľko peňazí mal na účte - U.
Máme 3 neznáme. Rovnice majú často takú vlastnosť, že aby sme ich vedeli vypočítať potrebujeme ich aspoň toľko, koľko je premenných. Tak sa zo zadania pokúsme zostaviť tri rovnice, v ktorých budú vystupovať naše 3 neznáme:
Zaplatením \frac{4}{11} ceny sandál minul Lychondražej štvrtinu peňazí na účte, čo si vieme prepísať ako:
\dfrac{4}{11}S=\dfrac{1}{4}U
Keď Lychondražej zaplatil \frac{7}{11} ceny sandál z vreciek, tak mu v nich ostalo 99 peňazí. Potom \frac{7}{11} ceny sandál je rozdiel medzi počtom peňazí vo vreckách pred zaplatením a po zaplatení:
\dfrac{7}{11}S=V-99
Nakoniec vieme, že pomer peňazí vo vreckách a na účte bol 5:2:
\dfrac{V}{U}=\dfrac{5}{2}
No a týmto už príklad máme takmer vypočítaný, stačí nám iba úpravou rovníc vyjadriť S. Chceme vytvoriť 1 rovnicu, kde budeme mať iba konštanty, čísla, a cenu sandál. Z tretej rovnice vieme zistiť, koľkokrát viac peňazí mal Lychondražej vo vreckách ako na účte. Po vynásobení oboch strán hodnotou U dostávame:
V=\dfrac{5}{2}U
To vieme dosadiť do 2. rovnice namiesto V:
\dfrac{7}{11}S=\dfrac{5}{2}U-99
No a z 1. rovnice vynásobením oboch strán štyrmi zistíme, koľkokrát je hodnota peňazí na účte väčšia ako hodnota sandál:
\dfrac{16}{11}S=U
To vieme dosadiť do predchádzajúcej rovnice namiesto U a dostávame hľadaný tvar:
\dfrac{7}{11}S=\dfrac{5}{2}\cdot\dfrac{16}{11}S-99
Keď máme jednu rovnicu o jednej neznámej, tak už nás toho veľa nečaká, no aj pri tom treba mať nejaký postup, nech sa nezamotáme. Najprv je dobré roznásobením zbaviť rovnicu zlomkov, a potom dostať všetky členy, kde sa nám vyskytla neznáma na jednu stranu:
\dfrac{7}{11}S=\dfrac{5}{2}\cdot\dfrac{16}{11}S-99
\dfrac{7}{11}S=\dfrac{40}{11}S-99
Po vynásobení 11-timi:
7\cdot S=40\cdot S-99\cdot11
99\cdot11=33\cdot S
1089=33\cdot S
1089 : 33=S
S=33
Tak, a máme výsledok.
Odpoveď: Sandále stáli 33 peňazí.
3. príklad
Zaveďme si označenie podľa prvých písmen z mien. Teda Adenei budeme označovať A, Bordiko budeme volať B, Cyntervel označíme C a Drlpian označíme D.
Jeden zo spôsobov, ako sme sa mohli na príklad pozrieť, bolo spýtať sa, kto by vlastne mohol hovoriť pravdu.
Pozrime sa na prípad, že by A hovoril/a pravdu. Kto môže mať potom pravdu okrem A?
- B tvrdí že je na najvyššom poschodí. Na najvyššom poschodí je ale A, B teda klame.
- C tvrdí, že žiaden kapitán nie je pod A. Kapitáni sú práve dvaja a A je na najvyššom poschodí, aspoň jeden kapitán teda určite bude pod A. Preto C určite klame.
- D tvrdí že C hovorí pravdu, čo nemôže byť pravda, D teda klame.
Ukázali sme, že keby A hovoril/a pravdu, B, C aj D musia klamať. Zo zadania ale vieme, že máme dvoch ľudí, ktorí hovoria pravdu, a dvoch, ktorí klamú. Preto A nemôže hovoriť pravdu, takže klame.
Čo ak B hovorí pravdu?
- A vždy klame, ako sme ukázali vyššie.
- C tvrdí, že všetci kapitáni klamú. B je ale kapitán a hovorí pravdu, C teda klame.
- D hovorí, že C má pravdu. C ale klame, a tak klame aj D.
Keby B hovorilo pravdu, A, C aj D klamú. To ale nemôže nastať, keďže klamú iba dvaja a dvaja hovoria pravdu. B teda klame.
Keď A aj B klamú, C a D musia kvôli tomu, aby sme mali dva pravdivé výroky, hovoriť pravdu. C tvrdí, že všetci kapitáni klamú. Kapitáni aj klamári sú dvaja, a to A a B. Zostali dve kapitánky, nimi sú C a D.
Podľa C nie je pod A žiaden kapitán. Podľa D nie je pod A žiadna kapitánka. Pod A nikto nie je, takže je na najnižšom z poschodí.
D je podľa C tesne pod C, teda určite nie je najvyššie. B tvrdí že je kapitán a je najvyššie, zároveň ale vieme, že klame. To, že je kapitán, vieme od C, musí teda klamať v tom, že je na najvyššom poschodí. Jediná osoba, ktorá môže byť na vrchnom poschodí, je teda C.
Podľa C je potom D tesne pod ňou. Pre B už zostalo iba druhé najnižšie poschodie.
Poradie poschodí je teda takéto:
- (najvyššie) C, je to kapitánka a hovorí pravdu,
- D, je to kapitánka a hovorí pravdu,
- B, je to kapitán a klame,
- A, je to kapitán a klame.
Komentár
Úloha sa dala riešiť mnohými spôsobmi. Namiesto toho, aby sme sa pozerali na to, či môžu hovoriť pravdu jednotlivci, sme sa napríklad mohli pozerať na dvojice a zisťovať, či môžu nejakí dvaja ľudia hovoriť naraz pravdu. Týmto postupom by sme rýchlo došli k tomu, že jediná dvojica, ktorá môže hovoriť pravdu je C a D.
Pomerne častou chybou bolo vyhlásenie, že keď C hovorí pravdu, aj D hovorí pravdu. To by nemuselo vždy platiť. Ak by nejaká kapitánka strážila nižšie poschodie ako A, D by klamal napriek tomu, že mal pravdu v tom, že má C pravdu.
4. príklad
Najskôr sa chce Lychondražej dostať z pravého dolného rohu do ľavého horného rohu bludiska. Pri tom sa môže presúvať iba smerom na západ alebo smerom na sever. Práve 10 chodieb teda musí prejsť smerom na západ a práve 10 chodieb smerom na sever. Celkovo teda musí prejsť 20 chodbami.
Ak prejde 20 chodbami, musí prechádzať cez 21 miestností, s tým, že v začiatočnej miestnosti (vpravo dole) sa nehýbe. Tým pádom prejde teda cez 19 miestností, v ktorých sa bude otáčať a skončí v miestnosti v ľavom hornom rohu bludiska. V tejto miestnosti sa následne otočí a pokračuje cestou späť do pravého dolného rohu bludiska. Cestou späť prejde 10 chodieb na východ a 10 chodieb na juh. Opäť teda prejde 20 chodbami a 19 miestnosťami (ak nepočítame miestnosť vľavo hore). Potom príde do miestnosti v pravom dolnom rohu, kde sa už neotáča.
Celkovú dĺžku cesty tým pádom vypočítame ako súčet dĺžok chodieb, ktorými prechádzal, to je \left(20+20\right)\cdot10 = 400, plus súčet otáčaní sa v miestnostiach. Lychondražej môže vyjsť 2 východmi zo začiatočnej miestnosti: buď na západ – ten si označme ako východ A, alebo na sever – ten si označme ako východ B. Vchody do miestnosti v ľavom hornom rohu bludiska si označme C, D (ako na obrázku).

Uvedomme si, že ak je v priebehu cesty Lychondražej otočený na západ a otočí sa doprava, zmení smer zo západu na sever. Ak je otočený na sever, už sa nemôže otočiť doprava smerom na východ (cestou tam môže chodiť len na západ alebo na sever). Podobne ak je otočený na sever, môže sa otočiť doľava na západ. Ak je otočený na západ, už sa nemôže otočiť doľava na juh.
Otočenie doprava je proti smeru hodinových ručičiek, prejde preto \frac{1}{4} kruhu, čiže 1 meter. Otočenie doľava je v smere hodinových ručičiek, musí ísť teda opačným smerom. Tým pádom prejde \frac{3}{4} kruhu, čiže 3 metre. Ak pôjde rovno, prejde \frac{2}{4} kruhu, teda 2 metre.
Ak sa Lychondražej otočí doprava a potom otočí doľava \left(1 + 3\right), prejde rovnakú dĺžku ako keby išiel 2-krát rovno \left(2 + 2\right). Na 1 miestnosť nám potom pripadajú 2 metre. Nezáleží teda na tom, koľkokrát pôjde doprava a koľkokrát pôjde doľava, ale záleží nám na tom, o koľko krát viac sa v priebehu cesty otočí doprava ako doľava.
Ak Lychondražej vyjde z pravej dolnej miestnosti východom A a vojde do ľavej hornej miestnosti vchodom C, vychádzať bude smerom na západ a vchádzať smerom na sever. Preto sa bude musieť otočiť doprava o 1 krát viac ako sa otočí doľava. Na 18 miestností budú pripadať 2 metre a zostane nám jedna otočka doprava, ktorá má 1 meter. Dokopy 18\cdot2+1 = 37 metrov.
Ak vyjde východom A a vojde vchodom D, tak sa otočí rovnako veľa krát doprava ako doľava. Na všetkých 19 miestností budú pripadať 2 metre. Dokopy 19 \cdot2 = 38 metrov.
Takisto ak vyjde východom B a vojde vchodom C, potom sa otočí rovnako veľa krát doprava ako doľava. Takisto prejde dokopy 19 \cdot 2 = 38 metrov.
Ak vyjde východom B a vojde vchodom D, pri tejto ceste sa bude musieť otočiť doľava o 1 krát viac ako sa otočí doprava. Na 18 miestností budú pripadať 2 metre a zostane nám jedna otočka doľava, ktorá má 3 metre. Dokopy 18\cdot2+3 = 39 metrov.
| Východ | Vchod | Otočenie po ceste | Celková dĺžka úseku |
|---|---|---|---|
| A | C | doľava - 1 \, \text{m} | 18\cdot2+1=37 \, \text{m} |
| A | D | rovno - 2 \, \text{m} | 18\cdot2+2=38 \, \text{m} |
| B | C | rovno - 2 \, \text{m} | 18\cdot2+2=38 \, \text{m} |
| B | D | doprava - 3 \, \text{m} | 18\cdot2+3=39 \, \text{m} |
Poďme sa pozrieť ako bude vyzerať Lychondražejovo blúdenie v ľavom hornom rohu. Keď príde do ľavého horného rohu z cesty C môže sa buď otočiť o 4 metre a ísť naspäť cestou C, alebo sa otočiť o 1 meter a ísť naspäť cestou D.
Ak príde do ľavého horného rohu z cesty D môže sa buď otočiť o 4 metre a ísť naspäť cestou D, alebo sa otočiť o 3 metere a ísť naspäť cestou C. (celkovo vyjde narovnako či rátame, že môže prejsť aj 0 metrov a rovno sa vrátiť späť alebo nie)

Už nám iba zostáva sa pozrieť na cestu späť. Pri nej si môžeme celú plochu otočiť o 180 stupňov a chodiť iba tak ako počas cesty smerom tam, potom sa na cestu z východu C do A vieme pozerať ako na pôvodnú cestu z B do D, na cestu z C do B ako na cestu z B do C. Podobne cesta z D do A zodpovedá pôvodnej ceste z A do D a nakoniec cesta z D do B je taká istá ako cesta z A do C.
| Východ | Vchod | Otočenie po ceste | Celková dĺžka úseku |
|---|---|---|---|
| C | A | doprava - 3 \, \text{m} | 18\cdot2+3=39 \, \text{m} |
| C | B | rovno - 2 \, \text{m} | 18\cdot2+2=38 \, \text{m} |
| D | A | rovno - 2 \, \text{m} | 18\cdot2+2=38 \, \text{m} |
| D | B | doľava - 1 \, \text{m} | 18\cdot2+3=37 \, \text{m} |
Poďme sa pozrieť na všetky úseky cesty, ktorých dĺžky postupne sčítame, čím dostaneme celkovú vzdialenosť prejdenú Lychondražejom. Nezabudnime však na vzdialenosť 400 metrov, ktorú Lychondražej nachodil v chodbách. Tú rovno zarátame do konečného súčtu, keďže pre každú dvojicu vchodu a východu je rovnaká.
| Cesta tam | Otočenie | Cesta späť | Súčet |
|---|---|---|---|
| A \rightarrow C = 37 \, \text{m} | C \rightarrow C = 4 \, \text{m} | C \rightarrow A = 18\cdot2+3 = 39 \, \text{m} | 80 + 400 \, \text{m} |
| C \rightarrow B = 19\cdot2 = 38 \, \text{m} | 79 + 400 \, \text{m} | ||
| C \rightarrow D = 1 \, \text{m} | D \rightarrow A = 19\cdot2 = 38 \, \text{m} | 76 + 400 \, \text{m} | |
| D \rightarrow B = 18\cdot2+1 = 37 \, \text{m} | 75 + 400 \, \text{m} | ||
| A \rightarrow D = 38 \, \text{m} | D \rightarrow C = 3 \, \text{m} | C \rightarrow A = 18\cdot2+3 = 39 \, \text{m} | 80 + 400 \, \text{m} |
| C \rightarrow B = 19\cdot2 = 38 \, \text{m} | 79 + 400 \, \text{m} | ||
| D \rightarrow D = 4 \, \text{m} | D \rightarrow A = 19\cdot2 = 38 \, \text{m} | 80 + 400 \, \text{m} | |
| D \rightarrow B = 18\cdot2+1 = 37 \, \text{m} | 79 + 400 \, \text{m} | ||
| B \rightarrow C = 38 \, \text{m} | C \rightarrow C = 4 \, \text{m} | C \rightarrow A = 18\cdot2+3 = 39 \, \text{m} | 81 + 400 \, \text{m} |
| C \rightarrow B = 19\cdot2 = 38 \, \text{m} | 80 + 400 \, \text{m} | ||
| C \rightarrow D = 1 \, \text{m} | D \rightarrow A = 19\cdot2 = 38 \, \text{m} | 77 + 400 \, \text{m} | |
| D \rightarrow B = 18\cdot2+1 = 37 \, \text{m} | 76 + 400 \, \text{m} | ||
| B \rightarrow D = 39 \, \text{m} | D \rightarrow C = 3 \, \text{m} | C \rightarrow A = 18\cdot2+3 = 39 \, \text{m} | 81 + 400 \, \text{m} |
| C \rightarrow B = 19\cdot2 = 38 \, \text{m} | 80 + 400 \, \text{m} | ||
| D \rightarrow D = 4 \, \text{m} | D \rightarrow A = 19\cdot2 = 38 \, \text{m} | 81 + 400 \, \text{m} | |
| D \rightarrow B = 18\cdot2+1 = 37 \, \text{m} | 80 + 400 \, \text{m} |
Keď sa pozrieme do tabuľky, vidíme práve 6 rozdielnych súčtov. Konkrétne 475 \, \text{m},\, 476 \, \text{m},\, 477 \, \text{m},\, 479 \, \text{m},\, 480 \, \text{m} a 481 \, \text{m} čo sú všetky možné dĺžky Lychondražovej cesty.
Komentár
Ahojte, príklad bol na štvrtú úlohu vcelku náročný. Väčšina z vás sa s ním odvážne popasovala a často si aj všimla niektoré dôležité pozorovania, napriek tomu vaším riešeniam chýbalo lepšie odôvodnenie, poprípade vám ušla nejaká cesta. Hlavne si treba uvedomiť, že možných ciest z pravého dolného rohu do ľavého je veľa. Ak nejakú nájdete, treba zistiť a ukázať, že žiadna cesta nemá inú dĺžku, pri tom si poprípade viete uvedomiť, že ste si dáku dĺžku nevšimli.Ako vedúci sme trochu zazmätkovali a v zadaní nebolo napísané, ako funguje pohyb v pravej dolnej miestnosti. Keď sa nám stanú takéto veci, často to riešime neskôr v komentároch, tak je cool, keď sa na ne občas pozriete. Nech potom nemáte zbytočnú prácu. Poprípade ak sú nejasnosti, pokojne sa pýtajte.
5. príklad
Ak sa nejaký čas budeme hrať s tehlami zo zadania a nejako natierať vyznačné miesta maltou, možno si všimneme, že keď natrieme napríklad červené miesto čarovnou maltou tak sa nám vždy zníži sila na spodnej tehle o 1. A môžeme overiť, že to platí bez ohľadu na to, ktoré iné miesta sú natreté. Podobne to bude fungovať aj pre zvyšné miesta, keďže v každom riadku sa nám sily iba nejak sčítavajú a rôzne miesta pre maltu sa nám nijak nebudú ovplyvňovať.
Skúsime si teraz natrieť celú vrstvu čarovnou maltou, vtedy bude sila na spodnej tehle 0, a potom nenatrieme vždy iba jedno miesto. Získame tým na spodnej tehle práve tú silu, ktorou prispieva toto miesto. Konkrétne to bude:
| Červené miesto | Oranžové miesto | Žlté miesto | Zelené miesto | Tyrkysové miesto | Modré miesto | Fialové miesto | Ružové miesto |
| 1 | 4 | 12 | 18 | 18 | 12 | 4 | 1 |
Keď už poznáme, ktoré miesto má aký vplyv na spodnú tehlu, pokúsime sa z týchto síl poskladať hodnoty zo zadania. Vždy pôjdeme od najväčšej sily a skúsime si rozmyslieť, či ju máme použiť raz, dvakrát alebo vôbec.
Sila 15
V tomto prípade silu 18 nemôžeme použiť, lebo už samotná je väčšia ako 15.
Sily 12 nemôžeme použiť dve, lebo by sme dostali 24 - číslo väčšie ako 15. Aspoň jednu ale použiť musíme, lebo ak by sme mohli použiť iba sily 1 a 4, hoc aj obe dvakrát, tak dostaneme najviac silu 1+4+4+1=10.
K použitej sile 12 ešte musíme pridať silu 3 (15-12=3). To ale nevieme získať zo zvyšných Síl (1, 4, 4, 1) lebo sila 4 je už samotná väčšia ako 3 a dve jednotky na ňu nestačia.
Preto silu 15 na spodnej tehle dostať nevieme.
Sila 35
V tomto prípade nemôžeme silu 18 použiť 2-krát lebo by sme dostali 36, číslo väčšie ako 35. Ale aspoň jednu použiť musíme, lebo ak by sme použili iba sily 1, 4 a 12, nech aj všetky 2-krát, tak dostaneme silu najviac 1+4+12+12+4+1=34.
Ďalej silu 12 nemôžeme použiť 2-krát lebo by sme dostali 12+12+18=42 čo je väčšie ako 35. Aspoň jednu ale použiť musíme, lebo ak použijeme k sile 18 iba sily 1 a 4 tak vieme dostať najviac 1+4+18+4+1=28.
Už vieme že musíme použiť práve jednu silu 18 a práve jednu silu 12, teda nám do 35 chýba 35-12-18=5. Silu 5 vieme zo síl 1 a 4 poskladať iba jedným spôsobom a to 1+4.
Zistili sme teda, že na dosiahnutie sily 35 musíme použiť každú hodnotu sily práve raz.
Koľkými spôsobmi to vieme dosiahnuť? Ako vieme z tabuľky, pre každú silu ktorú použijeme sú dve miesta, z ktorých ju môžeme dostať, ak ich nenatrieme. Vždy si z nich jedno musíme vybrať, teda máme 4 sily a pre každú 2 možnosti, dokopy 2 \cdot 2 \cdot 2 \cdot 2=\mathbf{16} rôznych kombinácií.
Odpoveď: Na spodnej tehle nevieme získať silu 15 a silu 35 vieme získať 16 spôsobmi.
Komentár
Niektoré riešenia sa pokúšali si inými spôsobmi vyjadriť spodné políčko, napríklad najprv zistiť možnosti v tehlách na riadku pod maltou, čo bolo väčšinou náročnejšie doviesť do bezchybného konca. Väčšina z vás ale zvládla zistiť nemenné sily ktorými prispievajú jednotlivé miesta k spodnej tehle. Často to ale nestačilo na plný počet bodov, pretože veľa riešiteľov nedostatočne vylúčilo všetky možnosti, ako by sme z nich mohli vyskladať 15 alebo 35 inak ako správnym spôsobom.
Bodovanie
Vo väčšine prípadov sme udeľovali 3 body za vyrátanie toho, ako každé miesto ovplyvňuje spodnú tehlu, potom 2 body za dôkaz že silu 15 nevieme dosiahnuť a 5 bodov za dôkaz že sa dá 35 poskladať iba z 1+4+12+18 a výpočet počtu riešení.
6. príklad
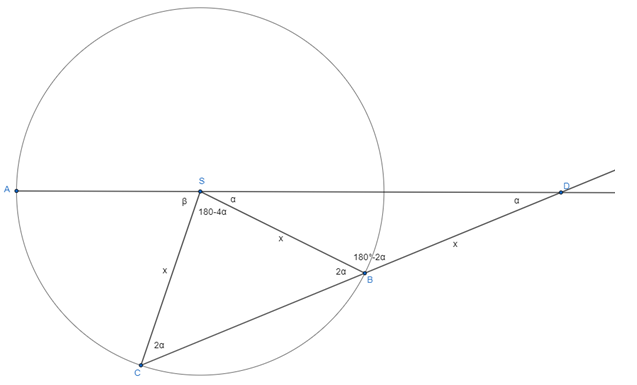
Označíme si \measuredangle SDB ako \alpha a \measuredangle ASC ako \beta. Vieme, že úsečky SC a SB sú obe polomerom kružnice a taktiež zo zadania vieme, že úsečka SC je rovnako dlhá ako úsečka BD. To znamená, že |SC|=|SB|=|BD|=x.
Keďže je \triangle SDB rovnoramenný, tak \measuredangle SDB a \measuredangle BSD sú zhodné. Súčet vnútorných uhlov v trojuholníku je 180°, v \triangle SDB bude teda \measuredangle DBS=180°- \measuredangle SDB- \measuredangle BSD a keď namiesto zhodných uhlov \measuredangle SDB a \measuredangle BSD dosadíme \alpha, tak dostaneme \measuredangle DBS=180°-2\alpha.
Vieme, že \measuredangle SBC a \measuredangle DBS sú susedné uhly a teda platí:
\measuredangle SBC+\measuredangle DBS=180°
\measuredangle SBC+180°-2\alpha=180°
\measuredangle SBC=2\alpha
Keďže je \triangle SBC rovnoramenný, tak \measuredangle SBC a \measuredangle BCS sú zhodné, čiže \measuredangle BCS=2\alpha. Súčet vnútorných uhlov v trojuholníku je 180°, teda \measuredangle CSB=180°-4\alpha
Vieme, že \measuredangle ASD=180°, potom tiež platí:
\alpha+\beta+\measuredangle CSB=180°
\measuredangle CSB=180°-\alpha-\beta
Našli sme dve možnosti na vyjadrenie \measuredangle CSB, dáme si ich teda do rovnosti.
180°-\alpha-\beta=180°-4\alpha
-\alpha-\beta=-4\alpha
\beta=3\alpha
Odpoveď: Pomer veľkosti \measuredangle ASC a \measuredangle SDB je 3:1.
Komentár
V tomto príklade existovali dve možné polohy bodu A. Jedna ako v našom riešení, kde bod S leží medzi A a D, druhá ako na obrázku nižšie, kde A leží medzi S a D.
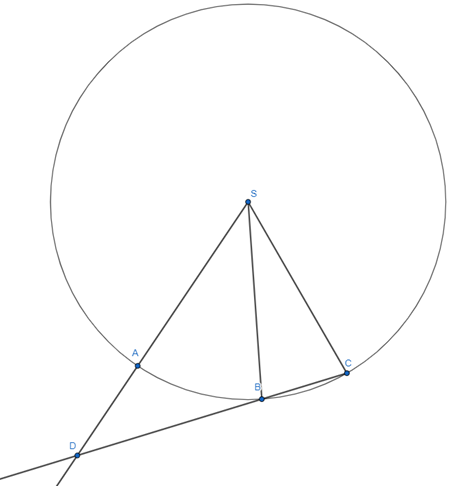
Príklad sa aj v takomto prípade riešil rovnako, líšilo by sa len jedno vyjadrenie \measuredangle CSB, ktoré by vyšlo \beta - \alpha namiesto 180° - \alpha - \beta a samozrejme výsledok (\beta = 180° - 3\alpha), ktorý by sa nedal vyjadriť ako pomer.
Úplne správne riešenie by malo obsahovať obe možnosti, keďže sa však postup nelíšil, body sme nestrhávali, ak ste poslali len jednu z nich. Najmä vo vyšších kategóriách matematickej olympiády si na to však treba dávať pozor.
7. príklad
Najprv sa pozrieme na deliteľnosť dvoma. Všimnime si, že každé prvočíslo okrem 2 je nepárne.
Ak by sklad D alebo vrchné poschodie V bolo párne číslo, teda 2, tak stred S medzi 2 a 419 by nebolo celé číslo (lebo S=(419+2)/2). Čo znamená, že sklad ani vrchné poschodie nemôže byť 2.
Už vieme, že aj sklad aj vrchné poschodie sú nepárne čísla. Vieme, že aj S musí byť prvočíslo, čo znamená, že bude nepárne. Ak by nebolo, znamenalo by to, že sklad by bol menší ako toto párne prvočíslo. My však vieme, že jediné párne prvočíslo 2 je zároveň najmenšie prvočíslo. Keďže D je prvočíslo tak S musí byť nepárne.
Oznamče R = V-S = S-D, keďže S je stred medzi skladom a vrchný poschodím. Všimnime si, že R musí byť párne lebo V,S,D sú všetko nepárne čísla.
Prejdime na zvyšky po delení tromi. Zo zadania vieme, že R nie je deliteľné 6. Keďže sme už ukázali, že je R párne stačí nám riešiť už iba deliteľnosť 3. Číslo R môže mať po delení 3 tri rôzne zvyšky, a to 0,1,2. Teraz rozoberiem tieto prípady osobitne.
Zvyšok 0
Ako sme už zistili, R nemôže byť deliteľné 3, inak by bolo deliteľné aj 6, čo zadanie vylučuje. Preto R nemôže mať zvyšok 0.
Zvyšky 1 a 2
Ukážeme, že ak R má zvyšok 1 alebo 2 tak jedno z čísel D,S,V musí byť 3.
Nebude to vôbec ťažké. Ukážeme, že čísla V,S,D budú mať každé iný zvyšok po delení 3. Keďže zvyšky sú len tri a aj čísla sú tiež práve tri, jedno z nich bude musieť mať zvyšok 0, a teda byť deliteľné 3.
Pôjdeme na to sporom. Predpokladajme, že nejaké dve z čísel V,S,D majú rovnaký zvyšok po delení 3. Ak by rovnaký zvyšok malo V a S alebo S a V muselo by R byť deliteľné 3, čo sme už vyvrátili. Ostáva nám preveriť už len jediný prípad, a to, že V a D by mali rovaký zvyšok. Platí V-D = 2R a teda opäť by R muselo byť deliteľné 3, čo neplatí.
Ukázali sme, že jedno z čísel V,S,D má po delení 3 zvyšok 0 a teda je to násobkom čísla 3. Číslo 419 nie je násobkom 3 a my vieme, že jediné prvočíslo deliteľné 3 je práve samotná trojka. Takže jedno z čísel V,S,D je 3.
Záver
Prešli sme cez všetky zvyšky a dospeli sme k tomu, že jediná možnosť ako to môže platiť je, že jedno čísel V,S,D bude 3. Už vieme, že ani jedno z daných čísel nie je párne. Zároveň 3 je najmenšie nepárne prvočíslo. To znamená, že jediná možnosť je, že najmenšie z čisel V,S,D je 3. Keďže V>S>D lebo R \neq 0
Túto jedinú možnosť už ľahko overíme. Vieme, že D = 3 a tým pádom V = 419. Odtiaľ S = (D+V)/2 = 211 čo je prvočíslo. Tým pádom sme našli jedinú možnosť a to, že ďalšie dve prvočísla sú 3 a 211.
Komentár
Veľká časť z vás urobila tú chybu, že ste neuvažovali s možnosťou, že 419 môže byť aj sklad. To vás nalákalo vyskúšať relatívne malý počet možností a dospieť k výsledku. To však bola veľmi zjednodušená verzia tohto príkladu, a teda sme nemohli udeľovať plný počet bodov. Je však možné, že zo zadania to nebolo úplne zjavné. Preto sa nabúduce neváhajte pozrieť alebo spýtať do komentárov k zadaniu, kde padla presne takáto otázka. Tak isto veľa z vás postavilo svoje riešenie len na skúšaní možností. V príkladoch v Rieškach toto väčšinou nie je cesta a existuje oveľa krajšie riešenie.
8. príklad
Pre prehľadnosť si tu uvedieme, koľko by nás stálo ubytovanie salamadrov a molochov v jednotlivých krboch:
| T | K | V | |
|---|---|---|---|
| S | 80 | 60 | 100 |
| M | 100 | 120 | 80 |
Najprv si predstavíme, že by sme nemali žiadnych salamandrov, ale len 60 molochov. Potom by sme zaplnili všetky tri krby len nimi a spolu by sme za ubytovanie zaplatili 6060 peňazí. Pretože:
100\cdot 15 + 120\cdot 24 +80\cdot 21=6060
Teraz musíme 25 z týchto molochov nahradiť salamandrami. Pozrieme sa na rozdiely cien za ubytovanie magmatických molochov a spopoľňujúcich salamandrov v jednotlivých krboch.
- V tieňovom krbe je cena pre salamandrov 80 peňazí a pre molochov 100 peňazí. Teda tento krb je pre salamandrov o 20 peňazí lacnejší ako pre molochov.
- V kamennom krbe je cena pre salamandrov 60 peňazí a pre molochov 120 peňazí. Teda tento krb je pre salamandrov o 60 peňazí lacnejší ako pre molochov.
- Vo vulkanickom krbe je cena pre salamandrov 100 peňazí a pre molochov 80 peňazí. Teda tento krb je pre salamandrov o 20 peňazí drahší ako pre molochov.
Teda vidíme, že umiestnením čo najvyššieho počtu salamandrov do kamenného krbu, ktorý je pre molochov najdrahší a salamandrov najlacnejší, určite dosiahneme rapídne zníženie ceny. Pokiaľ by sme takto vymenili všetkých molochov v kamennom krbe za salamandrov, tak nám z našich 25 salamandrov ešte stále jeden ostane. Tohoto posledného salamandra sa nám neoplatí dávať do vulkanického krbu, ktorý je najlacnejší pre molochov, ale do tieňového, ktorý je až druhou najlacnejšou voľbou pre obe príšery.
| T | K | V | |
|---|---|---|---|
| S | 1 | 24 | 0 |
| M | 14 | 0 | 21 |
6060-(24\cdot 60)-(1\cdot 20)=4600
Čo sa tiež dá vypočítať ako:1\cdot 80 + 14\cdot 100 + 24\cdot 60 + 0\cdot 120 + 0\cdot 100 + 21\cdot 80 = 4600
Je to ale naozaj najlepšie rozdelenie? Uvedomme si, že takto sme ubytovali najväčší možný počet príšer do ich najlacnejšieho krbu a tie čo nám zvýšili, išli do hneď druhej najlacnejšej varianty pre oba typy príšer, takže nemáme už kde ušetriť. Anku môže stáť ubytovanie všetkých príšer najmenej 4600 peňazí.
Komentár
Veľká väčšina z vás zvládla túto úlohu bez problémov. Najčastejšími chybami bolo, že ste sa pri výpočte výslednej ceny ubytovania buď pomýlili alebo ste ju dokonca vôbec nevypočítali. To boli, samozrejme, zbytočne stratené bodíky z nepozornosti a preto opäť odporúčame vždy si výpočet pre istotu znova skontrolovať a pozorne si prečítať, na čo sa v zadaní pýtame.
9. príklad
Najprv si na obrázku vyznačíme uhly. Môžeme si všimnúť, že keď obrázok otáčame o 90 stupňov a preklápame, zostáva rovnaký. To znamená, že všetky modré a všetky zelené uhly na obrázku sú rovnaké.

Obsah hviezdy vieme vypočítať tak, že od obsahu celého štvorca odčítame obsah tých 8 nevyfarbených trojuholníkov. Pozrime sa na jeden z nich, označený AEX.

Trojuholníky AEX a BHA majú oba jeden zelený a jeden modrý uhol, čo znamená, že sú podobné. Tretí uhol teda tiež majú rovnaký, čiže uhol AXE je pravý. Vďaka tomu tiež vieme, že tieto trojuholníky majú rovnaký pomer strán, teda \frac{|AX|}{|XE|}=\frac{|AB|}{|AH|}. Dosadíme dĺžky ktoré poznáme, |AB|=1\,\text{m} a |AH|=\frac{1}{2}\,\text{m}, z čoho po úprave dostávame |AX|=2|XE|. Označme dĺžku |XE|=x, potom |AX|=2x. Teraz použijeme pytagorovu vetu v trojuholníku AEX a vyjadríme x:
x^2+(2x)^2=|AE|^2 \\ 5x^2=|AE|^2 \\ x=\sqrt{\dfrac{|AE|^2}{5}}=\dfrac{|AE|}{\sqrt{5}}
Dosadíme hodnotu |AE|=\frac{1}{2}\,\text{m}, ktorú poznáme a dostávame:
x = \dfrac{1}{2\sqrt{5}} \, \text{m}
Obsah pravouhlého trojuholníka už vieme zrátať jednoducho ako
S=\dfrac{|AX|\cdot |XE|}{2}=\dfrac{x\cdot(2x)}{2}=x^2=(\dfrac{1}{2\sqrt{5}})^2=\dfrac{1}{20} \, \text{m}^2.
Obsah celého štvorca je 1\text{m}^2 a máme tam 8 trojuholníkov, ktoré musíme odčítať. Obsah hviezdy je teda
1\,\text{m}^2-8\cdot \frac{1}{20}\,\text{m}^2=\frac{20-8}{20}\,\text{m}^2=\frac{12}{20}\,\text{m}^2=\frac{3}{5}\,\text{m}^2.
Odpoveď: Obsah hviezdy je teda \frac{3}{5}\text{m}^2.
10. príklad
Najskôr popíšeme, ako má AnkaP hrať, aby čo najskôr vyhrala, a potom vysvetlíme, prečo to funguje a prečo je to optimálna stratégia.
- AnkaP začína hru umiestnením pyramídy. Keďže na rovine ešte nič nie je, je jedno kam ju umiestni.
- Ľudstvo niekam umiestni svojich n miest.
- V každom ďalšom ťahu AnkaP umiestni svoju pyramídu tak, aby vytvorila čo najviac tzv. potenciálnych trojuholníkov – každá dvojica pyramíd tvorí úsečku, ku ktorej existujú dva body také, že ak na jeden z nich v nasledujúcom kole AnkaP položí pyramídu, vytvoria rovnostranný trojuholník a AnkaP vyhrá.
- Ľudstvo teraz musí pokryť všetky potenciálne trojuholníky mestami, inak AnkaP v nasledujúcom kole vyhrá.
- Ak AnkaP môže vytvoriť rovnostranný trojuholník a vyhrať, urobí to, inak pokračuje krokom 3.
Vieme, že keď AnkaP vyhrá tým, že využije nejaký potenciálny trojuholník vytvorený v predchádzajúcich kolách. Ľudstvo sa však tieto potenciálne trojuholníky bude snažiť zablokovať. Ak teda chce AnkaP vyhrať, musí vyrobiť väčší počet potenciálnych trojuholníkov, než ľudstvo dokáže pokryť.
Vieme, že každá dvojica pyramíd môže vytvoriť najviac dva potenciálne trojuholníky. Najviac teda môžeme zaručiť, aby každá dvojica pyramíd vytvorila dva potenciálne trojuholníky. To spravíme tak, že vždy keď AnkaP položí pyramídu, vytvorí dva potenciálne trojuholníky s každou už položenou pyramídou.
Keď AnkaP pokladá pyramídu, existujú nejaké body, kde ak ju položí, nevytvorí plný počet potenciálnych trojuholníkov – pozrime sa na to, koľko je takýchto bodov:
- Jedna takáto možnosť je položiť pyramídu tak, že nejaký potenciálny trojuholník, ktorý vytvorí, má vrchol v už položenom meste. Každá dvojica pyramídy a mesta tvorí dva takéto body.
- Druhá možnosť je taká, že by pyramída vytvorila dva potenciálne trojuholníky ktoré majú spoločný tretí vrchol. Toto sa stane len, ak AnkaP položí pyramídu do bodu ktorý vytvorí s dvoma už položenými pyramídami rovnoramenný trojuholník s uhlom 120 \degree pri novej pyramíde. Takéto body sú dva pre každú dvojicu už položených pyramíd.
Teda celkovo neoptimálnych bodov je 2 \cdot pyramídy \cdot (pyramídy + mestá). Keďže počet už položených pyramíd aj miest je konečný, ale počet bodov na nekonečnej rovine je nekonečný. Takže vždy bude existovať bod, kam môže AnkaP položiť pyramídu tak, aby vytvorila najväčší možný počet potenciálnych trojuholníkov.
Poďme teraz vyjadriť, koľko ťahov bude AnkeP trvať vyhrať hru pyramídová schéma.
V i-tom ťahu AnkaP položí pyramídu a vytvorí tým dva potenciálne trojuholníky s každou už položenou pyramídou. Bude ich teda 2 \cdot (i-1). Ak ich ľudstvo v nasledujúcom ťahu nedokáže pokryť, tak AnkaP vo svojom ďalšom ťahu vyhrá. To sa stane ak 2 \cdot (i-1) > n. Po úprave rovnice dostaneme postupne:
i-1 > \frac{n}{2}
i > \frac{n}{2} + 1
Vieme však, že AnkaP vyhrá až v nasledujúcom ťahu t = i + 1. Ťah, v ktorom vyhrá, má najmenšie číslo t ktoré vyhovuje nerovnici t > \frac{n}{2} + 2. Toto si rozoberieme na prípady, kedy n je párne alebo nepárne:
Ak n = 2k, teda n je párne: t > \frac{2k}{2} + 2 = k + 2.
Ak n = 2k+1, teda n je nepárne: t > \frac{2k+1}{2} + 2 = k + 2{,}5.
Keďže k je celé číslo, najmenšie t vyhovujúce nerovnici bude v oboch prípadoch k + 3.
Odpoveď: AnkaP vždy vie vyhrať – vyhrá v ťahu s číslom k + 3, kde k = \frac{n}{2} zaokrúhlené nadol.
Komentár
Väčšina z vás použila správny postup, avšak ste odovzdali riešenie k + 2 alebo prípadne k + 1. Toto sa dialo preto, že aj keď ste došli ku správnej nerovnici, treba si všimnúť, že ťah musí byť väčší ako k + 2 a najmenšie prirodzené číslo väčšie ako k + 2 je k + 3.
Toto tiež poukazuje na dôležitosť skúšok správnosti, a kontrolovania si výsledku čo vám vyjde. Ak si za n dosadíme napríklad 0, tak s riešením k + 2 vám vyjde výsledok 2, avšak vieme, že AnkaP určite nemôže trojuholník vytvoriť predtým čo položí tri pyramídy.
Prémia 1
Štyri najlepšie riešenia ktoré sme dostali mali meno s dĺžkou 47. Tieto riešenia boli takéto: šetyporisedemúväťadesiwaťitújesedetúrimúvänásúť
jašeposedemavätyriťadesinatáťatarajisedevänamať
šetyriposedevamäťadesivataťatarisajedenámasiväť
šejosedemapaväťatyridesinatáťajatarisedemaväťan
Bodovanie
- dĺžka 47 a menej - 6 bodov
- dĺžka 48 až 50 - 5 bodov
- dĺžka 51 - 4 body
- dĺžka 52 až 55 - 3 body
- dĺžka 56 až 64 - 2 body
- dĺžka 65 a viac - 1 bod