Vzorové riešenia 3. kola
1. príklad
ABC
ACB
BAC
BCA
CAB
CBA
Môžeme si všimnúť, že sa v každom stĺpci opakujú stále tie isté čísla, čiže nám každý stĺpec dá rovnaké číslo. Toto číslo bude určite dvojciferné, keďže s trojciferným by to bolo veľa a s jednociferným málo. Takže si ho označíme ako X a Y.
Vieme, že Y musí byť 4, keďže 1554 končí touto číslicou.
X400
0X40
00X4
Na to, aby sa nám to rovnalo 1554 musí platiť X = 1.
Vyšlo nám číslo 14. Ale keďže sa v každom stĺpci nachádzala každá číslica dvakrát, tak musíme 14 vydeliť 2, z čoho nám vyjde 7, čo je súčet ABC.
7 vieme zapísať bez 0 len jedným spôsobom a to 1 + 2 + 4. A najmenšie číslo, ktoré vieme vytvoriť z týchto 3 čísel je 124, čo je hľadaný kód.
Kód od Tonyho skrinky je 124.
2. príklad
Na začiatok si uvedomíme, že môže nastať práve jedna zo 4 možných situácií:
- Miro klame každý z 3 dní, kedy nám tieto výroky povedal
- Miro hovorí pravdu v prvý deň
- Miro hovorí pravdu v druhý deň
- Miro hovorí pravdu v tretí deň
Zoberme si situáciu, kedy Miro klame každý z 3 dní, kedy nám tieto výroky povedal:
Pokiaľ Miro klame každý z týchto dní, tak očividne klame aj v prvý aj v 3 deň. Pokiaľ klame v 1. deň, potom musí v pondelok alebo utorok hovoriť pravdu, aby bol jeho výrok klamstvom. To isté platí aj pre 3.deň, teda musí v stredu alebo piatok hovoriť pravdu, aby bol jeho výrok klamstvom. Všimneme si, že obe podmienky musia platiť naraz, ale vidíme, že platiť môže najviac jedna z nich, pretože pravdu hovorí len v jeden deň. Teda Miro hovorí práve v jeden z týchto dní pravdu.
Teraz si rozoberieme situáciu, že Miro hovorí pravdu v druhý deň:
Jeho výrok je: Dnes je štvrtok, sobota alebo nedeľa. Teda si zapíšeme tri po sebe idúce dni a ukážeme, čo sa pri nich deje:
- Streda-štvrtok-piatok
- Piatok-sobota-nedeľa
- Sobota-nedeľa-pondelok
Všimneme si, že v prvý deň hovorí pravdu, lebo reálne klame v pondelok a utorok a tak hovorí pravdu v dva dni, čo nemôže. Teda sme ukázali, že druhý deň určite bude klamať a teda druhý deň musí nutne byť pondelok, utorok, streda a piatok.
Teraz si zoberieme situáciu, že Miro hovorí pravdu v 3.deň:
Opätovne sa pozrieme sa na to, čo sa pri týchto dňoch opätovne deje:
- Nedeľa-pondelok-utorok - nie je tu žiaden problém
- Pondelok-utorok-streda - v stredu klame, lebo klame len v piatok
- Utorok-streda-štvrtok - v utorok hovorí pravdu a teda hovorí pravdu v dva dni, čo nemôže
- Štvrtok-piatok-sobota - vo štvrtok hovorí pravdu a teda hovorí pravdu v dva dni, čo nemôže
Ako poslednú situáciu si ukážeme, ako by to vyzeralo keby hovoril pravdu v prvý deň:
- Nedeľa-pondelok-utorok - v utorok hovorí pravdu a teda hovorí pravdu v dva dni, čo nemôže
- Pondelok-utorok-streda - v pondelok klame, lebo tvrdí, že klame v pondelok a utorok, ale to nie je pravda, lebo v pondelok hovorí pravdu
- Utorok-streda-štvrtok - v utorok klame, lebo tvrdí, že klame v pondelok a utorok, ale to nie je pravda, lebo v utorok hovorí pravdu
- Štvrtok-piatok-sobota - v sobotu hovorí pravdu, lebo naozaj klame v stredu a piatok a tak hovorí pravdu 2 dni v týždni
3. príklad
Vetu "...naplnila najmenší a stredne veľký pohár až po okraj vodou. Potom preliala vodu z oboch pohárov do najväčšieho a tým zaplnila polovicu jeho objemu..." si vieme zapísať ako m+s=\dfrac{1}{2}v, pretože súčet objemu najmenšieho a stredného pohára je polovica objemu najväčšieho.
Ďalej z vety "...Ela znova naliala do stredne veľkého pohára vodu až po okraj. Z tohto pohára preliala vodu najprv do najmenšieho pohára..." vieme zistiť že v strednom pohári nám ostalo s-m vody.
Ak tento objem prelejeme do najväčšieho pohára (kde už je \dfrac{1}{2}v vody), tak tam bude \dfrac{1}{2}v+(s-m) vody čo sa bude rovnať \dfrac{2}{3}v, keďže po preliatí zvyšku v strednom pohári do veľkého pohára budú vo veľkom pohári zaplnené dve tretiny jeho objemu. Čiže dostaneme rovnicu \dfrac{1}{2}v+(s-m)=\dfrac{2}{3}v.
Túto rovnicu si vieme upraviť na tvar \dfrac{1}{2}v=\dfrac{2}{3}v-(s-m). Potom odstránime zátvorku. \dfrac{1}{2}v=\dfrac{2}{3}v-s+m
Ďalej si spojíme rovnice \dfrac{1}{2}v=\dfrac{2}{3}v-s+m a m+s=\dfrac{1}{2}v do tvaru m+s=\dfrac{2}{3}v-s+m.
Odpočítame m a dostaneme s=\dfrac{2}{3}v-s.
Dáme si s na jednu stranu. 2s=\dfrac{2}{3}v
vynásobíme 3kou na tvar 6s=2v.
Vydelíme 2kou aby sme vyjadrili v. 3s=v. Za s doplníme 6 a dostaneme v=18.
Teraz si doplníme s a v do rovnice m+s=\dfrac{1}{2}v. m+6=\dfrac{1}{2}18
Odpočítame 6 a zjednodušíme aby sme dostali m. m=9-6=3.
Teraz len netreba zabudnúť že objemy sú v decilitroch a máme výsledok.
Najmenší pohár má objem 3 decilitre.
Stredný pohár má objem 6 decilitrov a najväčší pohár má objem 18 decilitrov.
4. príklad
Ak toto totiž platí, musí byť počet cukríkov deliteľný 8 a 9 zároveň. Ak je totiž deliteľný 8, musí platiť pravidlo deliteľnosti ôsmimi - posledné trojčísle počtu cukríkov je deliteľné ôsmimi. Nakoľko celé číslo pozostáva zo zhodných cifier, vieme si posledné trojčíslie zapísať ako 111 * C, kde C je cifra, z ktorej sa bude číslo skladať. Nakoľko 111 nie je deliteľné ôsmimi, cifra C musí byť. Cifra C je teda 8.
Teraz musíme ošetriť, aby počet cukríkov bol deliteľný deviatimi. Pravidlo deliteľnosti deviatimi znie, že číslo je deliteľné deviatimi, pokiaľ jeho ciferný súčet je. Nakoľko nám po predelení počtu cukríkov číslom 8 ostalo číslo pozostávajúce zo samých cifier 1, musí ich počet byť deliteľný deviatimi, čiže násobkom 9.
Načo nám toto bolo dobré? Stále máme dokázať, že počet cukríkov bude rozdeliteľný na 37 zhodných kôpok. Posledný trik je v tom, že platí 3 * 37 = 111 alebo 3003003 * 37 = 111 111 111. Ak mám teda 18-ciferné číslo, miesto 9-ciferného, dostal som ho ako 111 111 111 * 1 000 000 000 + 111 111 111, kde sú očividne oba sčítance deliteľné 111 111 111 a tým pádom 37.
Poznámka: Najnižší počet cukríkov, ktoré mohol Miško dostať je 888 888 888, druhý najnižší je 888 888 888 888 888 888 a každý ďaľší sa skladá iba z prirodzeného násobku 9 cifier 8.
Zistiť toto však nebol cieľ úlohy. Dokázať deliteľnosť 37 ak platia stanovené dve podmienky bol.
5. príklad

Obr. 1: Náčrt Hankinej maľby
- uhlopriečky sú na seba kolmé
- uhlopriečky majú rovnakú dĺžku
- uhlopriečky sa navzájom delia na polovice (rozpoľujú)

Obr. 2: Protipríklady
Analogicky vieme odvodiť presne toto aj o trojuholníkoch ADM, BAN a CBO.
Teraz sa zamerajme na uhol OBN. Je zrejmé, že platí
Z tohto teraz vyplýva, že uhly AMD,\,DPC,\,COB,\,BNA sú vnútornými uhlami štvoruholníka zelených bodov MNOP. Teda už vieme, že tento štvoruholník má všetky vnútorné uhly pravé.
Zároveň už teraz vieme, že platí rovnosť dĺžok úsečiek \left| MN \right| = \left| MA \right| + \left| AN \right| a rovnako tak aj pre zvyšné tri strany pravouholníka MNOP. Teraz vidíme, že každá strana pravouholníka MNOP je dlhá pol uhlopriečky malého plus pol uhlopriečky veľkého štvorca. Tieto rovnaké dĺžky sú označené na obrázku písmenami x,y. Keďže obdĺžnik má protiľahlé strany rovnako dlhé, protiľahlé štvorce musia mať všetky rozmery rovnaké (a teda aj polovicu uhlopriečky).
V tejto chvíli má teda štvoruholník MNOP všetky uhly pravé a všetky strany rovnako dlhé. V tom prípade je to nutne štvorec. Hotovo!
6. príklad
Zo zadania vieme, že:
- Vedúci jedli 5 koláčov (pistáciový nie)
- 10 vedúcich zjedlo 4 až 5 koláčov, pretože: „Zároveň tretina vedúcich ochutnala viac ako tri druhy koláčov.“
- 15 vedúcich zjedlo aspoň 3 koláče. Už ale vieme, že 10 z nich zjedlo viac ako 3. Z toho vyplýva, že zvyšných 15 - 10 = 5 vedúcich zjedlo presne 3 koláče
- ostali nám 15 vedúci, ktorí zjedli 1 až 2 koláče.
Vedúci mohli dokopy maximálne zjesť 15 \cdot 2 + 5 \cdot 3 + 10 \cdot 5 = 95 kusov koláčov.
15 \cdot 2, pretože 15 vedúcich zjedlo 1 až 2 (ak počítame koľko maximálne zjedli, tak počítame s tým, že zjedli 2 koláče).
5 \cdot 3, pretože vieme, že 5 vedúcich zjedlo práve 3 koláče.
10 \cdot 5, pretože vieme, že 10 vedúcich zjedlo 4 alebo 5 koláčov (ak počítame koľko maximálne zjedli, tak počítame s tým, že zjedli 5 koláčov).
Aby zjedli z každého koláča minimálne 20 kusov, tak museli minimálne dokopy zjesť 20 \cdot 5 = 100 kusov. Zistili sme, že dokážu zjesť maximálne 95, čo znamená, že vždy bude aspoň jeden druh koláča, z ktorého zjedli menej ako 20 vedúci.
7. príklad
Odpoveď na otázku v zadaní sa pokúsime zistiť tak, že sa budeme snažiť nájsť konkrétny protipríklad rozdelenia, v ktorom Maxo nedokáže vyhrať stávku. Ak sa nám ho podarí nájsť, tak určite bude záležať na rozdelení plániku. V tom prípade nám stačí ukázať, že existuje také rozdelenie plánu, pre ktoré nemôže byť Kubova podmienka splnená.
Predstavme si plánik, v ktorom je 9 menších častí umiestnených v kruhu tak, že sa dotýkajú iba poslednej desiatej časti. To znamená, že sa nachádzajú vo vnútri desiatej časti, tak ako na obrázku 1. Desiata časť sa teda dotýka všetkých zvyšných deviatich častí. Všimnime si, že žiadne tri časti sa všetky medzi sebou navzájom nedotýkajú. Preskúmajme, v ktorej časti môžu na konci skončiť všetky cukríky. Keďže plán je symetrický, stačí sa pozrieť na ľubovoľnú z deviatich vnorených častí a plus na desiatu centrálnu časť.
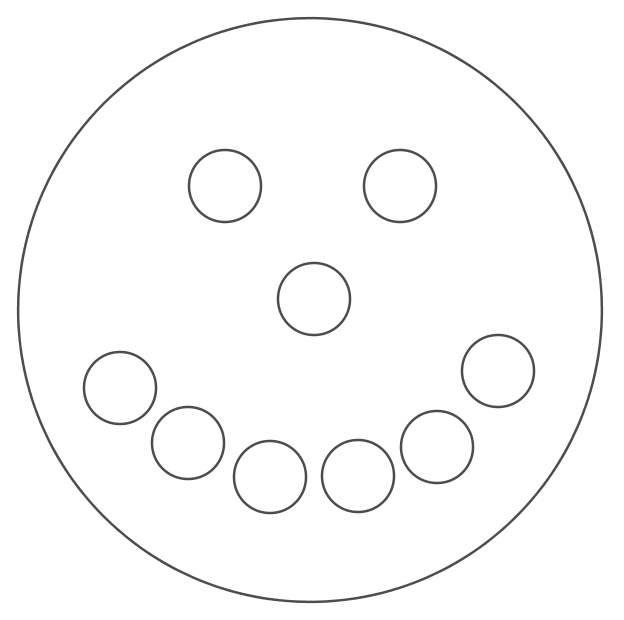
Ak by sme sa rozhodli zhromaždiť cukríky na centrálnej časti, 9 cukríkov tam už máme od začiatku. Zvyšných 81 cukríkov tam musíme postupne v jednotlivých ťahoch popresúvať. Keďže centrálna časť susedí so všetkými zvyšnými časťami plánika, každý cukrík tam dokážeme dostať na jeden ťah. To znamená, že potrebujeme najmenej 81 ťahov na to, aby sme tam z jednotlivých deviatich zvyšných častí presunuli všetky cukríky.
V druhom prípade zhromažďujeme cukríky v jednej z vnorených častí. Prvých 9 cukríkov sa už v danej časti nachádza. Ďalších 9 je hneď vo vedľajšej centrálnej časti a každý z nich vieme dostať do zvolenej cieľovej časti na jeden ťah. Okrem nich je v zvyšných ôsmich vnorených častiach po 9 cukríkov, ktoré najskôr musíme po jednom presunúť do centrálnej časti a až následne do nami zvolenej časti, v ktorej sa cukríky zhromažďujú. To znamená, že každý z týchto 8 \cdot 9 = 72 cukríkov budeme presúvať na minimálne dva ťahy. Dokopy teda potrebujeme minimálne 9 \cdot 1 + 72 \cdot 2 = 153 ťahov na to, aby sme presunuli cukríky do zvolenej vnorenej časti.
Všimnime si, že čísla 81 aj 153 sú obe nepárne. Dozvedeli sme sa, že minimálny počet ťahov potrebných na presunutie všetkých cukríkov do ľubovoľnej z desiatich častí bude vždy nepárny. Zároveň však vieme, že Maxo chce umiestniť všetky cukríky do jednej časti na 2020 ťahov, čo je párny počet ťahov. Ako vieme zmeniť počet ťahov potrebných na umiestnenie všetkých cukríkov v jednej časti z nepárneho počtu na párny?
Ak máme určité usporiadanie cukríkov, vieme jeden z cukríkov posúvať istý počet ťahov tak, že nakoniec ho dostaneme do tej istej časti, v ktorej bol na začiatku tohto usporiadania. Cukrík, ktorý presunieme do istej časti, z nej musíme aj dostať naspäť, aby sme nakoniec dostali počiatočné usporiadanie. Z toho vyplýva, že pokiaľ sa v každom bode dotýkajú maximálne dve časti, budeme potrebovať párny počet ťahov. Pre naše rozdelenie plániku to teda vieme spraviť iba na párny počet ťahov.
Preto nedokážeme zmeniť počet ťahov z nepárneho minimálneho počtu ťahov na párny počet tak, aby sme mali všetky cukríky v jednej oblasti. Tým sme ukázali, že pre náš plánik Maxo nedokáže presunúť všetky cukríky do jednej časti na 2020 ťahov. Preto nedokáže, bez ohľadu na rozdelenie plánu, splniť Kubovu podmienku.
Toto je samozrejme len jeden konkrétny protipríklad. Pozorný čitateľ si určite všimol, že existuje množstvo podobných plánikov, na ktorých Maxo nedokáže vyhrať Kubovu stávku. Medzi odovzdanými riešeniami sa často vyskytovalo rozdelenie plániku na desať častí pomocou deviatich paralelných čiar, alebo rozdelenie plániku pomocou sústredných kružníc. Čo majú všetky tieto rozdelenia spoločné? Každý z nich neobsahuje ani jeden bod, v ktorom sa dotýkajú 3 alebo viacej častí. Pokiaľ by sa totiž na plániku vyskytovali 3 navzájom sa dotýkajúce časti, bolo by možné cukrík presunúť postupne medzi takýmito troma časťami na tri ťahy, pričom by sme nakoniec mali cukrík v časti, v ktorej bol na začiatku tohto presunu. To znamená, že by sme týmto spôsobom vedeli zmeniť nepárny celkový počet ťahov na párny. Vtedy by Maxo dokázal docieliť presunutie všetkých cukríkov na 2020 ťahov do jednej časti.
8. príklad
Označme ďalej výšku rovnobežníka na stranu AB ako v a výšku na AB v ABI~v_1 a výšku na CD v CDI~v_2. Platí, že v = v_1 + v_2.

Pozrime sa na obsahy trojuholníkov ABI,\,CDI. Tie vieme vyjadriť ako \frac{1}{2}\cdot av_1 a \frac{1}{2}\cdot av_2. Ich súčet teda bude:
\frac{1}{2}\cdot av_1 + \frac{1}{2}\cdot av_2 = \frac{1}{2}\cdot a\cdot \left(v_1+v_2\right) = \frac{1}{2}\cdot a\cdot v = \frac{1}{2}\cdot S_{ABCD}.
Keďže obsahy trojuholníkov ABI,\,CDI tvoria dokopy polovicu obsahu zadaného rovnobežníka, obsahy BCI,\,DAI budú dokopy tvoriť zvyšnú polovicu obsahu. Platí teda:

Prejdime na trojuholníky ABI a AKI. Výšku v_1 majú spoločnú, ich strany sú a a ax. Obsah AKI teda vyjadríme nasledovne:
Ďalej si vieme všimnúť, že obsah trojuholníka KBI je rozdielom S_{ABI} - S_{AKI}.
S_{ABI} - x\cdot S_{ABI} = \left(1-x\right)\cdot S_{ABI}
Opäť vieme rovnakým spôsobom vyjadriť obsahy S_{LCI} = \left(1-x\right) \cdot S_{BCI},\, S_{MDI} = \left(1-x\right) \cdot S_{CDI},\, S_{NAI} = \left(1-x\right)\cdot S_{DAI}
Vyššie sme ukázali:
Vráťme sa k štvoruholníkom zo zadania. Ich obsahy vieme zapísať pomocou trojuholníkov, na ktoré sú rozdelené nasledovne:
S_{KBLI} = 6 = S_{KBI} + S_{BLI}\\ S_{LCMI} = 8 = S_{LCI} + S_{CMI}\\ S_{MDNI} = 5 = S_{MDI} + S_{DNI}\\ S_{NAKI} =~? = S_{NAI} + S_{AKI}\\
Pozrime sa teraz na súčet obsahov protiľahlých štvrouholníkov s obsahmi 5,\,6.
6 + 5 = \left(S_{KBI} + S_{BLI}\right) + \left(S_{MDI} + S_{DNI}\right) = \left(S_{KBI} + S_{MDI}\right) + \left(S_{BLI} + S_{DNI}\right) =\\ = \left(S_{LCI} + S_{NAI}\right) + \left(S_{AKI} + S_{CMI}\right) = \left(S_{LCI} + S_{CMI}\right) + \left(S_{NAI} + S_{AKI}\right) = 8 + ?
Vidíme teda, že 5 + 6 = 8 + ?, z čoho vypočítame ? = 3.
Obsah posledného švoruholníka je 3.
9. príklad
V našom prípade nás zaujíma súčet čísel od m do n, čo sa dá vyjadriť ako 1...n a 1...(m-1). Vieme, že m je menšie ako n a tak si m-1 môžeme vyjadriť ako n-k, kde k je rovné počtu sčítancov od m do n. Súčet čísel m...n potom vieme vyjadriť ako:
Poďme sa teraz bližšie pozrieť na činitele k a (2n-k+1). Oba musia byť celé čísla a tak si môžeme hľadanie obmedziť na prvočíselný rozklad čísla 40960 a ich vzájomné súčiny. Rozoberieme dve možnosti, keď je k nepárny deliteľ 20480, a keď je párny.
Ak by k bolo párne: Činiteľ (2n-k+1) by musel byť nutne nepárny, pretože dve párne čísla (2n a k) po pričítaní 1 dajú nepárny výsledok. Povedzme teda, že (2n-k+1) je 1 alebo 5, potom k=40960 alebo k=8192. V oboch týchto prípadoch je k príliš vysoké na to aby sa naša postupnosť čísel skladala iba z kladných celých čísel (a teda prirodzených). Po dopočítaní n uvidíme, že sa v oboch postupnostiach vyskytujú aj záporné čísla:
Odpoveď: Úloha má dve riešenia: 20480 = 4094 + 4095 + 4096 + 4097 + 4098 a 20480 = 20480
Komentár: Ak niekto neuviedol druhé z možných riešení, tak sme body nestrhávali, pretože nebolo zo zadania úplne jednoznačné či môže patriť do riešení aj postupnosť jedného čísla. Spôsobov ako vylúčiť párne k je hneď niekoľko, bohužiaľ však veľa z vás to nedotiahlo po nájdení toho jediného zaujímavého riešenia dokonca a teda dostali bodov podstatne menej, keďže to bola náročnejšia a podstatnejšia časť riešenia. Chválime však všetkých čo sa po prvej nájdenej možnosti snažili hľadať nejaké pravidlá platiace pre ostatné čísla, a nebáli sa spísať iba čiastočné riešenie.
Bodovanie: Za komentár k tomu ako ste sa k správnej odpovedi dostali cez nepárne k sa dalo získať podľa úplnosti najviac 4 body, a za dôkaz že iné riešenia, najmä pri párnom k neexistujú sa dalo získať najviac 6 bodov. Bodovanie sa samozrejme mohlo odlišovať pri špeciálnych prípadoch, a niekedy sa môže zdať trochu prísnejšie aj za menšie nedostatky, predsa len je to najťažší príklad kola.
Prémia 1
 Body za úlohu ste dostávali podľa toho, koľko políčok vaše rozloženie zaberalo:
Body za úlohu ste dostávali podľa toho, koľko políčok vaše rozloženie zaberalo:
- 176 - 8 bodov
- menej ako 176 - 7 bodov
- menej ako 174 - 6 bodov
- menej ako 172 - 5 bodov
- menej ako 169 - 4 bodov
- menej ako 167 - 3 bodov
- menej ako 165 - 2 bodov
- menej ako 160 - 1 bodov
- menej ako 150 - 0 bodov