Vzorové riešenia 1. kola
1. príklad
Máme nájsť osem miestny kód v tvare DDMMRRRR, ktorý obsahuje každú cifru práve raz. Keby mohla byť každá cifra všade bolo by to jednoduché, ale máme určité obmedzenia. Poďme si ukázať, kde nemôže byť ktorá cifra. Začnime rokom. Máme na výber z rokov 1950-1954, teda v každom roku sa nachádzajú cifry 1, 5 a 9. Rok 1951 má dve 1, teda sa nedá použiť a rok 1950 má nulu a to má aj každý z letných mesiacov 06, 07 a 08, teda nám ostávajú roky 1952, 1953 a 1954.
Ako sme už spomenuli mesiac zaberá určite cifru 0 a ešte vždy práve jednu z cifier 6, 7 a 8. V dvoch cifrách určených pre deň sa pozrieme na prvú cifru. Tá môže byť len 0, 1, 2 alebo 3, lebo dni sú od 01 po 31. My už sme však použili 0 a pri prvej cifre 3 môže byť druhá len 0 alebo 1, ktoré sme už obe použili, teda prvá cifra z dňa musí byť 2. To znamená, že rok 1952 nemôžeme použiť.
Už sme si povedali všetky obmedzenia pre deň, mesiac aj rok, bezohľadu nato, ktorú kombináciu dňa, mesiaca a roku použijeme. Teraz si už len musíme vypísať, koľko druhých cifier pre deň vieme použiť, pre ktoré roky a mesiace. Celkovo sme použili pre rok cifry 1, 5 a 9 a jednu z cifier 3 a 4, pre mesiac cifru 0 a jednu z cifier 6, 7 alebo 8 a pre prvú cifru dňa 2. Pre druhú cifru z dňa máme na výber zo všetkých 10 cifier okrem tých, čo sme už použili, ktorých je vždy dokopy 7. Máme teda vždy 3 možnosti pre druhú cifru dňa, nezáleží na tom, ktorý mesiac alebo rok použijeme, keďže cifry, ktoré by sme tým využili sú unikátne, čo znamená, že pre každý rok môžeme použiť každý mesiac a opačne a vždy nám ostanú ešte 3 cifry.
Už to len všetko spočítame. Máme vždy 3 možnosti pre deň, 3 možnosti pre mesiac a 2 možnosti pre rok. Teda dokopy 3 \cdot 3 \cdot 2 = 18 možností, čo je menej ako 20.
Ušiakovi sa podarí otvoriť kufor na menej ako 20 pokusov.
2. príklad
Viem že obvod obdĺžnika ABCD sa rovná 2a+2b=130, predelíme to celé 2 a vznikne nám:
a+b=65.
Obvod obdĺžnika AXYD sa rovná 2\cdot \frac{a}{2}+2b=82=a+2b.
Takže máme 2 rovnice o 2 neznámych, ktoré si upravím tak, aby na jednej strane zostalo len a:
82=a+2b \Rightarrow a = 82-2b
65=a+b \Rightarrow a = 65-b
Keďže a=a, tak:
65-b=82-2b
Čo nám po úprave dáva: b=17
Teraz využijem vzorec, ktorý sme si vyššie dokázali a+b=65, do ktorého dosadím b.
a+17=65
Z toho nám vyplýva, že a=48
Rozmery obdĺžnika ABCD sú 48cm a 17cm.
3. príklad
Zadanie nám hovorí, že hľadáme 4-ciferné číslo deliteľné tromi, pričom ak si jeho cifry označíme postupne A, B, C a D, tak čísla AB, AC AD musia byť prvočísla. Môžeme si všimnúť, že všetky tri prvočísla zdieľajú spoločnú prvú cifru. Zadanie nám tiež hovorí, že všetky cifry sú rôzne a preto, ak chceme takéto tri čísla vytvoriť, A musí byť taká cifra, ktorá tvorí desiatku aspoň trom rôznym prvočíslam. Keď si nájdeme zoznam dvojciferných prvočísel, napríklad na OEIS (https://oeis.org/A000040), zistíme, že takéto A môže byť buď 1, 4 alebo 7.
Pre A = 1 existujú prvočísla 11, 13, 17 a 19, ale cifry B, C, D môžu byť len 3, 7 a 9, keďže sa nesmú opakovať. Takéto číslo ale nikdy nebude deliteľné tromi, bez ohľadu na to, ktorá cifra bude priradená na ktorú pozíciu. Ciferný súčet tohoto čísla bude 1+3+7+9=20, čo nie je násobok trojky. Pravidlo delenia tromi nám však hovorí, že číslo je deliteľné tromi len vtedy a práve vtedy, keď je aj jeho ciferný súčet násobkom 3.
To isté si vieme všimnúť aj v prípade, že A = 7. Vtedy nám vzniknú 3 prvočísla iba ak majú cifry B, C a D hodnoty 1, 3 a 7. To však opäť použijeme cifry 1, 3, 7 a 9 s ciferným súčtom 20. V prípade, že A=4 je to však inak. Tam nám vzniknú prvočísla 41, 43, a 47, teda cifry čísla budú 4, 1, 3 a 7, s ciferným súčtom 15. Ten je deliteľný tromi, a teda aj všetky takéto čísla budú deliteľné tromi.
No a koľko je takýchto čísel už zistíme veľmi ľahko; prvá cifra musí byť 4, a potom buď už vieme, že ak usporiadavame 3 cifry do ľubovoľného poradia, tak počet možností je 3 faktoriál, a 3! = 3 \cdot 2 \cdot 1 = 6, alebo si jednoducho napíšeme všetky možnosti. Na prvé miesto z troch ktoré usporiadavame môžeme dať 3 rôzne čísla, na druhé máme vždy už len 2 možnosti, ktoré nám zostali, a na posledné miesto nám zostane už len jedna cifra. Takto opäť dostaneme 3 \cdot 2 = 6 možností, a to sú: 4137, 4173, 4317, 4371, 4713 a 4731.
Odpoveď: Všetkých rôznych čísel, ktoré spĺňajú podmienky je 6.
4. príklad
- Ak \frac{a}{b} je deliteľné číslom c, tak potom je číslo a je deliteľné súčinom b \cdot c, lebo si to vieme napísať ako a = k\cdot b \cdot c kde k je nejaké prirodzené číslo.
- Takto vieme zistiť, že 6, 12, 44 delia číslo vagónu bezo zvyšku. Z toho ale vyplýva, že číslo vagónu musí byť nejaký násobok najmenšieho spoločného násobku týchto čísel, teda čísla 132.
- V tomto momente už stačí vyskúšať len štyri možnosti: 132, 264, 396, 528 a zistili by sme, že 528 je prvé číslo, ktorého polovica dáva zvyšok 5 po delení 7. Výsledné číslo vagóna tak bude 528. Tu len naozaj bolo treba poriadne vypísať všetky možnosti a ukázať, že prvé tri, ktoré sú menšie naozaj nevyhovujú.
5. príklad
Súčet všetkých čísel na papieri si označíme s a vyberieme si dve ľubovoľné čísla z papiera budú to a a b. Potom platí:
2a=s-a
3a=s
a=\frac{s}{3} (1)
2b=s-b
3b=s
b=\frac{s}{3} (2)
\newline
Vidíme, že aj v rovnici (1) aj v rovnici (2) máme na pravej strane \frac{s}{3}. Keďže sa rovnajú práve strany týchto rovníc, tak sa rovnajú aj ich ľavé strany a teda musí platiť, že a=b.
Keďže sme si zobrali dve ľubovoľné čísla a zistili sme, že sa rovnajú, tak sa musia rovnať všetky čísla napísané na papieri.
x=\frac{n \cdot x-x}{2}
2x=n \cdot x-x
3x=n \cdot x \newline
Keďže vieme, že x je celé kladné číslo,
tak ním môžeme vydeliť (lebo sa nerovná 0)
\newline \underline{\underline{n=3}}
6. príklad
Keďže sa s obsahmi štvoruholníkov ráta ťažko, spojíme bod I s vrcholmi rovnobežníka. Tým rozdelíme časti zo zadania na trojuholníky.

Obr. 1: Rozdelenie na trojuholníky
Pozrime sa teraz na dvojicu trojuholníkov, ktorá má spoločnú stranu vedúcu z bodu I do stredu strany rovnobežníka. Spolu tvoria trojuholník, v našom prípade ABI. Rez koláča rozdeľuje stranu AB na dve rovnaké časti. Dvojica trojuholníkov má teda rovnako dlhé základne a. Rovnako výška trojuholníka ABI, označená v, je spoločná pre obe tieto časti. Obsah trojuholníka sa počíta pomocou strany a výšky na ňu ako \dfrac{a\cdot v}{2}. Keďže majú dva naše trojuhlníky rovnaké dané dĺžky, budú mať aj rovnaký obsah. Označíme ho S_1.

Obr. 2: Dvojica trojuholníkov
Rovnakým spôsobom zistíme aj, že trojuholníky BCI,CDI,DAI sú rezom rozdelené na dve časti s rovnakým obsahom. Trojuholník BCI na časti s obsahom S_2, CDI na časti s obsahom S_3 a DAI na časti s obsahom S_4. Vyznačíme teda v obrázku trojuholníky, ktoré majú rovnaký obsah.

Obr. 3: Rovnaké obsahy
Vráťme sa teda k rezom zo zadania. Zamerajme sa vždy na dvojicu častí v protiľahlých rohoch. Vidíme, že takáto dvojica dokopy obsahuje po jednom trojuholníku každého obsahu - S_1,S_2,S_3,S_4. Tieto páry teda majú teda oba rovnaký obsah - S_1+S_2+S_3+S_4. Pri zohľadnení čísel zo zadania dostaneme nasledujúce rovnice:
Obsah Ušiakovho kúsku koláča je 3.
7. príklad
Nazvime si dve čiary spájajúce po štyri krúžky riadky a štyri čiary spájajúce po tri krúžky stĺpce. Taktiež si uvedomme, že súčet čísel 1 až 9 je rovný 45, označme si neznámy súčet na každej čiare ako S a ešte nech cifra na vrchu je x.
Všimnime si, že dva riadky spolu s krúžkom navrchu používajú každý krúžok práve raz. Teda neznámy súčet S vieme zistiť ako S = \frac{45-x}{2}.
Ďalej sa zamerajme na stĺpce. Všetky zasahujú do vrchného políčka, takže ak ho na chvíľu odignorujeme, súčty v stĺpcoch zostanú stále rovnaké. Presnejšie, vzniknú nám štyri dvojice, ktoré musia mať rovnaký súčet. Ak k tomuto rovnakému súčtu teraz pripočítame x, získame opäť súčet na všetkých čiarach. Rovnicou povedané S = \frac{45-x}{4}+x.
Máme teda dve rovnice, ktorých ľavé strany sú náš neznámy spoločný súčet S. To znamená, že aj pravé strany sa musia rovnať, teda S = \frac{45-x}{2} = \frac{45-x}{4}+x.
Všimnime si, že toto je jednoduchá rovnica s jednou neznámou, a tou je neznáma cifra na vrchu pyramídy. Upravujme teda. Začnime vynásobením číslom 4, získame 90-2x = 45-x+4x. Neznámu x osamostatníme na jednej strane 45 = 5x, z čoho je zjavne vidieť, že x = 9.
Ešte sa musíme presvedčiť, že sa to s deviatkou navrchu dá. Zatiaľ sme totiž iba ukázali, že pre žiadne iné číslo sa to nedá. S vedomosťou, že súčet na každej čiare je 18 (čo zistíme napríklad pomocou S = \frac{45-9}{2} = 18) a trochu hrania sa môžeme nájsť napríklad takéto vyplnenie:
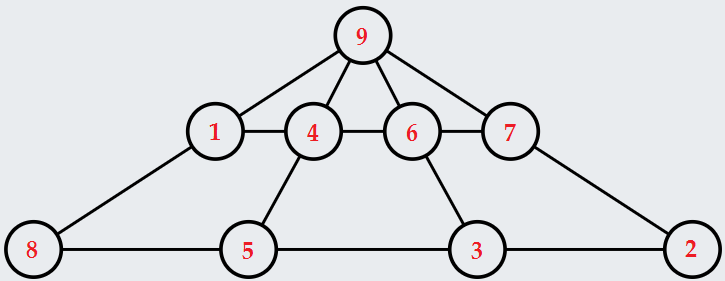
Obr. 1: Príklad vyplnenia všetkých krúžkov
8. príklad
Zhruba jednej polovici riešiteľov sa podarilo príklad správne vyriešiť. Druhá polovica si už tak dobre nepočínala, čo bolo najčastejšie spôsobené neodpovedaním na zadanú úlohu, alebo nepostačujúcim vysvetlením postupu. Preto si najskôr pripomenieme, čo bolo našou úlohou a následne si ukážeme ako postupovať pri riešení.
Zadaný rovnostranný trojuholník, ktorý predstavuje stanicu, má n poschodí zložených z menších trojuholníčkov s dĺžkou strany 1 meter. Našou úlohou je určiť, koľkými spôsobmi môže skupina vedúcich prejsť stanicou na nástupište, teda z vrchného poschodia trojuholníka so stranou dlhou n do stredu spodného ( n -tého) poschodia.
Kľúčové je uvedomiť si, že náš trojuholník má vo všeobecnosti n poschodí, pričom n môže mať hodnotu ľubovoľného prirodzeného čísla (napríklad n = 4 , ale kľudne aj n = 567 poschodí). V zadaní je pre ilustráciu náčrt trojuholníka pre n = 4 . To však neznamená, že ak nájdeme riešenie pre ilustračný obrázok, tak sme vyriešili príklad.
Z toho môžeme intuitívne usúdiť, že naše riešenie bude nejako závisieť od hodnoty n . Ak by sa nám podarilo nájsť vzorec, ktorý by nám po dosadení doň konkrétnej hodnoty n povedal, koľko je pre dané n možných spôsobov, mali by sme v rukách všeobecné riešenie. Presne toto chceme my!
Keď sa nachádzame na určitom poschodí, existuje práve jedna možnosť ako sa na ňom dostať do ľubovoľného trojuholníčka na danom poschodí. Kedže sa nevieme pohnúť na vyššie poschodie, môžeme sa po poschodí posunúť buď doprava alebo doľava. Nemôžeme sa však už vrátiť do trojuholníčka, v ktorom sme boli. Preto pohyb po poschodí je iba jednosmerný, určujúci práve jeden spôsob ako prejsť medzi danými dvoma trojuholníčkami na tom istom poschodí.
Z každého poschodia sa vieme dostať na to nižšie tak, že prejdeme cez jednu zo strán malých trojuholníčkov vedúcu nadol. V k -tom poschodí je takýchto trojuholníčkov práve k . Čiže exisuje k spôsobov ako sa dostať z k -tého poschodia o jedno poschodie nižšie.
Kedže prechody cez jednotlivé poschodie sú nezávislé od prechodov vo vyšších poschodiach, počty spôsobov ako sa dostať na dané poschodie z vrchného poschodia trojuholníka budú súčinom spôsobov prechodov vo vyšších poschodiach.
Z vrchného poschodia vedie k = 1 spôsob prechodu o poschodie nižšie. Preto k -té poschodie má dokopy k! rôznych spôsobov ako prejsť z vrchu trojuholníka na poschodie pod k -tým poschodím.
Na n-té poschodie sa dostaneme z (n - 1) -vého poschodia, preto je (n - 1)! spôsobov ako sa dostať na n -té poschodie. Ako sme si už vysvetlili, na určitom poschodí je len jedna možnosť ako sa dostať do stredného trojuholníčka z ľubovoľného trojuhoľníčka na danom poschodí. Takže zo stanice na nástupište sa vieme dostať 1 \cdot (n - 1)! spôsobmi. Vidíme, že skutočne počet spôsobov závisí od n . Práve sme vyriešili príklad pre všeobecnú hodnotu n .
Odpoveď: Skupina vedúcich môže prejsť stanicou na nástupište (n - 1)! spôsobmi.
9. príklad
Prémia 1
Veľa z vás nepochopilo zadaniu prémie, takže si ho teraz vysvetlíme.
Čiara je spojitá a nedotýkajúca sa samej seba, čo znamená, že ak sa roh štvorca v ktorom je čiara dotýka ďaľšieho štvorca s čiarou, tak je to tou najkratšou cestou.
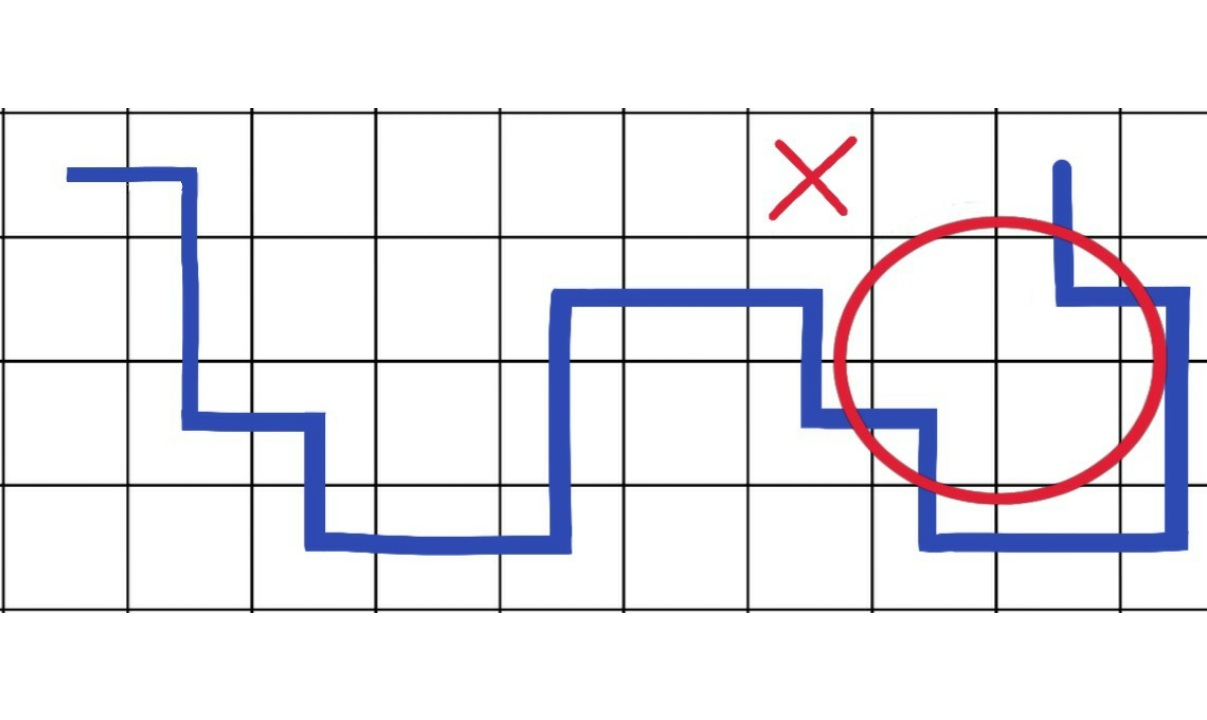
Obr. 1: Dotyk rohom
Navyše to ešte znamená, že ak čiara prechádza dvoma stranou susediacimi políčkami, musí ich priamo spojiť a nemôže ísť medzi nimi cez iné políčka.
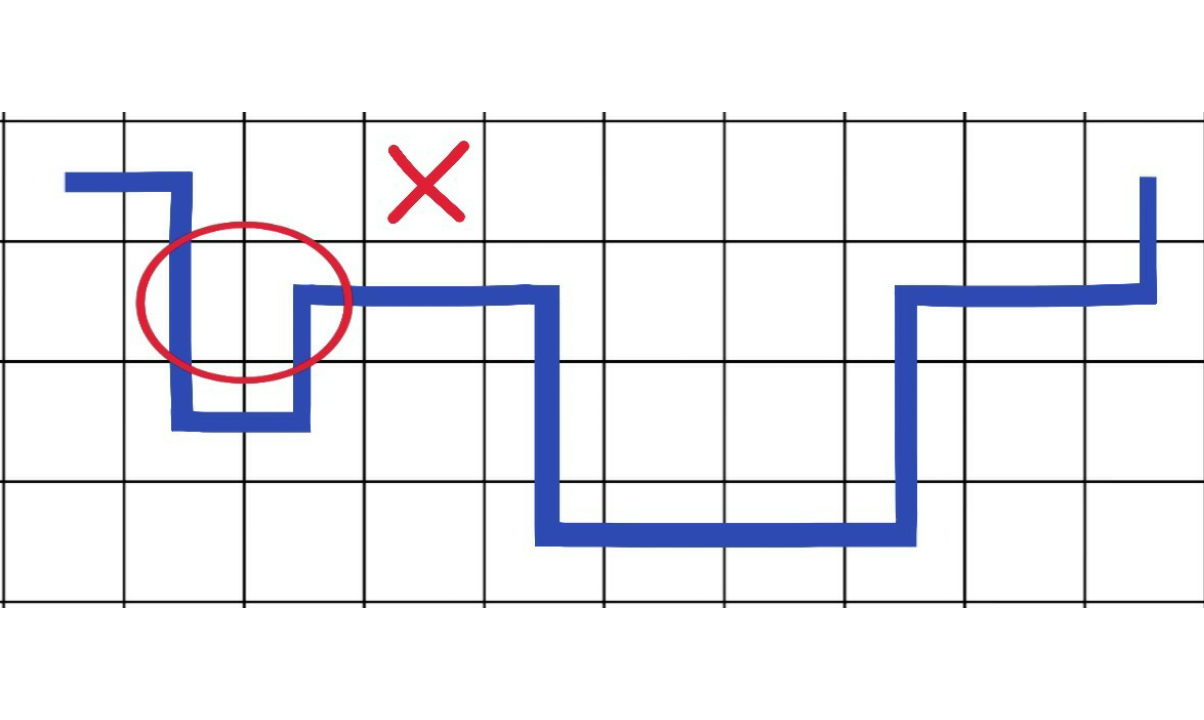
Obr. 2: Dotyk stranou
Keďže tomu veľa z vás neporozumelo, tak sme sa rozhodli, trochu zmeniť hodnotenie. Tí, ktorí to pochopili boli hodnotený od 4 do 7 bodov a tí ktorí nie od 0 do 3. Ak ten, kto zadaniu porozumel, spravil chybu, odrátal sa mu bod.
Najlepšie riešenie malo 124 políčok, na ktorých sa čiara otáčala. Od toho sa odvíjalo aj hodnotenie.
124 políčok = 7 bodov
117-123 políčok = 6 bodov
110-116 políčok = 5 bodov
menej ako 110 políčok = 4 body
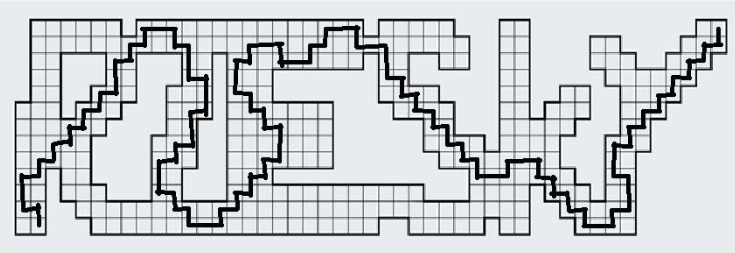
Obr. 3: Najlepšie riešenie