Vzorové riešenia 3. kola
1. príklad
Našou úlohou je nájsť všetky možnosti, aký môže byť súčet všetkých 8 políčok. Keďže biele políčka sú štyri a súčet každej dvojice protiľahlých bielych políčok je 17, súčet všetkých bielych políčok bude 2 \cdot 17 = 34. O každom vyfarbenom políčku vieme, že je súčtom susedných bielych políčok. Z toho vyplýva, že hodnota každého bieleho políčka sa zaráta dvakrát do zafarbených políčok, pretože každé biele políčko susedí s dvomi zafarbenými políčkami. Súčet zafarbených políčok je teda dvojnásobkom súčtu bielych: 2 \cdot 34 = 68. Potom súčet všetkých 8 políčok bude 34 + 68 = 102, čo je jediná možnosť.
Na úlohu sa dá pozerať aj z iného pohľadu. Môžeme si všimnúť, že súčet každej dvojice zafarbených políčok oproti sebe je rovný súčtu všetkých bielych políčok; totiž keď jedno zo zafarbených políčok susedí s určitými 2 bielymi políčkami, zafarbené políčko oproti nemu bude susediť s tými zvyšnými 2 bielymi políčkami, čiže súčet každej dvojice protiľahlých zafarbených políčok bude 34 atď. Toto ale platí len v tejto úlohe, keď máme práve 4 biele a 4 zafarbené políčka, ktoré sa navzájom striedajú po obvode kruhu.
Odpoveď: Existuje jediná možnosť - súčet všetkých 8 políčok je 102 .2. príklad
V reťazci ANANAS-KOKOS-MANGO sa nachádza osem znakov - sedem písmen A, N, S, K, O, M, G a pomlčka. Keďže aj mozgových buniek je osem, tak vieme, že v každej bunke musí byť práve jeden z týchto znakov a každý znak sa bude nachádzať v práve jednej mozgovej bunke, aby sme vedeli vytvoriť daný reťazec.
Na to, aby sme vedeli vytvoriť reťazec ANANAS-KOKOS-MANGO prechádzaním po mozgových bunkách, tak znaky, ktoré spolu susedia v reťazci, sa musia nachádzať v susediacich bunkách, čiže takých, ktoré sú spolu spojené a medzi nimi sa nenachádza žiadna iná bunka. Teraz sa teda pozrieme na každý znak v reťazci a zistíme, aké znaky s ním susedia, čiže aké sú v reťazci tesne pred ním a tesne za ním.
| Susediace s tromi znakmi | Susediace s dvomi znakmi | ||
|---|---|---|---|
| A | N, S, M | N | A, G |
| S | A, -, O | K | -, O |
| - | S, K, M | M | A, - |
| O | K, S, G | G | N, O |
V tabuľke vyššie máme znaky rozdelené do dvoch skupín podľa toho či susedia s tromi inými znakmi v reťazci alebo len s dvomi. V prvom stĺpci každej sekcie je potom konkrétny znak a v druhom stĺpci sú vypísané znaky, s ktorými susedí.
Teraz sa pozrieme na to, aké spojenia majú medzi sebou mozgové bunky. Pre jednoduchosť si ich očíslujeme, tak ako je to na obrázku 1:
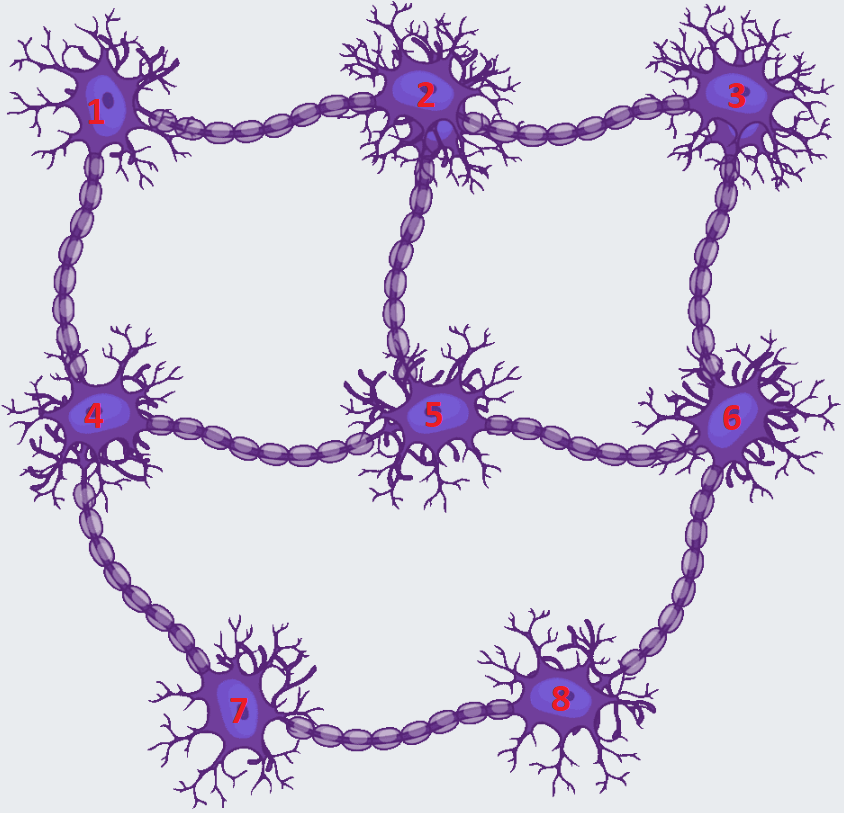
Môžeme si všimnúť, že bunky 1, 3, 7 a 8 sa spájajú priamo len s dvomi inými bunkami a bunky 2, 4, 5 a 6 sa spájajú priamo s tromi inými bunkami. Keďže máme len štyri bunky, ktoré sa spájajú s tromi bunkami, tak v týchto bunkách budú musieť byť tie znaky, ktoré majú susediť s tromi inými znakmi. A potom znaky, ktoré susedia s dvomi inými znakmi budú v bunkách, ktoré sa spájajú s dvomi inými bunkami.
Teraz sa pozrieme bližšie na to, kde sa môžu jednotlivé znaky nachádzať:
Znak S má susediť s tromi znakmi, z ktorých každý susedí s ďalšími tromi znakmi. Jediná bunka, ktorá susedí s tromi inými bunkami a zároveň aj všetci jej susedia susedia s tromi bunkami, je bunka 5. Z toho vyplýva, že znak S musí byť v bunke 5.
Pozrime sa na bunky 7 a 8. Obidve z nich susedia s dvomi bunkami, sú si navzájom susedmi a ešte každá z nich susedí s jednou bunkou, ktorá susedí s tromi bunkami. Jediná dvojica znakov, z ktorých každý znak susedí s dvomi inými znakmi a jeden z týchto susedov je ten druhý znak z tejto dvojice, je dvojica N a G. To znamená, že máme dve možnosti. Buď bude v bunke 7 znak N a v bunke 8 znak G (možnosť A) alebo bude v bunke 7 znak G a v bunke 8 znak N (možnosť B). Ďalej budeme rozoberať tieto dve možnosti:
Možnosť A:
So znakom N susedí okrem znaku G ešte znak A, takže ten bude musieť byť v bunke 4. Podobne so znakom G okrem znaku N susedí ešte znak O, takže ten bude musieť byť v bunke 6. V bunke 5, ktorá susedí aj s bunkou 4 aj s bunkou 6, už máme písmeno S a to aj naozaj susedí so znakmi A a O. Jeho tretím susedom je pomlčka a tú musíme doplniť na posledného nezaplneného suseda bunky 5, čiže pomlčka bude v bunke 2. Zostáva nám už iba doplniť písmená M a K. Obidve susedia s pomlčkou. Túto podmienku spĺňajú obidve voľné bunky (bunka 1 a bunka 3). Znak M susedí ešte so znakom A, ktorý je v bunke 4, čiže znak M musíme doplniť do bunky 1. Znak K susedí okrem pomlčky aj so znakom O, ktorý je v bunke 6 a teda znak K musíme doplniť do bunky 3.
Doplnili sme všetky znaky do mozgových buniek. Teraz si overíme, či naozaj naše doplnenie spĺňa všetky podmienky zo zadania. Reťazec ANANAS-KOKOS-MANGO vieme spraviť nasledovným presunom medzi bunkami (čísla buniek sú oddelené čiarkami): 4,7,4,7,4,5,2,3,6,3,6,5,2,1,4,7,8,6.
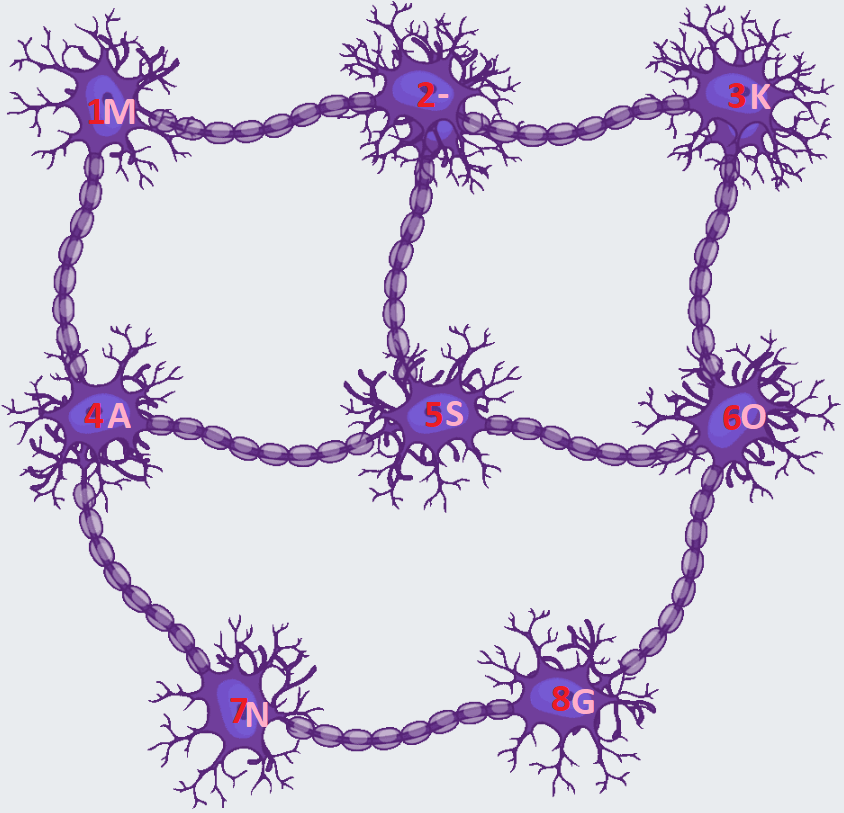
Možnosť B:
So znakom N susedí okrem znaku G ešte znak A, takže ten bude musieť byť v bunke 6. Podobne so znakom G okrem znaku N susedí ešte znak O, takže ten bude musieť byť v bunke 4. V bunke 5, ktorá susedí aj s bunkou 4 aj s bunkou 6, už máme písmeno S a to aj naozaj susedí so znakmi A a O. Jeho tretím susedom je pomlčka a tú musíme doplniť na posledného nezaplneného suseda bunky 5, čiže pomlčka bude v bunke 2. Zostáva nám už iba doplniť písmená M a K. Obidve susedia s pomlčkou. Túto podmienku spĺňajú obidve voľné bunky (bunka 1 a bunka 3). Znak M susedí ešte so znakom A, ktorý je v bunke 6, čiže znak M musíme doplniť do bunky 3. Znak K susedí okrem pomlčky aj so znakom O, ktorý je v bunke 4 a teda znak K musíme doplniť do bunky 1.
Doplnili sme všetky znaky do mozgových buniek. Teraz si overíme, či naozaj naše doplnenie spĺňa všetky podmienky zo zadania. Reťazec ANANAS-KOKOS-MANGO vieme spraviť nasledovným presunom medzi bunkami (čísla buniek sú oddelené čiarkami): 6,8,6,8,6,5,2,1,4,1,4,5,2,3,6,8,7,4.
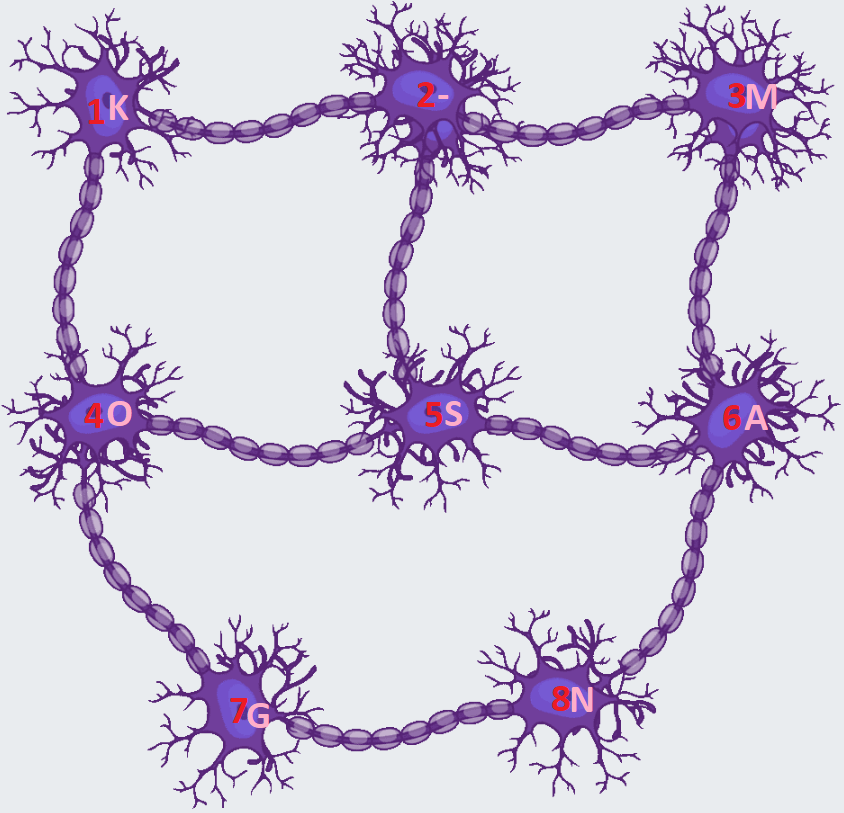
Záver:
Aj v možnosti A aj v možnosti B sme nemali žiadnu možnosť výberu pri doplňovaní znakov do buniek a teda sme našli všetky možnosti ako vieme doplniť znaky do mozgových buniek, aby sme vedeli vytvoriť reťazec ANANAS-KOKOS-MANGO.
Odpoveď: Sú dve možnosti ako vieme doplniť znaky do mozgových buniek tak, aby sme vedeli vytvoriť reťazec ANANAS-KOKOS-MANGO. Sú vyobrazené na obrázkoch pod možnosťou A a možnosťou B.
3. príklad
Riešenie: Najprv sa pozrieme na prvú časť príkladu. Ako prvé je potrebné uvedomiť si, že nás zaujímajú iba jednociferné súčiny cifier, teda keď vynásobíme cifry nejakého čísla tak dostaneme číslo od 0 do 9 vrátane. Dôležitou myšlienkou na začiatok je, že ak máme v ľubovoľnom súčine číslo 0, výsledok tohto súčinu bude 0. Teda keď číslo obsahuje nulovú cifru, je jedno koľko a aké budú ostatné cifry, ciferný súčin bude vždy 0. Potrebujeme nájsť najväčšie číslo také, aby sa jeho cifry neopakovali. Keďže čím má číslo viac cifier, tým je väčšie, chceme aby nami hľadané číslo malo čo najviac cifier. Preto každú cifru použijeme práve raz. Aby bolo číslo čo najväčšie, musia byť čo najväčšie cifry na čo najväčších pozíciach, teda usporiadame cifry od najväčšej po najmenšiu a dostaneme číslo 9876543210. Toto číslo je ale párne, preto musí byť jednotka na mieste jednotiek, teda hľadaným číslom je 9876543201.
Teraz sa presuňme na druhú časť. V tejto časti máme vytvoriť čo najväčšie číslo, ktoré neobsahuje cifru nula a má všetky cifry navzájom rôzne. To znamená, že štyri ani viac cifier mať nemôže, lebo súčin štyroch - aj najmenších cifier je 1 \cdot 2 \cdot 3 \cdot 4 = 24 a teda by to po prvej minúte nevybuchlo. Skúsme teda nájsť nejaké trojciferné číslo.
Toto číslo má byť párne, teda jeho posledná cifra je aspoň 2. To ale znamená, že ak by malo ktorúkoľvek cifru 5 alebo viac, tak by súčin už vyšiel aspoň 10, čo je veľa. Výber cifier sa teda zmenšil na tri cifry z \lbrace 1, 2, 3, 4 \rbrace. Pozrime sa na všetky štyri možné trojice cifier, teda 123, 124, 134, 234. Ciferný súčin sa zmenou poradia nemení. Navyše kombinácie 134 a 234 dávajú dvojciferný súčin cifier. Z možností trojíc 123, 124 vieme vytvoriť šesť párnych čísel, a to presne 132, 312, 124, 142, 214, 412. Z týchto najväčšie je 412 a ako ľahko overíme, že toto číslo naozaj po prvej minúte vybuchne.
Nakoniec tretia časť. Všimnime si, že ak je naše číslo 55, tak máme sled 55 \to 25 \to 10 \to 0. Preto riešenie v tejto časti je NAJVIAC 55. Ešte treba overiť, či náhodou neexistuje riešenie, ktoré je ešte menšie.
Poďme teda od najmenších čísel:- Jednociferné naše číslo zjavne nemôže byť, lebo vybuchuje hneď.
- Čísla 10 až 19 sa po prvej minúte zmenia na svoju cifru jednotiek, pretože platí 1 \cdot c = c.
- Čísla 20 až 24 majú ciferný súčin jednociferné číslo a teda nevyhovujú.
- Ďalej čísla 25 až 29, tie majú ciferný súčin medzi 10 a 19 a teda už v druhej minúte vybuchnú.
- Čísla 30 až 33 majú ciferný súčin jednociferné číslo a teda nevyhovujú.
- Ďalej už iba skúšame:
- 34 \to 12 \to 2 - to je zle, iba 2 minúty
- 35 \to 15 \to 5 - to je zle, iba 2 minúty
- 36 \to 18 \to 8 - to je zle, iba 2 minuty
- 37 \to 21 \to 2 - to je zle, iba 2 minúty
- 38 \to 24 \to 8 - to je zle, iba 2 minúty
- 39 \to 27 \to 14 \to 4 - toto vyhovuje!!
Keďže sme overili všetky menšie čísla, tak 39 je určite najmenšie. Máme teda hotovo.
Odpoveď: Pekne po častiach, správne čísla sú 9876543201, 412, 39.
4. príklad
Vieme, že postupnosť sa skladá z 9 čísiel a práve 5 z nich sú štvorky. To znamená, že 9-5=4 čísla v postupnosti musia byť iné ako 4. Keďže dve po sebe idúce čísla nemôžu byť rovnaké, tak medzi 5 štvorkami musia byť aspoň 4 čísla (lebo medzi 5 štvorkami sú „4 medzery“ a v každej tejto medzere musí byť aspoň jedno číslo). A máme práve 4 čísla iné ako 4 čo znamená, že v každej tejto „medzere“ musí byť jedno číslo iné ako 4. Postupnosť čísiel bude teda v tvare 4A4B4C4D4, pričom pod písmenami A,B,C,D bude jedno z čísiel 1,2,3. Keďže rozmiestnenie štvoriek nemôžeme meniť (neplatilo by pravidlo, že ide vždy na inú stenu), tak štvorky neovplyvňujú počet možných postupností. Rozdiely medzi postupnosťami budú teda len čísla na miestach A,B,C,D.
Vieme, že súčet čísiel celej postupnosti je 30. Súčet štvoriek v postupnosti je 5\cdot4=20. Súčet čísiel A,B,C,D bude teda 30-20=10. Poďme sa teda pozrieť aké čísla sa môžu skrývať pod A,B,C,D:
Menej ako dve trojky medzi číslami nemôžu byť, lebo súčet by bol nanajvýš 3+2+2+2=9.
Keď máme aspoň 2 trojky, tak môžeme vyskúšať akoby vyzerali ďalšie čísla:
- K dvom trojkám pripočítame jednu 1: 3+3+1=7 takže štvrté číslo musí byť 3
- K dvom trojkám pripočítame jednu 2: 3+3+2=8 takže štvrté číslo musí byť 2
- K dvom trojkám pripočítame jednu 3: 3+3+3=9 takže štvrté číslo musí byť 1
Vidíme, že prvá a tretia možnosť je rovnaká, čiže čísla A,B,C,D môžu byť len 3,3,3,1 alebo 3,3,2,2.
Teraz už len potrebujeme zistiť koľkými spôsobmi vieme usporiadať čísla 3,3,3,1 a 3,3,2,2:
Usporiadať čísla 3,3,3,1 môžeme 4 spôsobmi. Je to preto, lebo jednotku môžeme dať na 4 rôzne miesta a na zvyšných by sa museli nachádzať už len trojky.
Čísla 3,3,2,2 vieme usporiadať 6 spôsobmi. Je to preto, lebo prvú dvojku vieme dať na 4 rôzne miesta. Druhú dvojku vieme potom dať na 4-1=3 rôzne miesta, teda 4\cdot3=12 možností. Takto sme však zarátali každú možnosť dvakrát (lebo ak dáme prvú dvojku na 3. miesto a druhú na 1. miesto je to to isté akoby sme dali prvú dvojku na 1. miesto a druhú na 3. miesto). Čiže dvojky vieme rozmiestniť \frac{4\cdot3}2=6 spôsobmi. Ostali nám už len dve trojky a pre ne máme pri každej možnosti iba dve voľné miesta, takže počet možností sa nám nezvýši.
Takto sme zistili, že pre čísla 3,3,3,1 máme 4 možnosti a pre čísla 3,3,2,2 máme 6 možností čo je dokopy 4+6=10. Šálka teda mohol napísať 10 možností.
Komentár:
Väčšina ste mali správny výsledok, lenže nedokázali ste kroky, ako ste sa k tomu výsledku dostali. Viacerí ste poriadne nedokázali prečo 4 čísla, ktoré sú 1, 2 alebo 3 môžu byť len 3, 3, 3, 1 a 3, 3, 2, 2. Keď chcete nájsť všetky možnosti v nejakom príklade, tak vždy musíte napísať do postupu ako ste ich našli (napísať výsledok v Rieškach nestačí).
Hodnotenie:
- 3b za vysvetlenie prečo musí byť postupnosť v tvare 4A4B4C4D4 a uvedomenie si, že štvorky nemôžu byť na iných miestach a že neovplyvňujú počet možností.
- 1b za ukázanie, že čísla iné ako 4 majú súčet 10.
- 4b za dôkaz, že čísla iné ako 4 môžu byť len 3,3,3,1 alebo 3,3,2,2
- 2b za vypočítanie počtu možných rozmiestení čísiel iných ako 4.
5. príklad
Vieme, že nech ide ktorýmkoľvek smerom, tak rovný úsek prejde stále za rovnaký čas. Teda podľa vzorca t=s/v si vieme zistiť, za aký čas sme prešli danú vzdialenosť: t=80\div4=20\,\text{s}. Teraz zistíme, koľko trvalo prejsť len schodiská, teda od časov v zadaní odčítame čas potrebný na prejdenie roviny:
smerom na slobodu: 56\,\text{s}-20\,\text{s}=36\,\text{s}
smerom do hladomorne: 47\,\text{s}-20\,\text{s}=27\,\text{s}
Teraz si podľa vzorca t=s/v zostavme rovnice pre cestu na slobodu a do hladomorne, pričom označme x ako dĺžku schodiska smerom hore v smere von z hladomorne a y ako dĺžku schodiska smerom dole v smere von z hladomorne:
smerom na slobodu: x\div2+y\div5=36\,\text{s}
smerom do hladomorne: x\div5+y\div2=27\,\text{s}
Teda riešme sústavu rovníc zadanú vyššie:
Vynásobíme obe rovnice číslom 10:
Druhú rovnicu vynásobíme -2{,}5:
Rovnice sčítame:
Podelíme obe strany rovnice -10{,}5:
Dosadíme hodnotu y do jednej z rovníc (je jedno do ktorej, keďže by sme mali dostať ten istý výsledok):
Od oboch strán odčítame 6:
Obe strany vynásobíme 2:
Dostávame teda, že x=60\,\text{m} a y=30\,\text{m}, čo sú naše hľadané dĺžky.
6. príklad
Označme si číslo, ktoré si Karin napíše na papier x, potom aj počet posebeidúcich čísel je x. Rozdeľme to teraz na dva prípady, ak x, je nepárne, tak určite existuje v danej postupnosti postupne o jedna sa zväčšujúcich čísel dáke stredné číslo. Toto číslo si pomenujme y. Potom naša postupnosť vyzerá, pre prípad x=5 takto:
y-2;\, y-1;\, y;\, y+1;\, y+2
Už na tomto malom prípade si môžeme všimnúť, že nám tie zvyšky do seba tak pekne zapadajú, somozrejme by sme to chceli zovšeobecniť. Takže od toho stredného čísla, ktoré vždy existuje, nám čísla jedným smerom rastú a druhým smerom klesajú, s tým, že dokopy ich je x, preto práve (x-1)\div2, bude väčších ako to stredné, ktoré je y. Takže dostávame:
y-(x-1)\div2;\, \ldots; y-1;\, y;\, y+1;\, \ldots;\, y+(x-1)\div2
Teraz presne to, čo máme navyše v číslach väčších ako y, nám v tých menších chýba. Vo výsledku teda ich súčet môžeme zrátať ako to stredné, y, krát ich počet. Ten je x, súčet vieme teda vypočítať ako x \cdot y. To je očividne delitelné x. Je teda jasné, že ak na papier Karin napíše ľubovoľné, nepárne číslo, x, tak súčet x čísel v rade bude ním delitelný. Toto má aj peknú geometrickú interpretáciu, kde je vidieť, ako sa tie čísla skladajú do seba:
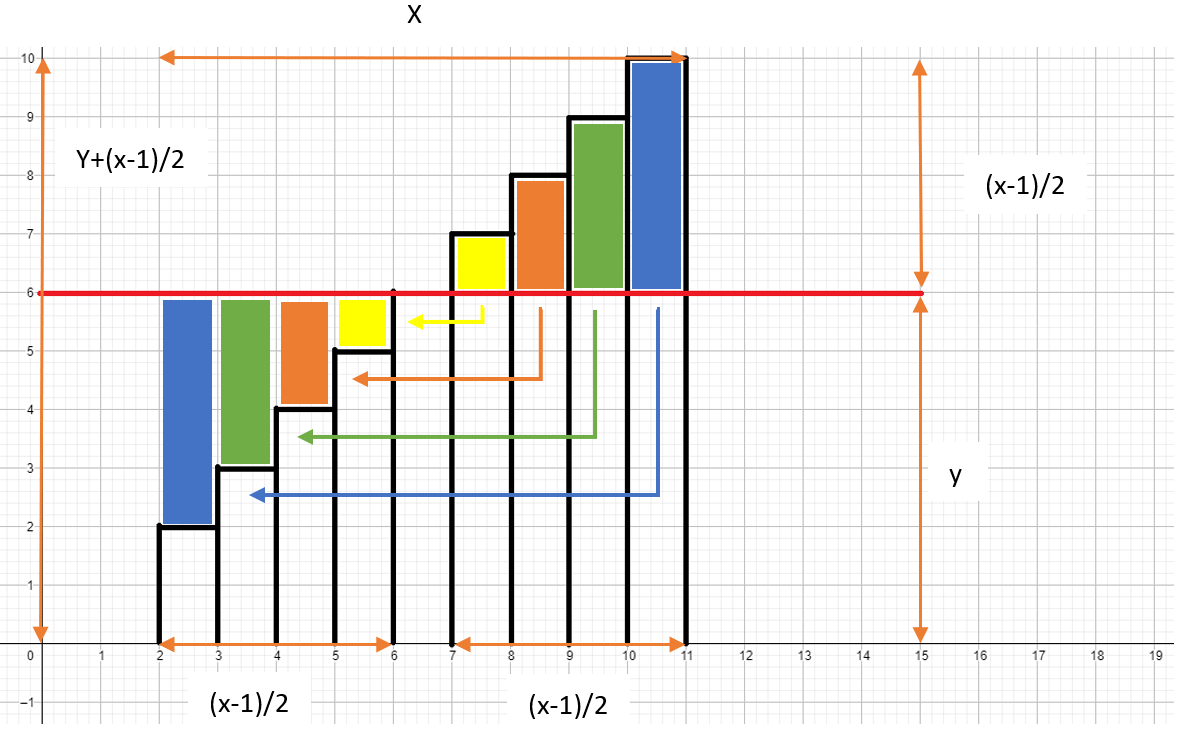 Keď chceme tú postupnosť zrátať, tak vlastne môžeme zrátať obsah obdĺžnika s dĺžkami strán x a y.
Keď chceme tú postupnosť zrátať, tak vlastne môžeme zrátať obsah obdĺžnika s dĺžkami strán x a y.
Pokiaľ Karin na papier napíše párne číslo, tak sa na to vieme pozerať veľmi podobne. Hlavný rozdiel je v tom, že nevieme nájsť toto stredné číslo. Zvoľme si naše nové y, to menšie z dvoch stredných čísel. Naša postupnosť vyzerá potom tak, že každý jej člen, okrem toho najväčšieho má pár, s ktorým dáva súčet y:
y-(x-2)\div2;\, \ldots;\, y-1;\, y;\, y+1;\, \ldots;\, y+(x-2)\div2;\, y+(x-2)\div2+1
Ich súčet vieme vyjadriť ako súčet tých, ktoré do seba po dvoch zapadajú, ktorých je x-1 a k nim prirátame ten posledný člen. Nakoniec celkový súčet bude teda:
(x-1) \cdot y+(y+(x-2)\div2+1)=x \cdot y+x\div2.
Môžeme si všimnúť, že daný súčet teraz nie je deliteľný x, lebo nám ostane y+\frac{1}{2}, čo nie je celé číslo. Preto ak Karin na papier napíše párne číslo x, tak súčet x posebeidúcich čísel nebude deliteľný x. Odporúčam sa aj nad touto druhou časťou zamyslieť aj geometricky.
Komentár: Vo všeobecnosti ste príklad veľmi pekne zvládli. Hlavný problém bol, že mnohí z vás úlohu popísali dosť krátko a často sa nedostatočne venovali dôležitým bodom v riešení.
7. príklad
 Prvé riešenie:
Prvé riešenie:
Osi strán p, q su kolmé na strany trojuholníka BC, CA a zároveň aj na seba, teda strany trojuholníka BC, CA sú na seba kolmé. Trojuholník ABC je teda pravouhlý.
Vieme, že v pravouhlom trojuholníku, sa osi strán pretínajú v strede prepony. Toto vieme ľahko dokázať cez Talesovu kružnicu; to je opísaná kružnica pravouhlého trojuholníka: Bod, v ktorom sa pretínajú osi strán trojuholníka, je stredom opísanej kružnice daného trojuholníka, a stred Talesovej kružnice leží v strede prepony. Tento bod si označíme S.
Bod S je teda stredom strany AB a bod C je vrchol trojuholníka. Ťažnica je úsečka, ktorá spája vrchol trojuholníka so stredom protiľahlej strany, a teda úsečka SC je ťažnica. Tá je navyše delená ťažiskom K v pomere 2:1, teda \left | KC \right | je dva krát dlhšia ako \left | SK \right |. Ťažisko a stred strany máme a teda vieme zistiť kde je vrchol C.
Bod C leží na polpriamke SK , a je vzdialený 3 \cdot \left | SK \right | od bodu S. S, a K sú dané, takže bod C stačí jednoducho skonštruovať.
Priamky p, q sú osi strán BC, CA, teda prechádzajú stredom strán BC, CA a sú na ňe kolmé. To znamená že body A, B, vieme jednoducho skonštruovať. A to tak že spravíme osovú súmernosť bodu C podľa priamok p, q.
Druhé riešenie:Z prvého riešenia použijeme fakt, že výsledný trojuholník je pravouhlý. Pozrime sa teraz ako ďaleko je ťažisko od osi odvesny v pravouhlom trojuholníku.
Vzdialenosť bodu od priamky určujeme ako dĺžku kolmice z daného bodu na priamku. Označme postupne päty kolmice z ťažiska na strany BC, AB ako L, M. Ďalej nech D,E sú postupne stredy strán BC, AB. Vďaka rovnobežnosti vieme povedať, že vzdialenosť ťažiska K od priamok p, q je rovnaká ako dĺžky |DL|, |EM|.
Teraz opäť použijeme, že bod S, ktorí je priesečníkom priamok p, q leží v strede strany AC. Keďže BS je ťažnica a K je ťažisko, tak platí |BK| = 2|KS|. Keď sa pozrieme na kolmý priemet úsečky BS na stranu AB, tak dostaneme úsečku BE. Bod K sa zobrazí na M. Takýto kolmý priemet zachováva pomery dĺžok (vyplýva z podobnosti) a teda platí |BM| = 2|ME|.
Analogicky |BL| = 2|LD|. To znamená, že vieme zostrojiť strany AB, BC tak že nakreslíme rovnobežky s priamkami p, q do dvojnásobnej vzdialenosti od bodu K tak aby sa bod K nachádzal vnútri oboch rovnobežkových pásov. Nakoniec ukončíme riešenie rovnako, iba popreklápame bod B cez priamky p, q aby sme dostali vrcholy A,C.
Komentár:Viacerí z vás nevychádzali zo zadania, toto je v riešeniach veľmi dôležité, lebo sa viete veľmi ľahko popliesť, keď začnete ako sa vám zachce.
Viacerým z vás sa tiež podarilo dokazovať niečo čo ste vôbec nemali. Napríklad ste povedali, že viete narysovať trojuholník a potom nájsť jeho ťažisko. Toto po vás však zadanie nechcelo. V zadaní sa písalo, že ťažisko je už narysované a treba okolo neho narysovať taký trojuholník, aby bod K bol naozaj jeho ťažisko. Nabudúce si prečítajte zadanie aj desaťkrát; hlavne, aby ste sa nepomýlili.
8. príklad
Pre ľubovoľné usporiadanie kľučiek medzi zámkami si môžeme všimnúť, že zámky sú rozdelené do niekoľkých súvislých skupín veľkosti aspoň dva - medzi každými dvoma susednými zámkami v ľubovoľnej takejto skupine je kľučka, no medzi dvoma susednými zámkami z rôznych skupín sa žiadna kľučka nenachádza. To znamená, že tieto skupiny sa navzájom neovplyvňujú, teda ak stlačíme ľubovoľnú kľučku, tak dva zámky, ktoré zmenia svoj stav, budú patriť do tej istej skupiny.
Pokiaľ je v skupine párny počet zámkov, dajú sa jednoducho otvoriť všetky tak, že stlačíme každú druhú kľučku počnúc prvou. Týmto každý zámok prepneme raz, teda otvoríme.
Teraz ukážme, že v skupine s nepárnym počtom zámkov vždy vieme otvoriť najviac všetky zámky okrem jedného. Rovnako ako minule prepnime každú druhú kľučku počnúc prvou. Ostane nám na konci jeden neprepnutý zámok, lebo poslednú kľučku neprepneme.
Pozrime sa na to, ako sa nám môže meniť počet odomknutých zámkov. Keď prepneme ľubovoľnú kľučku, nastane jedna z týchto situácií:- Ak boli zámky pri tejto kľučke oba zamknuté, kľučka ich odomkne a počet odomknutých zámkov sa zvýši o dva
- Ak boli zámky pri tejto kľučke oba odomknuté, kľučka ich zamkne a počet odomknutých zámkov sa zníži o dva
- Ak bol jeden zámok pri tejto kľučke odomknutý a jeden zamknutý, kľučka iba vymení ktorý z nich je zamknutý - počet odomknutých zámkov sa nezmení
Teraz si môžeme všimnúť, že nech sa stane akákoľvek z týchto vecí, počet zámkov sa zmení o párne číslo. A keďže na začiatku je odomknutých zámkov v skupine nula, teda tiež párny počet, tak odomknutých zámkov bude párny počet vždy. To znamená, že sa nám nikdy nemôže podariť odomknúť celý nepárny počet zámkov. Ukázali sme teda, že pri nepárnom počte zámkov vždy vieme odomknúť aspoň všetky až na jeden zámok, ale nikdy nie všetky.
Teraz už vieme ľahko vypočítať, koľko zámkov sa nedá otvoriť. Je ich práve toľko, koľko je nepárnych skupín zámkov, pretože v každej z nich jeden zámok nemôžeme otvoriť. A z ostatných skupín vieme otvoriť všetky zámky, lebo sú párne. Najmenšia nepárna skupina má veľkosť tri, pretože každá skupina musí mať veľkosť aspoň dva. Teda najviac nepárnych skupín, koľko môžeme vytvoriť, je 47 \div 3 = 15 (so zvyškom 2). To znamená, že najmenej 47-15 = 32 zámkov vieme otvoriť vždy a teda neexistuje rozostavenie, pri ktorom by sa dalo otvoriť zámkov iba 31. Zároveň máme príklad stavu, pri ktorom sa dá odomknúť iba 32 zámkov (existuje v ňom 47-32=15 nepárnych skupín): skladá sa z pätnástich skupín veľkosti tri a jednej skupiny veľkosti dva.
Komentár
Často sme strhávali body za nedostatočné zdôvodnenie toho, prečo sa v párnych skupinách dajú všetky zámky odomknúť, a prečo sa v nepárnych dajú odomknúť práve všetky až na jeden. Tieto kroky sme nepovažovali za samozrejmé.
9. príklad
Cieľom hrdinov je hrať tak, aby sústava mala na konci aj iné riešenie ako x = y = z = 0. Našou úlohou teda je nájsť víťaznú stratégiu pre hrdinov. Ak takú nájdeme, máme dokázané, že hrdinovia vedia hrať tak, aby splnili svoj cieľ. Tiež je nám jedno, aké bude toto nenulové riešenie, len nejaké musí byť. Zvoľme si teda jedno konkrétne riešenie a zistime ako musia hrdinovia ťahať, aby sa k nemu dostali.
Pre jednoduchosť zvolíme riešenie x = y = z = 1. Pozrime sa teda, čo musí platiť pre nejakú rovnicu s koeficientami a,\, b,\, c a riešením so samými jednotkami.
a + b + c = 0
Hrdinovia teda potrebujú, aby súčet doplnených čísel v každom riadku bol rovný 0. To vedia veľmi ľahko zariadiť, pokiaľ doplnia posledné číslo v danej rovnici. Ak sú už nejaké dve čísla a,\, b doplnené, doplnia c = -(a+b). Podobne však vie Jerguš zariadiť, aby súčet nebol 0. Stačí mu doplniť posledné číslo, iné ako to, ktoré by doplnili hrdinovia.
Pozrime sa teda, ako majú hrdinovia postupovať, aby v každej rovnici doplnili posledné číslo. V prvom kroku doplnia ľubovoľné prvé číslo do niektorej rovnice, bez újmy na všeobecnosti, nech je to prvá. Jerguš teraz môže doplniť buď do rovnakej ako hrdinovia, alebo do inej.
Ak doplnil do rovnakej, už sú v danej rovnici dve čísla. Hrdinovia do nej musia doplniť posledné, inak by im Jerguš mohol prekaziť plány. Tu si môžeme všimnúť, že ak by hrdinovia niekedy doplinili do rovnice druhé číslo, Jerguš im dokáže pokaziť ich plány. Ak je teda prvá rovnica celá vyplnená, Jerguš umistni číslo do niektorej z dvoch zvyšných a hrdinovia doplnia do poslednej. Potom Jerguš bude musieť doplniť druhé číslo do niektorej rovnice a hrdinovia doplnia posledné. To isté sa zopakuje aj pri poslednej rovnici.
Ak Jerguš doplnil vo svojom prvom ťahu do inej rovnice, vieme už, že hrdinovia musia doplniť do zvyšnej. Nesmú totiž v žiadnej doplniť druhé číslo. Potom sa dostáva Jerguš opäť do pozície, kde musí do niektorej rovnice doplniť druhé číslo. Hrdinovia potom doplnia v danej rovnici posledné číslo tak, aby súčet doplnených čísel vyšiel 0. Jerguš bude mať opäť rovnakú situáciu, keďže v rovniaciach, ktoré ešte nie sú doplnené, bude len jedno doplnené. Jerguš tak aj do zvyšných dvoch rovníc doplní druhé číslo a hrdinovia hneď za ním to posledné.
Riešenie 2:
Vieme, že pokiaľ by mala sústava rovníc iba dve rovnice o troch neznámych, vyšlo by nám buď nekonečne veľa riešení, alebo žiadne. Keďže v tomto prípade existuje riešenie x = y = z = 0, bude platiť druhá možnosť. Sústava teda bude mať aj iné riešenie a teda aj nenulové. Ako spraviť z troch rovníc iba dve? Najjednoduchšie spôsoby sú vynulovať jednu celú rovnicu alebo zariadiť, aby jedna rovnica bola násobkom druhej. My sa pokúsime nájsť spôsob, ako s hrdinami zariadiť druhý prípad z týchto.
Povedzme, že chceme, aby druhá rovnica bola k-násobkom prvej. Hrdinom je potom jedno, ako bude vyzerať tretia rovnica. V prvom kroku teda doplnia ľubovoľné číslo práve do tretej rovnice. Zvyšné miesta potom tvoria štyri dvojice: koeficienty pred x v prvých dvoch rovniciach, koeficienty pred y v prvých dvoch rovniciach, koeficienty pred z v prvých dvoch rovniciach a zvyšné dva koeficienty v tretej rovnici. Ak Jerguš doplní číslo na niektoré miesto, hrdinovia vedia vždy doplniť miesto, ktoré je s ním v dvojici. Ak je táto dvojica v tretej rovnici, môžu doplniť ľubovoľne. Ak dopĺňajú v druhom riadku, chcú doplniť číslo k-krát väčšie ako Jerguš doplnil v prvom. Naopak ak dopĺňajú v prvom riadku, chcú doplniť číslo k-krát menšie ako je v druhom riadku.
Vidíme, že koeficienty v druhej rovnici sú k-násobkami koeficientov prvej rovnice. Keďže navyše 0 \cdot k = 0, vidíme, že na voľbe k nezávisí, pokiaľ sa ním dá násobiť a deliť. Hrdinovia si tak môžu vybrať ľubovoľné reálne číslo okrem 0 a zaistia si výhru.
Komentár:
Úloha sa dala riešiť aj inými spôsobmi. Napríklad vedeli hrdinovia zariadiť, aby bola buď jedna rovnica nulová alebo jedna premenná mala pred sebou iba nuly. Výsledných sústav, ktoré mohli hrdinovia dosiahnuť bolo naozaj veľa, všetky riešenia však potrebovali zopár základných vecí:
- vysvetlenie, prečo takáto sústava má aj iné riešenie ako samé nuly;
- popis, ako sa k danej sústave dostanú. Tu trebalo popísať nielen kam, ale aj aké čísla hrdinovia dopĺňajú. Rovnako bolo nutné počítať s tým, že Jerguš hrdinom pomáhať nemusí.
Prémia 1
| číslo | výraz |
|---|---|
| 1 | \frac{4}{4} |
| 2 | \sqrt4 |
| 3 | 4-\frac{4}{4} |
| 4 | 4 |
| 5 | 4+\frac{4}{4} |
| 6 | \frac{4!}{4} |
| 7 | \frac{4+4!}{4} |
| 8 | 4+4 |
| 9 | 4+4+4/4 |
| 10 | 4+4+\sqrt4 |
| 11 | \frac{44}{4} |
| 12 | \frac{4!}{\sqrt4} |
| 13 | \frac{{\sqrt4+4!}}{\sqrt4} |
| 14 | \frac{4!}{\sqrt4}+\sqrt4 |
| 15 | 4^{\sqrt4}-4/4 |
| 16 | 4\cdot4 |
| 17 | 4\cdot4+4/4 |
| 18 | 4\cdot4+\sqrt4 |
| 19 | 4!-4-\frac{4}{4} |
| 20 | 4!-4 |
| 21 | 4!+\frac{4}{4}-4 |
| 22 | 4!-\sqrt4 |
| 23 | 4!-\frac{4}{4} |
| 24 | 4! |
| 25 | 4!+\frac{4}{4} |
| 26 | 4!+\sqrt4 |
| 27 | 4!+4-\frac{4}{4} |
| 28 | 4!+4 |
| 29 | 4!+4+\frac{4}{4} |
| 30 | 4!+4+\sqrt4 |
| 31 | 4!+\frac{4!+4}{4} |
| 32 | (4+4)\cdot4 |
| 33 | \sqrt4+\frac{\sqrt{\sqrt{\sqrt{4^{4!}}}}}{\sqrt4} |
| 34 | 4!+4+4+\sqrt4 |
| 35 | 4!+\frac{44}{4} |
| 36 | 4!/\sqrt4+4! |
| 37 | 4!+\frac{4!+\sqrt4}{\sqrt4} |
| 38 | 4!+4\cdot4-\sqrt4 |
| 39 | 4!+4\cdot4-4!+\frac{4}{4} |
| 40 | 4!+4\cdot4 |
| 41 | \sqrt{\frac{4!+(4+4)!}{4!}} |
| 42 | 44-\sqrt4 |
| 43 | 44-\frac{4}{4} |
| 44 | 44 |
| 45 | 44+\frac{4}{4} |
| 46 | 44+\sqrt4 |
| 47 | 4!+4!-\frac{4}{4} |
| 48 | 4!+4! |
| 49 | 4!+4!+\frac{4}{4} |
| 50 | 4!+4!+\sqrt4 |
Hodnotenie
153 až 155 použitých čísel - 7 bodov156 až 157 použitých čísel - 6 bodov
158 až 162 použitých čísel - 5 bodov
163 až 170 použitých čísel - 4 body
171 až 190 použitých čísel - 3 body
191 až 199 použitých čísel - 2 body
200 a viac použitých čísel - 1 bod