Vzorové riešenia 2. kola
1. príklad
Na začiatok si môžeme zjednodušiť príklad tým, že namiesto priemeru použijeme súčty. Tento krok nie je nutný k správnemu riešeniu, ale bude sa nám vďaka nemu ľahšie opisovať postup celého riešenia. Priemerné umiestnenie dvoch súťažiacich sa rovná polovici súčtu ich umiestnení, takže ak ich priemer vynásobíme dvomi, dostaneme súčet miest, na ktorých sa umiestnili. Tieto súčty sú pre súťažiacich z Aldebaranu(A) 11, z Boötes(B) 18, od Canopusu(C) 15, pre Delfínov(D) 6 a od Electry(E) 5.
Teraz sa pokúsime postupne pre rôzych súťažiacich nájsť dôvod, prečo iba jedna z možností, ako sa mohli umiestniť, bude správna. To sa nám oplatí spraviť naprv pre najextrémnejší súčet, ktorý majú B. Tu existuje iba jedna možnosť ako sa mohli umiestniť - na 8. a 10. mieste. Ak by sa ani jeden z nich neumiestnil na 10. mieste, Aj keby sa umiestnili najhoršie možne, na 8. a 9., súčet ich umiestnení by bol príliš nízky - 17.
Niektoré z vysokých umiestnení už máme obsadené, preto sa znova pozrieme na niekoho s vysokým súčtom, ďalší v poradí sú C so súčtom 15. Ich možnosti umiestnenia sú 10+5, 9+6, 8+7. Možnosť 10+5 však už má obsadené desiate miesto, a možnosť 8+7 ôsme. Inak sa dalo povedať, že ak by C nebol na 9. mieste, tak by mohol mať najviac súčet 7+6=13, čo je málo.
Podobným spôsobom pokračujeme - tentokrát pre súťažiacich A. Tí sa museli umiestniť na 7. mieste, lebo ak by sa na ňom neumiestnili, tak by ich súčet mohol byť najviac 5+4=9. Teda z možných umiestnení 10+1, 9+2, 8+3, 7+4, 6+5 to bude umiestnenie 7+4, a môžeme vidieť, že naozaj každé iné umiestnenie má už jednu pozíciu obsadenú.
Teraz nám ostávajú nám voľné už len miesta 1,2,3 a 5, pre D s priemerom 6 a E s priemerom 5. Priemer 6 vytvoríme jedine dvojicou umiestnení 1 a 5, lebo možnosť 2 a 4 nejde spraviť - 4. miesto obsadzuje jeden z A. Posledné dve miesta - 2 a 3 teda budú patriť E.
Príklad sa dal riešiť aj trochu iným spôsobom, ktorý zvolila aj časť riešiteľov. V tomto riešení by sme začali pri D a E. Tí majú možnosti umiestnenia 1+5 a 2+4 pre D, a 1+4 a 2+3 pre E. Tu si môžeme všimnúť, že ak by sme pre E zvolili možnosť 1+4, obsadili by sme tým jedno miesto z oboch možností pre D, a teda D by sa nevedelo umiestniť. Preto sa E musí umiestniť na 2. a 3. mieste, z čoho vyplýva že D sa umiestnilo na 1. a 5., a z toho sa vieme podobne ako v prvom riešení vypracovať k jediným možnostiam pre všetkých súťažiacich.
Odpoveď: Súťažiaci sa umiestnili nasledovne:
- Delfín
- Electránec
- Electránec
- Aldebrančan
- Delfín
- Canopusan
- Aldebračan
- Boötesčan
- Canopusan
- Boötesčan
2. príklad
Vzorové riešenie:
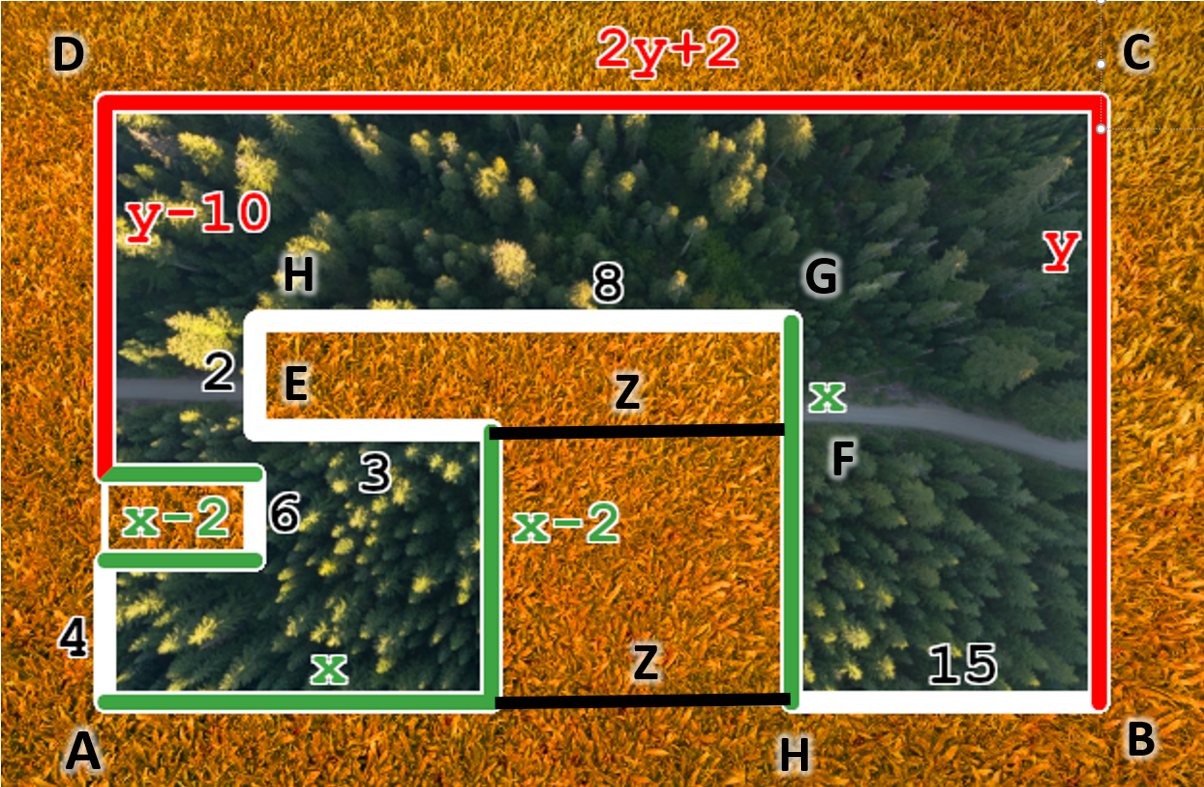
Keďže všetky uhly na obrázku sú pravé, tak útvar ABCD je obdĺžnik. Preto |AB|=|DC|. Veľkosti AB a DC, však vieme vyčítať z obrázku.
2 \cdot Y+2=|DC|=|AB|=X+Z+15
X+Z+15=2 \cdot Y+2
Teraz môžeme vyjadriť veľkosť Z. K tomu nám pomôže útvar EFGH, ktorý je obdĺžnikom. Preto vieme, že |EF|=|GH|. Ich veľkosť je znovu na obrázku:
Z+3=|EF|=|GH|=8
8=Z+3
5=Z
To môžeme dosadiť do skoršej rovnice:
X+Z+15=2 \cdot Y+2
X+5+15=2 \cdot Y+2
X=2 \cdot Y-18
Teraz na pravej strane máme rozdiel dvoch párnych čísel, ten je vždy párny. Keďže ľavá a pravá strana sa rovnajú, tak môžeme povedať, že aj ľavá strana, X, je párna.
Druhé kľúčové pozorovanie bolo, že Y-1 \geq X, na toto sa dalo prísť pri pohľade na stranu GH a CB, keby X \geq Y, tak strana HG by sa dotýkala, alebo by sa krížila zo stranou DC. My však vieme, že X je to isté ako 2 \cdot Y-18, a teda aj 2 \cdot Y-18, musí byť menšie alebo rovné ako Y-1:
X=2 \cdot Y-18
Y-1 \geq X
Y-1 \geq 2 \cdot Y-18
17 \geq Y
Teraz sa pozrime na ľavý dolný roh:
1. možnosť: Úsečka HE nemôže byť vedľa toho ľavého cípiku, lebo je od ľavej strany toho obdĺžnika vzdialená X – 3 a ten cípik je od ľavej strany vzdialený X – 2, ich vzájomná vzdialenosť je teda:
X-3-(X-2)=-1
Môžeme teda vidieť, že by sa prekryli.
2. možnosť: Úsečka HE nemôže byť ani pod tým cípikom, lebo buď by sa HG dotýkalo spodnej steny toho ľavého cípiku, pre X = 3, alebo by sa EF dotýkalo AB, pre X = 2.
3. možnosť Aby teda EH bolo nad tým cípikom, tak X>12, lebo:
X-2>6+4
X>12
Jediné párne hodnoty X, ktoré nám ostávajú sú X=14 a X=16 . K nim si dopočítame hodnoty Y, dostaneme Y=16 a Y=17. Oba prípady overíme obrázkom.
Pre dvojicu X=14 a Y=16 , to vizerá takto:
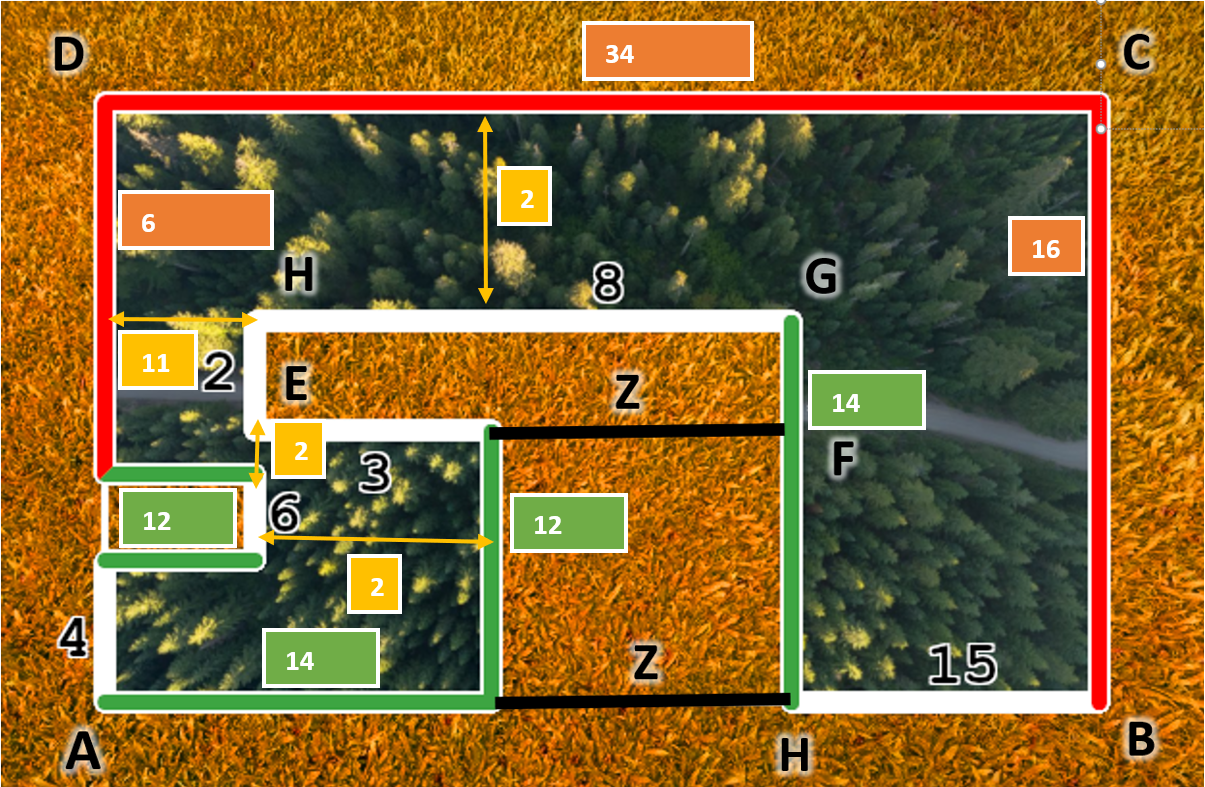
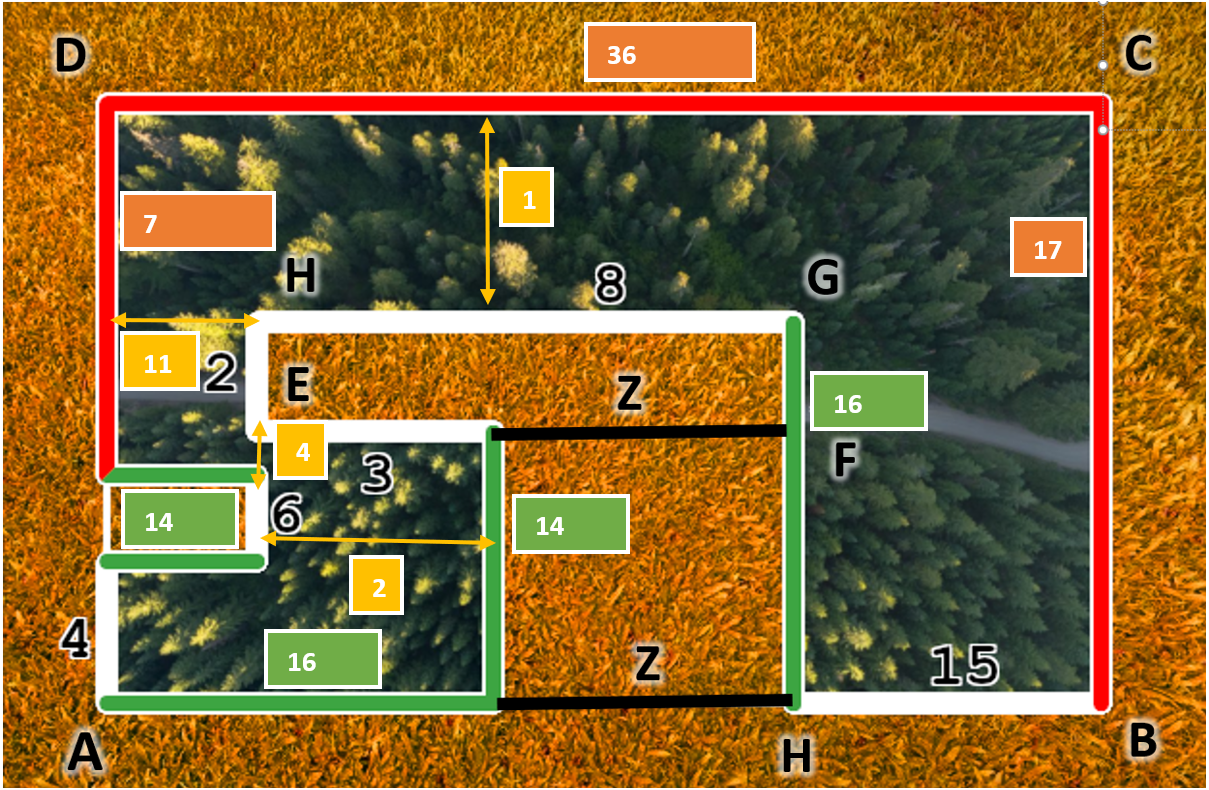
Pre dvojicu X=16 a Y=17 , to vizerá takto:
Celkovo väčšina z vás to veľmi pekne zvládla, občas tam boli dáke drobnosti.
3. príklad
Riešenie rovnicou
Označme si počet krabíc 3x, čiže v každej máme x krabíc svojho druhu. Sviňa začala jesť z ľava a nakoľko nevieme, aká je hodnota x, nevieme ani, či jedla iba z prvej tretiny, z prvej a druhej tretiny alebo zo všetkých troch tretín. Tu nastáva teda delenie na tri prípady.
Treba si uvedomiť, že ak jedla z druhej tretiny, prvú musela zjesť celú a podobne ak jedla z tretej tretiny, prvú a druhú musela zjesť celú.
- Ak jedla iba z prvej tretiny, obrátený prípad by bol, že jedla iba z tretej tretiny. Rozdiel týchto prípadov má byť 33 porcií. Vytvorme rovnicu:
25 \cdot 8=25 \cdot 5+33
25 \cdot 3=33
75=33 - čo nie je pravda a táto možnosť nie je riešením - Ak jedla iba z prvej a druhej tretiny, obrátený prípad by bol, že jedla iba z tretej a druhej tretiny. Rozdiel týchto prípadov má byť 33 porcií. Opäť vytvorme rovnicu:
x \cdot 8+(25-x) \cdot 7=x \cdot 5+(25-x) \cdot 7+33
x \cdot 8=x \cdot 5+33
x \cdot 3=33
x=11 - ak by bolo ale 11 krabíc v každej tretine, znamenalo by to, že by svini stačilo zjesť 22 krabíc a dostala by sa k tretej tretine. Nakoľko zjedla 25 krabíc, jedla by zo všetkých troch tretín, čo nie je zahrnuté v tejto možnosti. Teda to nie je riešením úlohy. - Ak jedla zo všetkých tretín, obrátený prípad by bol, že jedla stále zo všetkých tretín. Rozdiel týchto prípadov má byť 33 porcií. Vytvorme rovnicu:
x\cdot8+x\cdot7+(25-2\cdot x)\cdot5=x\cdot5+x\cdot7+(25-2\cdot x)\cdot8+33
x\cdot8+(25-2\cdot x)\cdot 5=x\cdot5+(25-2\cdot x)\cdot 8+33
x\cdot8+125-10\cdot x=x\cdot 5+200-16\cdot x+33
125-2\cdot x=233-11\cdot x
9\cdot x=108
x=12 - po 24 krabiciach by sa sviňa dostala k tretej tretine a jednu krabicu by zjedla z tretej tretiny, čo táto možnosť zahŕňa. 12 krabíc v jednej tretine a teda 36 krabíc na chodbe je správne riešenie.
Riešenie skúšaním
Pri skúšaní musíme jednoducho vyskúšať všetky možnosti počtu krabíc. Môžeme (a aj musíme) si to ohranič zdola aj zhora.
Ak by bolo v každej tretine 8 a menej krabíc, spolu by ich nebolo ani 25 a sviňa by vtedy len veľmi ťažko zjedla obsah prvých 25 krabíc z ľava.
Ak by bolo v každej tretine 25 a viac krabíc, rozdiel by sme už nevideli, lebo sviňa by tak-či-tak zjedla krabice len z prvej tretiny.
Bodovanie
- -2b ak ste nenapísali všetky rovnice, no iba tú, z ktorej výjde riešenie (ak ste nevysvetlili, prečo iné riešania byť nemôžu)
- -1b ak ste pri skúšaní nevysvetlili, prečo začínate tam, kde začínate
- -2b ak ste pri skúšaní nevysvetlili, prečo končíte tam, kde končíte
- -2b ak ste pri skúšaní iným spôsobom nevysvetlili všetky možnosti
- 1b ak ste napísali iba výsledok
- za rôzne individuálne chyby (spomenuté vo vašom riešení) ste mohli stretiť ďalšie body
4. príklad
Teda to, ako Maťko počíta vyzerá nejak takto:
| číslo | 1 | 2 | 3 |
4 | 5 | 6 | 7 | 8 |
| písmeno prstu | A | B | C |
D | E | D | C | B |
| číslo | 1 | 2 | 3 |
4 | 5 | 6 | 7 | 8 |
| písmeno prstu | A | B | C |
D | E | D | C | B |
| číslo | 1 | 2 | 3 |
4 | 5 | 6 | 7 | 8 |
| písmeno prstu | A | B |
C |
D |
E | D | C | B |
Všimnime si, že po ôsmich prstoch sme naspäť na palci a potom sa to opakuje. To by nás pravdaže nemalo nijak prekvapiť, keďže stále ukazujeme na prsty úplne rovnako.
To znamená, že sa tento "blok" ôsmich prstov sa nám bude hodne veľa krát opakovať. Nás by zaujímalo pokiaľ, takže by sa hodilo nájsť také číslo, ktoré je menšie ako 2020 a zároveň je deliteľné číslom 8. Taktiež by sme takéto číslo chceli čo najväčšie, lebo číslo 24 síce spĺňa požiadavky, no veľmi nám nepomôže. Preto chceme také *najväčšie* číslo.
Po chvíli hľadania prichádzame na to, že toto číslo je 2016. Pamätajme, že na tomto čísle ukazujeme na prst B, teda ukazovák. Treba ešte tie zvyšné 2020 - 2016 = 4 prsty dopočítať, teda: palec, ukazovák, prostredník, prstenník.
Výsledok je teda prstenník.
5. príklad
Číslo yxxy si vieme zapísať aj ako 1000y+100x+10x+y=1001y+110x. Vieme o ňom, že má byť deliteľné 7. 1001y vo svojom prvočíselnom rozklade 7 obsahuje (lebo 1001=143·7), takže na to, aby aj výsledné yxxy bolo deliteľné 7 musí byť aj 110x deliteľné 7. Keďže 110 nie je deliteľná 7, tak x musí byť deliteľné 7, no a jediné také nenulové x=7.
Pozrime sa teraz na číslo xxzx (podľa prvého odstavca 77z7). Ak je toto číslo deliteľné 3, potom musí byť jeho ciferný súčet deliteľný 3, teda x+x+z+x musí byť delitelné 3. Keď si to prepíšeme, tak 21+z musí byť deliteľné 3. 21 deliteľná 3 už je, teda z musí byť tiež deliteľné 3. Z je potom buď 3, 6 alebo 9.
Keď sa pozrieme na číslo xyz, tak ak je deliteľné 46, tak musí byť aj všetkými jeho deliteľmi (1, 2, 23, 46). Ak je číslo deliteľné 2, potom jeho posledná cifra je párna. Keď to spojíme s podmienkou z predchádzajúceho riadku, tak vieme, že z=6.
Vieme, že číslo xyz sa dá zapísať ako 7y6. Teraz už len vypíšeme všetky čísla, ktoré sú menšie ako 800 a väčšie ako 700 a pozrieme sa, ktoré z nich vyhovujú našim podmienkam:
736 - vyhovuje
782 - posledná cifra nie je 6
Väčšie ani menšie čísla delitelné 46 v intervale od 700 do 800 nie sú a preto je x=7, y=3, z=6 jediným riešením.
6. príklad
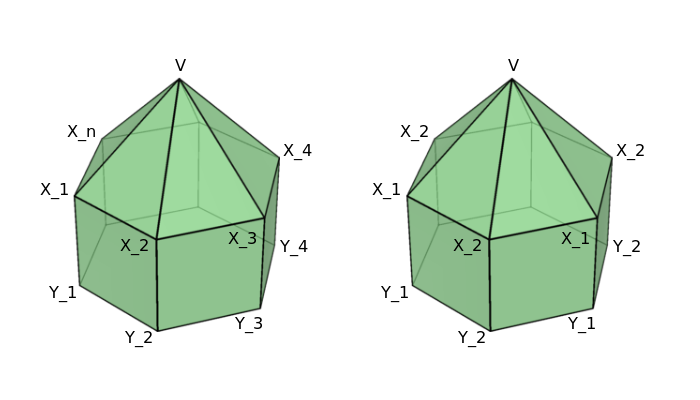
V prvom rade si označíme niektoré veci. Počet vrcholov (= počet strán) podstavy ihlanu budeme značiť n. Hodnotu v hornom vrchole ihlanu označíme v. Hodnoty vrcholov v podstave ihlanu nazveme postupne x_1, x_2, \dots, x_n. Na záver vrcholy v dolnej podstave hranola označíme y_1, y_2, \dots, y_n. (viď ľavý obrázok)
Teraz sa pozrime na ľubovoľné dve susedné steny ihlanu. Majú spoločný jeden horný vrchol s hodnotou v a jeden dolný vrchol s hodnotou x_{i}. Keďže majú ale steny rovnaký súčet musia mať aj zostávajúce nespoločné vrcholy rovnakú hodnotu. (Napr. ak x_{i} = x_2, tak to znamená, že x_1 je to isté ako x_3). Z toho vyplýva, že hodnoty vo vrcholoch podstavy ihlanu sa na preskačku striedajú. Inými slovami, x_1 = x_3 = x_5 = \dots a x_2 = x_4 = x_6 = \dots. Dokonca si môžeme všimnúť, že ak n (počet vrcholov podstavy ihlanu) je nepárny, tak predchádzajúce odvodenie hovorí, že musia byť všetky hodnoty vo vrcholoch podstavy rovnaké, teda x_1 = x_2 = x_3 = \dots.
Podobnú úvahu môžeme urobiť aj pre bočné steny hranola. Každá bočná stena hranola obsahuje 4 vrcholy - dva z hornej podstavy a dva z dolnej. Navyše, tie dva z hornej majú v nejakom poradí hodnoty x_1, x_2 a teda majú súčet x_1+x_2. Pozrime sa teraz na dve susedné bočné steny. Majú spoločný jeden vrchol v dolnej podstave y_i. Zároveň každá má dva vrcholy v hornej podstave, ktoré v súčte dávajú x_1+x_2. A obe steny majú rovnaký súčet. To ale znamená, že ich nespoločné vrcholy v dolnej podstave musia mať rovnakú hodnotu. Aj v dolnej podstave to teda bude vyzerať na preskačku: y_1 = y_3 = y_5 = \dots a y_2 = y_4 = y_6 = \dots. A v prípade, že je n nepárne, sú všetky hodnoty v dolnej podstave rovnaké.
Čo sa to deje ak n je nepárne? Dostávame v celom obrázku najviac 3 rôzne hodnoty v (úplne navrchu), x_1 (v podstave ihlanu) a y_1 (v dolnej podstave hranola). Lenže podľa zadania tam majú byť aspoň 4 hodnoty: 7, 8, 9, 216. n nepárne teda nevychádza a ďalej teda predpokladáme, že n je párne.
Situáciu máme znázornenú na pravom obrázku. Ostalo nám 5 rôznych nezámych v, x_1, x_2, y_1, y_2. Máme im priradiť 5 hodnôt 7, 8, 9, 216, H. Aby sme zistili, čo priradiť čomu, poďme vyjadriť súčty na jednotlivých stenách útvaru:
- trojuholníková stena na ihlane má vždy súčet v+x_1+x_2,
- štvorcová bočná stena hranola má vždy súčet x_1+x_2+y_1+y_2,
- spodná stena podstavy hranola má súčet (y_1+y_2) \cdot\dfrac{n}{2}.
Všetky tieto výrazy majú podľa zadania rovnakú hodnotu.
Z rovnosti prvých dvoch výrazov vyplýva v = y_1+y_2. Z tohto vzťahu vidíme, že jedno z čísel v, y_1, y_2 je H, lebo medzi číslami zo zadania nie sú tri také, že jedno je súčet zvyšných dvoch. Potom ale čísla x_1, x_2 sú obe niektoré zo štyroch zadaných čísel.
Pozrime sa na rovnosť druhého a tretieho výrazu. Dostávame x_1+x_2+y_1+y_2 = (y_1+y_2) \cdot\dfrac{n}{2} a upravíme do tvaru x_1+x_2 = (y_1+y_2)(\dfrac{n}{2}-1). Keďže počet vrcholov podstavy n je aspoň 4, pravá strana rovnice je aspoň (y_1+y_2). Takže aj ľavá strana rovnice musí byť, inými slovami x_1+x_2 \geq y_1+y_2.
Ďalej si všimneme, že x_1 alebo x_2 je 216. Ak by to tak nebolo, tak x_1+x_2 by bolo najviac 8+9 = 17. Avšak y_1, y_2 alebo v = y_1+y_2 by muselo byť 216 a teda by platilo y_1+y_2 \geq 216. Tým by ale bola porušená nerovnosť odvodená v predošlom odseku. Keďže x_1, x_2 sú z pohľadu riešenia zameniteľné, môžeme si povedať, že x_1 = 216.
Ostáva doriešiť 3 možnosti pre x_2:
- x_2 = 7: Vidíme, že v \geq y_1, y_2. Tu preto vznikajú dve možnosti y_1 = 8, y_2 = 9, v = H a y_1 = 8, y_2 = H, v = 9. V prvej vychádza v = y_1+y_2 = 17. Avšak vieme, že (y_1+y_2)\cdot\dfrac{n}{2} = (x_1+x_2+y_1+y_2), teda (ak vyjadríme n) máme n = \dfrac{2(x_1+x_2+y_1+y_2)}{y_1+y_2}. Dosadíme: n = \dfrac{2\cdot(7+216+8+9)}{8+9}, čo ale nie je celé číslo. V druhej možnosti H = 9-8 = 1. Potom použijeme rovnaký vzťah pre výpočet n a dostaneme n = \dfrac{2\cdot(7+216+8+1)}{8+1}, čo ale opäť nie je celé číslo. Takže v tejto vetve nemáme žiadne riešenia.
- x_2 = 8: Opäť využijeme v \geq y_1, y_2 a tak stačí preveriť y_1 = 7, y_2 = 9, v = H a y_1 = 7, y_2 = H, v = 9. V oboch prípadoch odvodíme hodnotu H a použijeme vzorec pre n. Prvá možnosť dáva riešenie n = 30. Skutočne n = 30, x_1 = 216, x_2 = 8, y_1 = 7, y_2 = 9, v = 16 je riešenie. Druhá možnosť (podobne ako v predošlom bode) nevýjde.
- x_2 = 9: Opäť preveríme y_1 = 7, y_2 = 8, v = H a y_1 = 7, y_2 = H, v = 8. Znova vykonáme ten istý postup. Prvá možnosť vedie k riešeniu n = 32. Skutočne n = 32, x_1 = 216, x_2 = 9, y_1 = 7, y_2 = 8, v = 15 je riešenie. Druhá možnosť nevýjde.
Riešením sú teda 30 a 32.
7. príklad
 Riešenie:
Riešenie:
Body D, S ležia v stredoch strán BC, AC, teda úsečky AD, BS sú ťažnice v trojuholníku ABC. Priesečník ťažníc je ťažisko, teda bod E je ťažisko trojuholníka ABC.
Ťažisko delí ťažnicu v pomere 2:1, teda dĺžka |AE| je dva krát dlhšia ako dĺžka |ED|. Bod F je v strede úsečky AE, teda |AF| = |FE|. Keďže vieme, že úsečka ED je dva krát kratšia ako úsečka AE, tak musí platiť že |AF| = |FE| = |ED|.
Teraz sa pozrime na trojuholník ABD. V tomto trojuholníku máme dve rovnako dlhé strany, a to AB, BD, lebo 2|AB| = |BC|, a zároveň D leží v strede BC, teda 2|BD| = |BC|. Keď dáme tieto rovnosti dokopy, tak dostaneme 2|AB| = |BC| = 2|BD|, teda |AB| = |BD|.
Trojuholník, ktorý má dve strany rovnako dlhé nazývame rovnoramenný a platí v ňom, že uhly pri základni má rovnako veľké. Základňa je v tomto prípade strana AD, teda platí |\measuredangle BAD| = |\measuredangle ADB|.
Dostali sme teda tri zaujímavé rovnosti. Konkrétne |AF| = |ED|, |AB| = |BD|, |\measuredangle BAD| = |\measuredangle ADB|. Podľa vety SUS sú potom trojuholníky AFB a DEB zhodné, čím musia byť zhodne veľké aj uhly ABF, EBD.
8. príklad
Majme nejakých 39 po sebe idúcich čísel. Z pomedzi nich si nájdeme prvé ktoré končí nulou a označíme ho x. Bude to najneskôr desiate číslo, čo znamená, že od tohto čísla až po posledné číslo máme aspoň 30 čísel.
Teraz nás budú zaujímať len čísla x až x+29. Môžme si všimnúť, že týchto 30 čísel vieme rozdeliť na 3 desatice v rámci ktorých sa mení len posledná cifra. To znamená, že ciferné súčty v každej tejto desatici tvoria 10 po sebe idúcich čísel. No a aby žiadne z týchto čísel nebolo deliteľné 11, musí mať prvé z nich zvyšok 1, druhé zvyšok 2 atď.
Takže už vieme, že jediná možnosť kedy nie je ani jedno z čisel deliteľné 11, je keď ciferné súčty x, x+10 aj x+20 majú zvyšok 1 po delení 11.
Môže toto nastať? Pozrime sa ako sa menia cifry medzi x, x+10 a x+20. Rozdelíme si to na 2 prípady:
- Ak číslo x nemá na mieste desiatok 9, čísla x a x+10 sa budú líšiť len v tejto cifre a ich ciferné súčty sa budú líšiť o 1. To znamená, že nemôžu mať oba zvyšok 1.
- Ak číslo x má na mieste desiatok 9, číslo x+10 tam bude mať 0 a teda to isté bude platiť o číslach x+10 a x+20.
To znamená, že niektoré z nich nebude mať zvyšok 1 a teda nejaké z našich 39 čísel bude mať ciferný súčet deliteľný 11.
Poznámka: ak by sme brali len 38 po sebe idúcich, čísel tvrdenie by neplatilo. Protipríklad sú čísla 999981 až 1000018.
9. príklad
Pozrime sa na to, ako bude vyzerať šachovnica na konci hry. Ak by na konci hry boli v nejakom riadku alebo stĺpci iba bezpečné políčka, tak by si ešte daný riadok alebo stĺpec mohla vybrať strana, ktorá je na ťahu. Tým pádom by to nemohol byť koniec hry. Na konci hry teda musí byť v každom riadku a v každom stĺpci na šachovnici aspoň jedno nebezpečné políčko.
Z toho teda vyplýva, že na konci hry existujú aspoň dve nebezpečné políčka, ktoré sú v navzájom rôznom riadku aj stĺpci. Pozrime sa teraz na tieto dve nebezpečné políčka, ktoré si na obrázku označíme čiernou farbou. Ak sa prvé z týchto políčok nachádza v k-tom riadku a x-tom stĺpci, tak sa mohlo zmenšiť len vybratím k-tého riadku alebo x-tého stĺpca. Keďže sa dané políčko zmenšilo o 99, tak súčet počtu vybratí k-tého riadku a počtu vybratí x-tého stĺpca za celú hru musel byť 99. Pozrieme sa teraz na druhé nebezpečné políčko, ktoré je v l-tom riadku a v y-tom stĺpci. Takisto musí platiť, že súčet počtu vybratí l-tého riadku a y-tého stĺpca za celú hru musel byť 99.
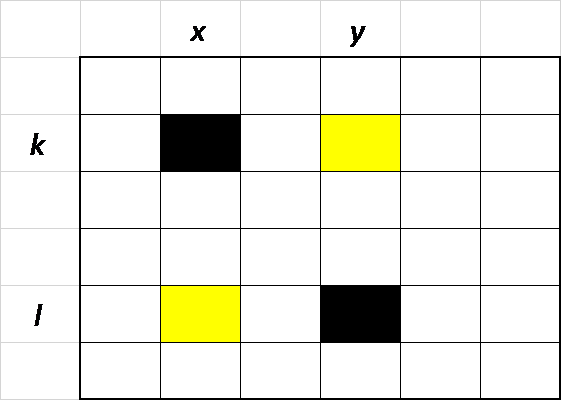
Označme si k_v ako počet vybratí k-tého riadku, l_v ako počet vybratí l-tého riadku, x_v ako počet vybratí x-tého stĺpca a y_v ako počet vybratí y-tého stĺpca. Naše poznatky si vieme zapísať do nasledujúcich dvoch rovníc
Sčítaním rovníc dostaneme
Pozrime sa teraz na žlté políčko v k-tom riadku a y-tom stĺpci. Jeho hodnota sa od začiatku hry zmenšila o súčet počtov vybratí k-tého riadku a y-tého stĺpca. Preto na ňom musí byť na konci hry hodnota
Takisto keď sa pozrieme na žlté políčko v l-tom riadku a v x-tom stĺpci, jeho hodnota musí byť
Z využitím zistených poznatkov vieme, že súčet hodnôt na týchto dvoch žltých políčkach na konci hry je
Keďže žiadne z políčok nemôže nadobúdať zápornú hodnotu, tak obidve políčka musia mať hodnotu 0 na konci hry a byť nebezpečné.
Pozrime sa teraz na hodnotu ľubovoľného políčka na šachovnici na konci hry. Vieme, že na konci hry musí byť v každom riadku a v každom stĺpci aspoň jedno nebezpečné políčko. Keďže v žiadnom riadku ani stĺpci nie sú iba bezpečné políčka, toto ľubovoľné políčko je buď nebezpečné, alebo sa nachádza v riadku s aspoň jedným nebezpečným políčkom a aj v tom istom stĺpci sa nachádza aspoň jedno nebezpečné políčko. Už sme dokázali, že ak sa zároveň nachádza v rovnakom riadku s nebezpečným políčkom aj v rovnakom stĺpci s nebezpečným políčkom, musí byť tiež nebezpečné. Z toho vyplýva. že naše políčko musí byť tiež nebezpečné na konci hry.
Dokázali sme, že ľubovoľné políčko na šachovnici musí byť na konci hry nebezpečné. Tým pádom musia byť na konci hry všetky políčka nebezpečné, teda mať hodnotu 0. Celkovo je na šachovnici n^2 políčok a všetkým sa za celú hru znížila hodnota o 99. Súčet hodnôt políčok na šachovnici sa teda znížil za celú hru o 99n^2. Každým ťahom sa zníži n políčkam hodnota o 1 a teda súčet hodnôt políčok na šachovnici sa zmení o n každým ťahom. Celkový počet ťahov, ktorý sa musel zahrať je
Pretože prehráva strana, ktorá už nemôže zahrať ťah, začínajúca strana vyhrá ak zahrá posledný ťah. To nastáva pokiaľ je počet ťahov za hru nepárny, čo pri počte ťahov 99n nastáva pri nepárnom n. Pri párnom n teda začínajúca strana prehrá, keďže vtedy je celkový počet ťahov párny.
Odpoveď: Začínajúca strana vyhrá pri nepárnom n.
Prémia 1
 Body sme udeľovali nasledovne:
Body sme udeľovali nasledovne:
- 15 - 8 bodov
- 14 - 5 bodov
- 13 - 4 body
- 11 až 12 - 3 body
- 10 - 2 body
- 9 a menej - 1 bod