Vzorové riešenia 1. kola
1. príklad
2. príklad
1. deň:
Pozrieme sa na to, čo povedal druhý radca: "Presne tak, ja aj 3.radca klameme." Ak by hovoril pravdu, tak by o sebe tvrdil, že klame. Ale potom by musel hovoriť aj pravdu aj klamstvo naraz, čo sa nedá a teda musí druhý radca klamať.
Keďže klame, tak to, že druhý aj tretí radca klamú je klamstvo, čiže pravdou je, že aspoň jeden z nich musí hovoriť pravdu. A teda, keďže druhý radca klame, tak tretí radca musí hovoriť pravdu. Potom je ale tvrdenie prvého radcu "Ostatní dvaja radcovia klamú." lož, lebo tretí hovorí pravdu.
Čiže sme zistili, že prvý radca klame, druhý radca klame a tretí hovorí pravdu. Keďže máme dvoch klamárov a iba jedného pravdovravného, tak musí platiť, že Zajo je hladný a klame, lebo Romanus klame vždy a Tetetínia vždy hovorí pravdu.
Tretí radca je teda Tetetínia, lebo ona musí hovoriť pravdu. Jej tvrdenie je: "Nie som hladný. Ani 2.radca nie je hladný." A teda druhý radca je sýty klamár a teda jedine Romanus. Potom je prvým radcom Zajo a keďže klame, tak je hladný.
Riešenie prvého dňa:
1.radca je hladný Zajo.
2.radca je sýty Romanus.
3.radca je sýta Tetetínia.
2. deň:
Pozrieme sa na tvrdenie tretieho radcu: "Obaja zvyšní radcovia majú pravdu. Ja som Zajo. Nie som hladný." Ak by hovoril pravdu, tak potom by museli hovoriť pravdu aj obaja zvyšní radcovia a teda by žiadny radca neklamal. Ale my vieme, že Romanus musí vždy klamať a teda tretí radca nemôže hovoriť pravdu a teda klame.
Potom pravdivé tvrdenia sú, že aspoň jeden radca spomedzi prvého a druhého radcu klame, tretí radca nie je Zajo a je hladný. Keďže tretí radca klame a zároveň nie je Zajo, tak to môže byť jedine Romanus.
Teraz si rozoberieme tvrdenia prvých dvoch radcov. Prvý radca hovorí: "Zajo nie je hladný." Ak by hovoril pravdu, tak by to znamenalo, že Aj Tetetínia aj Zajo budú hovoriť pravdu a teda by aj prvý aj druhý radca hovorili pravdu, čo ale nie je možné, lebo z výrokov tretieho radcu vieme, že aspoň jeden z nich klame. Čiže musí platiť, že prvý radca klame a teda to spomedzi Zaja a Tetetínie môže byť jedine Zajo, ktorý bude potom musieť byť hladný. Tetetínia potom bude musieť byť druhý radca.
Prvý radca Zajo teda klame a jeho tvrdenie, že Zajo nie je hladný je tým pádom klamstvo, čo sedí, lebo Zajo je hladný. Druhý radca Tetetínia hovorí pravdu a jej tvrdenia znejú: "Prvý radca klame. Ja som hladný." Jej prvé tvrdenie aj naozaj platí a aby platilo aj druhé, tak musí byť Tetetínia hladná. Tretí radca Romanus klame a jeho tvrdenia sú aj naozaj klamstvami, lebo prvý radca klame, on nie je Zajo ale Romanus a keďže tvrdí, že nie je hladný, tak v skutočnosti je hladný.
Riešenie druhého dňa:
1.radca je hladný Zajo.
2.radca je hladná Tetetínia.
3.radca je hladný Romanus.
3. deň:
V tento deň rozprával iba jeden radca a jeho tvrdenie bolo: "Volám sa Romanus." Ak by bol prvý radca Romanus, tak by jeho tvrdenie, že sa volá Romanus, bolo pravdivé, čo ale nemôže, lebo on vždy klame. Ak by bola prvým radcom Tetetínia, tak by jej tvrdenie, že sa volá Romanus, bolo klamstvo, čo ale nemôže, lebo ona vždy hovorí pravdu. Teda toto tvrdenie musel povedať Zajo a kvôli tomu, že sa nevolá Romanus, tak musel klamať, čiže bol hladný. Zároveň, keďže zvyšní dvaja radcovia neprehovorili, tak museli byť určite sýti.
Riešenie tretieho dňa:
1.radca je hladný Zajo.
Tetetínia a Romanus sú obidvaja sýti.
3. príklad
Pozrime sa na to, ako koňa Pejko II obmedzuje prvá podmienka (t.j. číslo každého z koní, okrem prvých dvoch, vynásobené samým sebou je väčšie ako súčet čísel dvoch predchádzajúcich koní). Ak sa Pejko II nachádza na prvej alebo druhej pozícii, všetko je v poriadku, lebo táto podmienka sa na tie dve pozície nevzťahuje. Ak sa Pejko II nachádza kdekoľvek inde, tak musí platiť, že súčet čísel dvoch predchádzajúcich koní je OSTRO menší ako 2 \cdot 2 = 4. Najmenšie dve čísla, ktoré môžu byť pred Pejkom II, sú čísla 1, 3. Lenže, už aj tieto najmenšie dve nám porušujú zadané pravidlo.
A samozrejme, dať tesne pred Pejka II väčšie čísla nám nijako nezlepší situáciu. Preto, podľa prvej podmienky, Pejko II smie byť iba na pozíciách číslo jeden alebo dva. Ak by sme teraz našli poradia, v ktorých sa Pejko II vyskytuje na práve týchto pozíciách (a obe zadané podmienky sú dodržané), tak sme vyhrali.
Uvážme najprv poradie 1,2,3,4,5,6,7,8. Prvá podmienka:- 1 + 2 = 3 \lt 9 = 3 \cdot 3
- 2 + 3 = 5 \lt 16 = 4 \cdot 4
- 3 + 4 = 7 \lt 25 = 5 \cdot 5
- 4 + 5 = 9 \lt 36 = 6 \cdot 6
- 5 + 6 = 11 \lt 49 = 7 \cdot 7
- 6 + 7 = 13 \lt 64 = 8 \cdot 8
- 1 \lt 5 = 2 + 3
- 2 \lt 7 = 3 + 4
- 3 \lt 9 = 4 + 5
- 4 \lt 11 = 5 + 6
- 5 \lt 13 = 6 + 7
- 6 \lt 15 = 7 + 8
Vidíme, že všetko sedí. Takže Pejko II môže byť na druhej pozícii.
Teraz uvážme (a overme) poradie 2,1,3,4,5,6,7,8.
- 2 + 1 = 3 \lt 9 = 3 \cdot 3
- 1 + 3 = 4 \lt 16 = 4 \cdot 4
- 3 + 4 = 7 \lt 25 = 5 \cdot 5
- 4 + 5 = 9 \lt 36 = 6 \cdot 6
- 5 + 6 = 11 \lt 49 = 7 \cdot 7
- 6 + 7 = 13 \lt 64 = 8 \cdot 8
- 2 \lt 4 = 1 + 3
- 1 \lt 7 = 3 + 4
- 3 \lt 9 = 4 + 5
- 4 \lt 11 = 5 + 6
- 5 \lt 13 = 6 + 7
- 6 \lt 15 = 7 + 8
Vidíme, že aj toto poradie vyhovuje. Tým sme ukázali, že na jediných povelených pozíciách (t.j. prvej a druhej pozícii) sa Pejko II môže nachádzať.
Odpoveď: Pejko II sa mohol nachádzať v poradí na prvom alebo druhom mieste.
4. príklad
Po chvíli skúšania rôznych taktík a stratégii nám napadne jednoduchý postup pre Lámača - vždy zoberie opak toho, čo vzal Paulus (Ak vzal Paulus 4, Lámač vezme 2. Ak vzal Paulus 2, Lámač vezme 4.).
Prečo je táto stratégia víťazná? Keďže Lámač vždy vezme opak toho, čo vzal Paulus, po každej dvojici ťahov (jeden Paulusov ťah a jeden Lámačov ťah) sa počet knedlí zníži presne o 2+4=6. To znamená, že po 7 dvojiciach ťahov bude na tanieri 42-7\cdot6 = 0 a na ťahu bude Paulus. Paulus nebude mať, čo urobiť a teda prehrá.
Víťazstvo si teda vie bez ohľadu na Paulusove ťahy zaručiť Lámač.
5. príklad
V geometrii je fajn si nakresliť obrázok, takže začnime s ním. Aby sa nám lepšie pracovalo, pomenujme si vrcholy, napríklad nasledovne:

Ako prvé by sme si mohli pripomenúť, že obrázky v zadaní nie sú presné a malo by sa v nich používať iba to, čo máte zadané a to, čo dokážete. Viacerí z vás používali fakt, že body A, D, C ležia na jednej priamke a potom ste dostávali nesprávne výsledky, pretože tento fakt je nepravdivý.
Máme teraz dve možné informácie, ktoré môžeme použiť, a tu sú dĺžky a pravé uhly. V tejto chvíli nám len dĺžky veľmi nepomôžu, takže treba nejako šikovne použiť pravé uhly. Pravý uhol BAE si necháme na neskôr, teraz sa sústreďme na dva zvyšné pravé uhly.
Zamerajme sa na úsečku CD. Vidíme, že úsečky BC a DE sú na ňu obe kolé, preto sú navzájom sú rovnobežné. Toto je veľmi dôležitý krok, ktorý veľa z vás zanedbalo. Predĺžme teraz úsečku BC na priamku, je zjavné, že aj celá táto priamka je kolmá na CD. Prenesme si teraz úsečku DE na túto priamku tak, aby bol bod D v bode C a takto bod E padne do nového bodu F. Samozrejme, že platí \left| DE\right| = \left| CF\right|. Vďaka pravouhlosti a rovnakých dĺžok platí, že \left| FE\right| = 4 a tiež, že úsečka FE je kolmá na priamku BC. Spojme ešte body B, E úsečkou a pozrime sa na nový obrázok:

Pozrime sa teraz na trojuholník FEB. Ten vieme, že je prevouhlý, jedna strana má dĺžku 4, druhá 8 a jeho najdlhšia strana, prepona, je červená úsečka. Ďalej, aj trojuholník AEB je pravouhlý, vidíme, že jeho prepona je červená úsečka a jedna z jeho strán má dĺžku 4. Teraz sa dalo pokračovať dvomi schodnými cestami, uvedieme obe.
Prvá možnosť využije to, že trojuholníky FEB, AEB sú zhodné podľa vety ssu o podobnosti trojuholníkov - červená úsečka, úsečka dĺžky 4 a pravý uhol. Zo zhodnosti vyplýva, že \left| FB\right| = \left| AB\right| a z toho vieme, že \left| AB\right| = 8, čo sme potrebovali zistiť.
Druhá možnosť používa Pytagorovu vetu pre pravouhlé trojuholníky. Z tejto vety vyplýva, v našom prípade, že \left| EB\right| = \sqrt{\left| EF\right|^2 + \left| FB\right|^2}, presnejšie teda \left| EB\right| = \sqrt{4^2 + 8^2} = \sqrt{80}. Teraz použime Pytagorovu vetu znovu, ale na trojuholník AEB a to v tomto znení: \left| AB\right| = \sqrt{\left| EB\right|^2 - \left| AE\right|^2}. Dosadíme: \left| AB\right| = \sqrt{\sqrt{80}^2 - 4^2} = \sqrt{64} = 8.
Obe metódy nám dali rovnaké riešenie (a to že \left| AB\right| = 8) čo je upokojujúce.
6. príklad
Zo zadania máme tri rovnice:
\begin{gathered}A+B+C=10\\B+C+D=10\\C+D+E=10\end{gathered}
Teda platí A+B+C=B+C+D, teda A=D. Taktiež platí B+C+D=C+D+E, teda B=E. Naše číslo má teda tvar \overline{ABCAB}.
Toto číslo sa dá rozpísať na: 10000A+1000B+100C+10A+B=10010A+1001B+100C. Zo zadania ale vieme, že toto číslo musí byť deliteľné 7. Keďže 10010A aj 1001B deliteľné 7 určite sú \lparen 10010\div7=1430,1001\div7=143\rparen, tak aj 100C musí byť deliteľné 7.
Keďže 100 nie je deliteľné 7, musí byť C deliteľné 7.
Teda C môže byť len 0 alebo 7.
Poďme teda vypísať možnosti:
- C=0 Potom A+B=10-0=10. Teda možnosti sú:
- C=7 Vieme, že A+B=10-7=3. Taktiež A môže byť len 1 až 9 (ak by platilo A=0, číslo by bolo štvorciferné). Teda možnosti sú:
19019,28028,37037,46046,55055,64064,73073,82082 a 91091
12712,21721 a 30730
7. príklad
Riešenie:
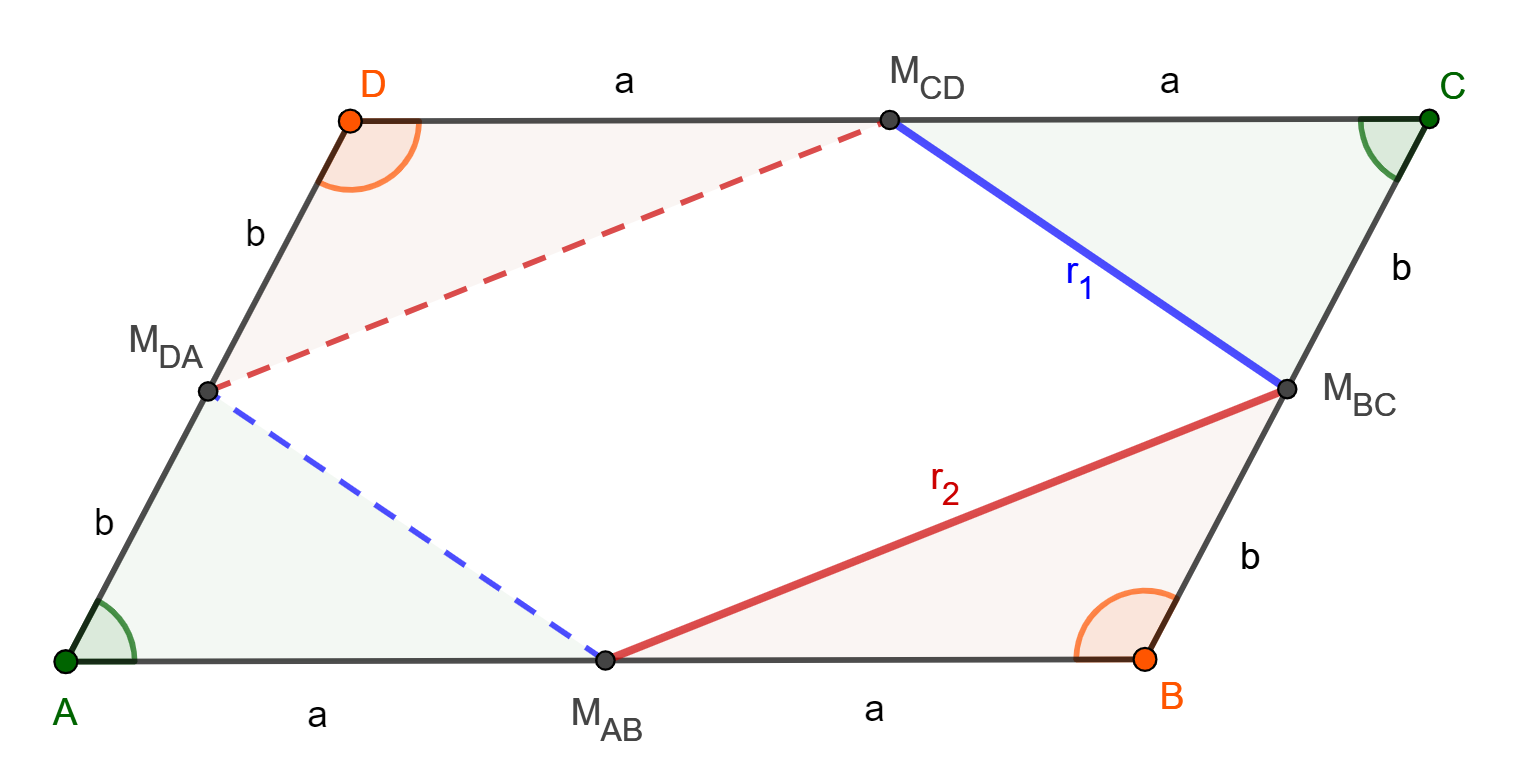
M_{AB}, M_{BC}, M_{CD} a M_{DA} sú stredy strán rovnobežníka ABCD, takže rozdelujú každú stranu na dve polovice, pričom vďaka rovnosti protiľahlých strán, možeme tvrdiť, že:
a = \left|AM_{AB}\right| = \left|M_{AB}B\right| = \left|DM_{CD}\right| = \left|M_{CD}C\right|
b = \left|BM_{BC}\right| = \left|M_{BC}C\right| = \left|DM_{DA}\right| = \left|M_{DA}A\right|
Z vety o zhodnosti dvoch trojuholníkov podľa SUS (strana, uhol, strana) vieme vyhlásiť trojuholníky △M_{DA}AM_{AB} a △M_{BC}CM_{CD} za zhodné a to isté o dvojici trojuholníkov △M_{AB}BM_{BC} a △M_{CD}DM_{DA}. V takom prípade ich tretie strany majú rovnakú dĺžku a r_1 = \left|M_{CD}M_{BC}\right| = \left|M_{DA}M_{AB}\right| zatiaľčo r_2 = \left|M_{AB}M_{BC}\right| = \left|M_{DA}M_{CD}\right|. Nezabúdajme, že stred kružnice k_1 je v M_{AB} a stred kružnice k_2 je v M_{CD}. Obe kružnice so svojím príslušným polomerom budú teda zákonite prechádzať bodom M_{DA}, čím sme dokázali prvú časť úlohy.
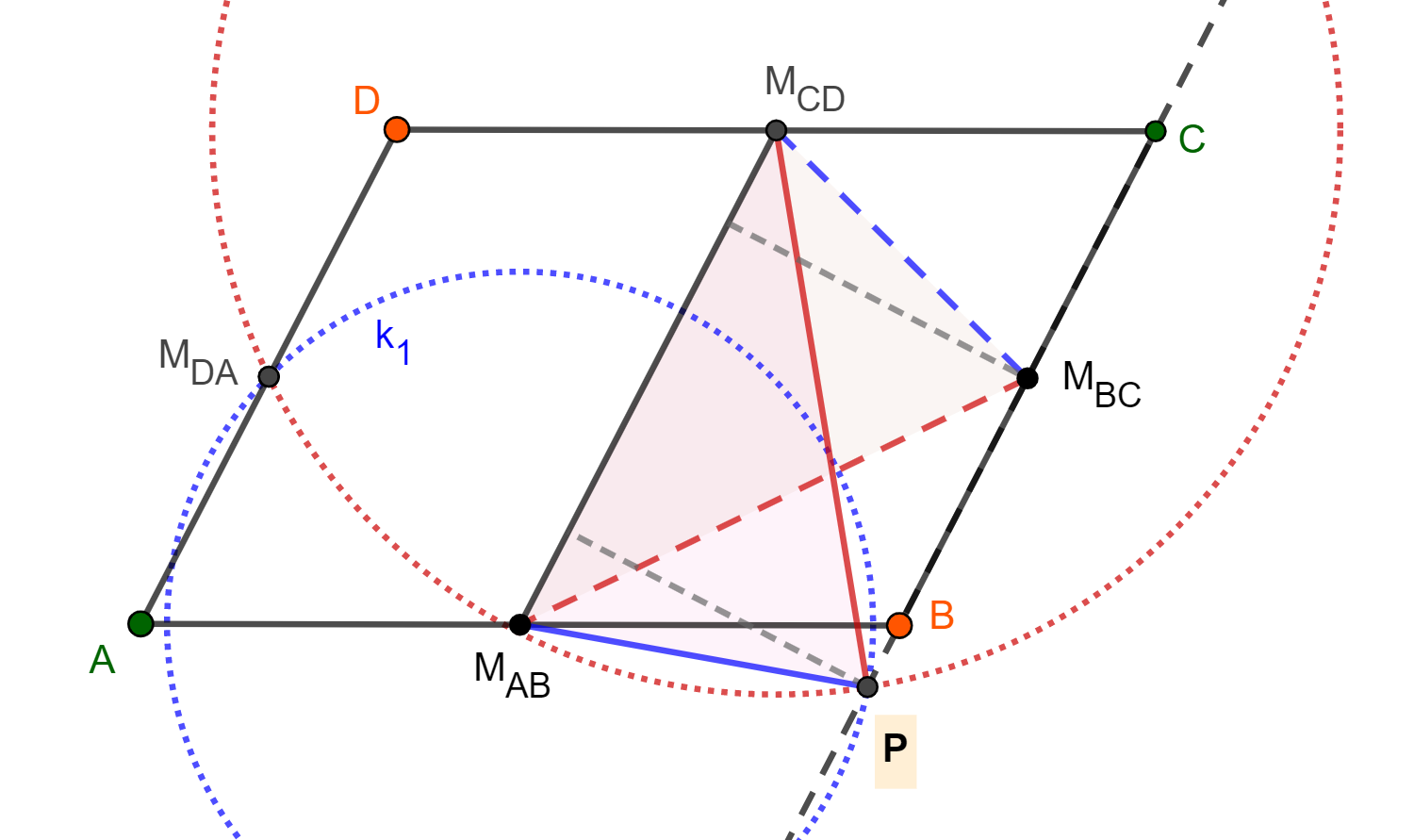
Pozrime sa teraz na druhý priesečník kružníc k_1 a k_2 (pre jednoduchosť si ho označme P). Pri porovnávaní trojuholníkov △M_{AB}M_{CD}P a △M_{AB}M_{CD}M_{BC} si môžeme povšimnúť, že podľa vety o zhodnosti dvoch trojuholníkov podľa SSS (strana, strana, strana), tieto dva trojuholníky sú zhodné, akurát sú zrkadlovo otočené. Ak sa jedna z ich strán zhoduje, tak aj výška na túto stranu bude u oboch trojuholníkov totožná, preto vieme, že výška na stranu M_{AB}M_{CD} u jedného trojuholníku prechádzajúca cez vrchol M_{BC} a u druhého cez vrchol P je rovnaká. Predĺžená priamka M_{AB}M_{CD} sa nachádza rovnobežne ležiaca uprostred priamky AD a priamky BC, kedže M_{AB} aj M_{CD} sa nachádzajú uprostred strán pôvodného rovnobežníka. Ak je teda M_{BC} vzdialený od M_{AB}M_{CD} toľko čo je vzdialená rovnobežka BC ku priamke M_{AB}M_{CD}, tak aj bod P aby bol rovnako vzdialený od M_{AB}M_{CD} musí ležať na priamke BC.
Komentár: Veľa z vás zabudlo na začiatku aspoň zmieniť na základe čoho považujete niečo za zhodné/podobné/rovnobežné/rovnako dlhé/... Spôsobov ako riešiť túto úlohu bolo hneď niekoľko, riešenie ktoré sme tu uviedli bolo jedno z tých častejších. Pre tých, ktorí sa pokúšali využiť pravidlá súmernosti, skúste si oprášiť vedomosti a zopakovať si rozdiel medzi osovou a stredovou súmernosťou.
Určite chceme pochváliť všetkých ktorý si dali záležať na správnom zápise geometrických vzťahov pomocou rovníc alebo na to určených špeciálnych znakov, aspoň tak ako to máme my tu pri rozmeroch a vzdialenostiach úsečiek a strán. Ak si neviete rady s digitálnym kreslením geometrie alebo jednoducho neviete tak presne kresliť, tak odporúčame využiť GeoGebru, ktorá má aj online verziu použiteľnú z webového prehliadača a tak nemusíte nič inštalovať.
Bodovanie: Riešenie úlohy sme rozdelili na dve časti za rovnaký počet bodov, prvá bola dokázať že sa kružnice k_1 a k_2 pretínajú v M_{DA} a druhá časť bola o polohe druhého priesečníku týchto kružníc (dokázať že leží na priamke BC).
8. príklad
Na začiatok bude dobré si uvedomiť, koľko rôznych kariet vlastne obsahuje setový balíček. Keďže každá karta má práve 4 vlastností a každá táto vlastnosť môže nadobúdať tri rôzne stavy, tak celkový počet rôznych kariet vieme vypočítať ako 3^4=81.
Teda vieme, že celkový počet setových kariet je 81. Nás však viac zaujíma, koľko je medzi nimi modrých kariet a koľko rôznych setov z nich vieme vytvoriť. Keďže máme tri rôzne farby, modrých kariet bude presne tretina z celkového počtu, čiže 27.
Teraz sa zamyslime. V akých rôznych setoch môže byť modrá karta? Buď v takých, ktoré obsahujú všetky karty modré alebo všetky majú. rozličnú farbu. Nemôžeme mať teda napríklad set obsahujúci modrú, zelenú a zelenú kartu, lebo by sa porušovalo pravidlo, že majú buď všetky znaky rovnaké alebo všetky rozdielne.
Ďalšie dôležité uvedomenie si je, že ak už sme si určili dve karty, z ktorých chceme vyskladať set, tak tretia karta nám už je jednoznačne daná. Ukážme si to na príklade:
Máme dve kartičky, jedná má na sebe 2 modré vyšrafované štvorce, druhá 2 červené plné štvorce tak ako bude vyzerať tretia? Postupne sa pozrime na vlastnosti akú by mala táto tretia karta spĺňať. Keďže obe kartičky majú rovnaký počet (2) tak aj tretia kartička musí mať počet 2. Prečo? Lebo ak by tam bol iný počet tak by to nebol platný set – neboli by všetky počty rovnaké alebo všetky počty rozdielne. Farba, prvá kartička má modrú farbu, druhá červenú tak aká musí byť tretia farba? Zelená, lebo keď už sa nám v prvých dvoch kartách nezhodujú farby nemôžu sa ani v tretej. Takto podobne zistíme, že výplň musí byť prázdna a tvar musí byť štvorec.
Teraz s týmito poznatkami sa vrhnime do riešenia úlohy.
Rozdeľme si to teda na dva prípady. Najskôr si vypočítame všetky sety, ktoré majú len jednu modrú kartu, a potom všetky sety, ktoré majú všetky karty modré.
Sety ktoré majú len jednu kartu modrú majú na výber z 27 modrých kariet. Potom k tejto modrej karte pridáme nejakú „nemodrú“ čiže jednu z 81-27=54 kariet. Tretia nám už je jednoznačne určená. Takže máme 27\cdot54=1458 setov. Toto však nie je správne riešenie, lebo máme tu všetky sety započítané dvakrát. Ak si označíme kartičky ako A,B,C tak jedna možnosť je, že sme si najprv vybrali A ako modrú kartičku, ako druhú sme si vybrali B a C sme doplnili tak ako bolo spomenuté vyššie. Druhá možnosť je že ako druhú sme si vybrali C a B sme doplnili. Obe možnosti ale dávajú rovnaký set ABC. Takže celkový počet setov s jednou modrou kartou je 27\cdot54\div2=729.
Sety ktoré obsahujú len modrú kartu. Koľkými možnými spôsobmi vieme z 27 kariet urobiť dvojicu (potom tá posledná karta je už jednoznačne určená)? Zvolíme si jednu karitčku a k nej druhú zo zvyšných. Potom výsledok vydelíme 2, keďže na poradí nezáleží. 27\cdot26\div2 = 351. Teraz si už stačí len uvedomiť, že každému setu zodpovedajú tri rôzne výbery 2 kariet. (Majme napríklad set pozostávajúci z kariet A, B a C. Tomuto setu zodpovedajú výbery: AB, AC a BC.) Aby sme dostali celkový počet modrých setov, musíme ešte číslo 351 predeliť tromi, čím dostaneme finálny počet modrých setov 117.
729+117=846
Takže počet platných setov s aspoň jednou modrou kartou je 846.
Iné riešenie:
Využijeme všetky poznatky ktoré sme si povedali, ale dostaneme sa k výsledku s pomocou kombinačných čísel. Koľko je všetkých možných setov? Vyberieme si najskôr jednu dvojicu kariet a tretia nám už je jednoznačne daná. Takže všetkých dvojíc je \displaystyle {81 \choose 2} čo je 3240. Taktiež si musíme uvedomiť, že každému setu zodpovedajú tri rôzne výbery 2 kariet. (Majme napríklad set pozostávajúci z kariet A, B a C. Tomuto setu zodpovedajú výbery: AB, AC a BC.) Takže toto číslo musíme ešte predeliť 3. Takto dostaneme, že všetkých setov je 3240/3=1080.
Čo sú vlastne všetky sety obsahujúce aspoň jednu modrú kartu? Všetky sety bez čisto zelených a čisto červených. Počet len zelených a len červených je pochopiteľne rovnaký ako len modrých, čo sme si ukázali v predošlej časti riešenia čiže 117 možností.
1080-117-117=846
Takže aj za pomoci takéhoto riešenia sme sa dostali k rovnakému výsledku, 846.
Ešte iné riešenie:
Tentokrát sa zvlášť pozrieme na jednotlivé vlastnosti.
Aké počty môžu byť na kartách aby bol set platný?
Jedna možnosť je, že budú všade rovnaké a v tom prípade máme 3 možnosti (všetky 1, všetky 2, všetky 3).
Druhá možnosť je, že budú rôzne a vtedy máme 6 možností toho ktorá karta má ktorý počet (123, 132, 213, 231, 312, 321).
Dokopy teda 9 možností.
Rovnako je to pre tvar a výplň. Pri farbe je to podobne len v prípade, že sú všetky rovnakej farby, musia byť modré a teda tu je len 7 možností.
Všimnime si, že tieto vlastnosti sú na sebe nezávislé a teda celkový počet možností dostaneme tak, že počty možností pre jednotlivé vlastnosti vynásobíme.
9\cdot9\cdot9\cdot7=5103
Toto sa nezhoduje s našimi predchadzajúcimi výsledkami. To znamená, že niečo sme museli započítať navyše. Napríklad možnosti kde sú všetky karty rovnaké. Počet takýchto možností je toľko, koľko je modrých kariet, teda 27.
5103-27=5076
Stále to nevyzerá ako správny výsledok. Problém totiž je, že sme viackrát započítali rovnaké sety. Ak si karty označíme A,B,C tak set ABC sme započítali ako ABC, ACB, BAC, BCA, CAB, CBA, teda šesťkrát. Preto musíme náš výsledok ešte vydeliť 6.
5076/6=846
9. príklad
Podmienka "Žiadne dve čísla nemajú spoločného deliteľa väčšieho ako 1", je veľmi dobrá keď sa na ňu začneme pozerať cez prvočísla. Hovorí totižto, že ak už jedno z pätnástich čísel obsahuje nejaké prvočíslo v prvočíselnom rozklade, tak žiadne iné z našich pätnástich čísel toto prvočíslo v prvočíselnom rozklade mať nebude.
Pozrime sa na nejaké konkrétne číslo m v našej pätnástici. Ak má v prvočíselnom rozklade dve rôzne prvočísla p, q a p < q, tak môžme zapísať m = p \cdot q \cdot z, kde z je nejaké prirodzené číslo. m totižto nemusí byť súčinom len dvoch prvočísel. Vďaka podmienke ale vieme, že žiadne iné číslo v našej pätnástici nie je deliteľné p, pričom p\cdot p < p\cdot q \cdot z, nakoľko p < q \cdot z, keďže z je aspoň 1. To ale znamená, že p\cdot p je tiež číslo od 2 po 2020 a teda naše m ním môžme nahradiť. Takto sme sa teda dostali k tomu, že každé číslo v našej pätnástici môžme zameniť za druhú mocninu najmenšieho prvočísla v ňom a tým dostať novú vyhovujúcu pätnásticu. Keď sa však pozrieme na druhé mocniny prvých pätnástich prvočísel, tak zistíme, že 47^2 = 2209, pričom 47 je pätnáste prvočíslo. To znamená, že ani z prvých pätnástich prvočísel nevieme poskladať vyhovujúcu pätnásticu. To znamená, že nemôže existovať žiadna vyhodujúca pätnástica, nakoľko druhá mocnina ľubovoľného prvočísla väčieho ako 47 by bola viac ako 2209.
Prémia 1
Najlepšie riešenie
Kôpky, ktoré máme pri 130 začneme postupne prehľadávať (zľava doprava). Keďže pre všetky kôpky už máme najhoršie prípady vypísané, tak na mieste kde mi detektor povie áno, sa presunieme nižšie na kôpku s daným počtom nugetiek.
| Počet nugetiek | Počet zlatiek | Rozdelenie na kôpky |
|---|---|---|
| 130 | 17 | 36, 26, 19, 14, 10, 7, 5, 4, 3, 2, 1, 1, 1, 1, 1 |
| 36 | 13 | 10, 7, 5, 4, 3, 2, 1, 1, 1, 1, 1 |
| 26 | 12 | 7, 5, 4, 3, 2, 1, 1, 1, 1, 1 |
| 19 | 11 | 5, 4, 3, 2, 1, 1, 1, 1, 1 |
| 14 | 10 | 4, 3, 2, 1, 1, 1, 1, 1 |
| 10 | 9 | 3, 2, 1, 1, 1, 1, 1 |
| 7 | 8 | 2, 1, 1, 1, 1, 1 |
| 5 | 7 | 1, 1, 1, 1, 1 |
| 4 | 6 | 1, 1, 1, 1 |
| 3 | 5 | 1, 1, 1 |
| 2 | 4 | 1, 1 |
Bodovanie
Body ste dostávali podľa min. počtu potrebných zlatiek nasledovne:- 17 = 8 bodov
- 18 = 7 bodov
- 19 = 6 bodov
- 20 = 5 bodov
- 21 = 4 body
- 22 = 3 body
- 23 - 25 = 2 body
- 26 a viac = 1 bod